平衡二叉樹(AVL樹)
平衡二叉樹簡介:
平衡樹(Balance Tree,BT) 指的是,任意節點的子樹的高度差都小于等于1。常見的符合平衡樹的有,B樹(多路平衡搜尋樹)、AVL樹(二叉平衡搜尋樹)等。
具有以下特點:它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1, 并且左右兩個子樹都是-棵平衡二叉樹。
平衡二叉樹的常用實作方法有紅黑樹、AVL、替罪羊樹、Treap、伸展樹等。可以保證查詢效率高。
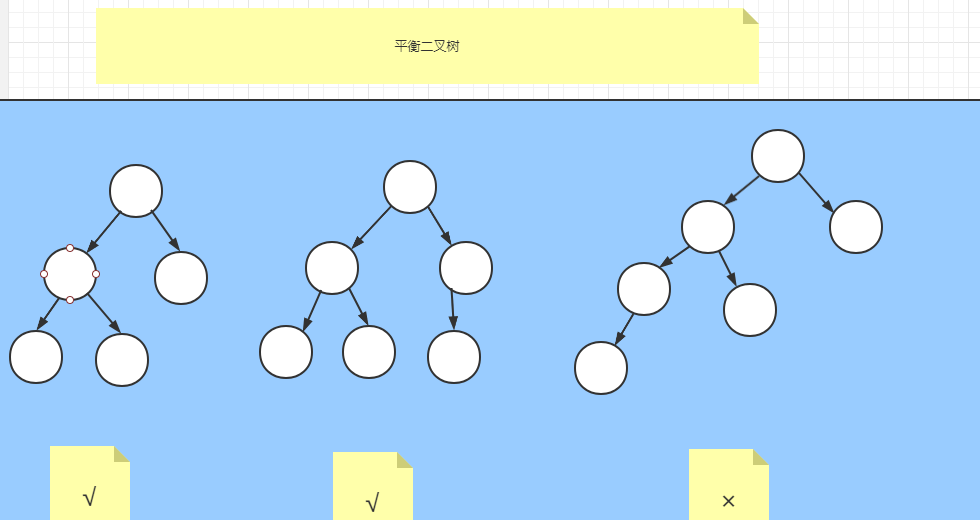
舉例看下下面AVL樹的特點吧:左右兩個子樹的高度差的絕對值不超過1
第三棵樹的左子樹高度是3,右子樹高度是1,3-1=2,是以第三個不是AVL樹
AVL樹左旋
AVL樹左旋圖解
要求: 給你一個數列,建立出對應的平衡二叉樹.數列 {4,3,6,5,7,8}
AVL樹左旋步驟:
- 建立一個新的節點,值為目前節點的值
- 把新節點的的左子樹設定為原節點的左子樹:4-->指向3
- 把新節點的右子樹設定為目前節點的右子樹的左子樹
- 把目前節點的值:4 換成目前右子節點的值:6
- 把目前節點的右子樹設為右子樹的右子樹
- 把目前節點的左子樹設為新的節點:6-->指向4
AVL樹的高度計算
核心:首先要把一棵樹的高度以及左子樹和右子樹的高度計算出來
Node類中添加這三個方法:
1 /**
2 * 傳回以目前節點為根節點的樹的高度
3 *
4 * @return 傳回樹的高度
5 */
6 public int heightTree() {
7 // 比較左子樹跟右子樹的高度,傳回最大的。+1是因為樹本身還要站一層
8 return Math.max(left == null ? 0 : left.heightTree(), right == null ? 0 : right.heightTree()) + 1;
9 }
10
11 /**
12 * 傳回左子樹的高度
13 *
14 * @return 左子樹高度
15 */
16 public int leftHeight() {
17 if (left == null) {
18 return 0;
19 }
20 return left.heightTree();
21 }
22
23 /**
24 * 傳回右子樹的高度
25 *
26 * @return 右子樹高度
27 */
28 public int rightHeight() {
29 if (right == null) {
30 return 0;
31 }
32 return right.heightTree();
33 } View Code
AVLTree類:直接用上個二叉排序樹的樹代碼即可!
1 class AVLTree {
2 private Node root;
3
4 public Node getRoot() {
5 return root;
6 }
7
8 /**
9 * 查找要删除的節點
10 *
11 * @param value
12 * @return
13 */
14 public Node delSearch(int value) {
15 if (root == null) {
16 return null;
17 } else {
18 return root.delSearch(value);
19 }
20 }
21
22 /**
23 * 查找到要删除節點的父節點
24 *
25 * @param value
26 * @return
27 */
28 public Node delSearchParent(int value) {
29 if (root == null) {
30 return null;
31 } else {
32 return root.delSearchParent(value);
33 }
34 }
35
36 /**
37 * 找到最小值并删除
38 *
39 * @param node
40 * @return 傳回删除節點的值
41 */
42 public int delRightTreeMin(Node node) {
43 // 作一個輔助節點
44 Node target = node;
45 // 循環往左子樹進行查找,就會找到最小值
46 while (target.left != null) {
47 target = target.left;
48 }
49 // 删除最小值
50 delNode(target.value);
51 // 傳回最小值
52 return target.value;
53 }
54
55 /**
56 * 删除節點
57 *
58 * @param value
59 */
60 public void delNode(int value) {
61 if (root == null) {
62 return;
63 } else {
64 // 1、找到要删除的節點
65 Node targetNode = delSearch(value);
66 // 沒有找到
67 if (targetNode == null) {
68 return;
69 }
70 // 表示這顆二叉排序樹隻有一個節點(父節點)
71 if (root.left == null && root.right == null) {
72 root = null;
73 return;
74 }
75
76 // 2、找到要删除節點的父節點
77 Node parentNode = delSearchParent(value);
78 // 表示要删除的節點是一個葉子節點
79 if (targetNode.left == null && targetNode.right == null) {
80 // 繼續判斷這個葉子節點是父節點的左子節點還是右子節點
81 if (parentNode.left != null && parentNode.left.value == value) {
82 // 将這個葉子節點置為空
83 parentNode.left = null;
84 } else if (parentNode.right != null && parentNode.right.value == value) {
85 parentNode.right = null;
86 }
87 } else if (targetNode.left != null && targetNode.right != null) {// 删除有兩顆子樹的節點
88 // 找到最小值
89 int minVal = delRightTreeMin(targetNode.right);
90 // 重置
91 targetNode.value = minVal;
92 } else {// 删除隻有一顆子樹的節點
93 if (targetNode.left != null) {// 如果要删除的節點有左子節點
94 if (parentNode != null) {
95 // 待删除節點是父節點的左子節點
96 if (parentNode.left.value == value) {
97 parentNode.left = targetNode.left;
98 } else {// 待删除節點是父節點的右子節點
99 parentNode.right = targetNode.left;
100 }
101 } else {
102 root = targetNode.left;
103 }
104 } else {// 如果要删除的節點有右子節點
105 if (parentNode != null) {
106 // 待删除節點是父節點的左子節點
107 if (parentNode.left.value == value) {
108 parentNode.left = targetNode.right;
109 } else {// 待删除節點是父節點的右子節點
110 parentNode.right = targetNode.right;
111 }
112 } else {
113 root = targetNode.right;
114 }
115 }
116 }
117 }
118 }
119
120 /**
121 * 添加節點的方法
122 *
123 * @param node
124 */
125 public void addNode(Node node) {
126 // root節點為空,就讓root成為根節點
127 if (root == null) {
128 root = node;
129 } else {// root節點不為空,就繼續向樹中添加節點
130 root.addNode(node);
131 }
132 }
133
134 /**
135 * 進行中序周遊
136 */
137 public void infixOrder() {
138 if (root != null) {
139 root.infixOrder();
140 } else {
141 System.out.println("二叉樹為空,無法進行排序!");
142 }
143 }
144 } 測試樹的高度:
public static void main(String[] args) {
int[] arr = {4, 3, 6, 5, 7, 8};
// 建立AVL樹對象
AVLTree avlTree = new AVLTree();
for (int i = 0; i < arr.length; i++) {
// 添加節點
avlTree.addNode(new Node(arr[i]));
}
// 中序周遊
System.out.println("======================中序周遊======================");
avlTree.infixOrder();
System.out.println("======================沒有平衡處理前======================");
System.out.println("沒有平衡處理前樹的高度:" + avlTree.getRoot().heightTree());
System.out.println("沒有平衡處理前樹的左子樹高度:" + avlTree.getRoot().leftHeight());
System.out.println("沒有平衡處理前樹的右子樹高度:" + avlTree.getRoot().rightHeight());
}
附上總體代碼實作:
1 package Demo11_平衡二叉樹_AVL樹;
2
3 /**
4 * @author zhangzhixi
5 * @date 2021/3/12 22:58
6 */
7 public class AVLTreeDemo {
8 public static void main(String[] args) {
9 int[] arr = {4, 3, 6, 5, 7, 8};
10
11 // 建立AVL樹對象
12 AVLTree avlTree = new AVLTree();
13
14 for (int i = 0; i < arr.length; i++) {
15 // 添加節點
16 avlTree.addNode(new Node(arr[i]));
17 }
18
19 // 中序周遊
20 System.out.println("======================中序周遊======================");
21 avlTree.infixOrder();
22 System.out.println("======================沒有平衡處理前======================");
23 System.out.println("沒有平衡處理前樹的高度:" + avlTree.getRoot().heightTree());
24 System.out.println("沒有平衡處理前樹的左子樹高度:" + avlTree.getRoot().leftHeight());
25 System.out.println("沒有平衡處理前樹的右子樹高度:" + avlTree.getRoot().rightHeight());
26 }
27 }
28
29 class AVLTree {
30 private Node root;
31
32 public Node getRoot() {
33 return root;
34 }
35
36 /**
37 * 查找要删除的節點
38 *
39 * @param value
40 * @return
41 */
42 public Node delSearch(int value) {
43 if (root == null) {
44 return null;
45 } else {
46 return root.delSearch(value);
47 }
48 }
49
50 /**
51 * 查找到要删除節點的父節點
52 *
53 * @param value
54 * @return
55 */
56 public Node delSearchParent(int value) {
57 if (root == null) {
58 return null;
59 } else {
60 return root.delSearchParent(value);
61 }
62 }
63
64 /**
65 * 找到最小值并删除
66 *
67 * @param node
68 * @return 傳回删除節點的值
69 */
70 public int delRightTreeMin(Node node) {
71 // 作一個輔助節點
72 Node target = node;
73 // 循環往左子樹進行查找,就會找到最小值
74 while (target.left != null) {
75 target = target.left;
76 }
77 // 删除最小值
78 delNode(target.value);
79 // 傳回最小值
80 return target.value;
81 }
82
83 /**
84 * 删除節點
85 *
86 * @param value
87 */
88 public void delNode(int value) {
89 if (root == null) {
90 return;
91 } else {
92 // 1、找到要删除的節點
93 Node targetNode = delSearch(value);
94 // 沒有找到
95 if (targetNode == null) {
96 return;
97 }
98 // 表示這顆二叉排序樹隻有一個節點(父節點)
99 if (root.left == null && root.right == null) {
100 root = null;
101 return;
102 }
103
104 // 2、找到要删除節點的父節點
105 Node parentNode = delSearchParent(value);
106 // 表示要删除的節點是一個葉子節點
107 if (targetNode.left == null && targetNode.right == null) {
108 // 繼續判斷這個葉子節點是父節點的左子節點還是右子節點
109 if (parentNode.left != null && parentNode.left.value == value) {
110 // 将這個葉子節點置為空
111 parentNode.left = null;
112 } else if (parentNode.right != null && parentNode.right.value == value) {
113 parentNode.right = null;
114 }
115 } else if (targetNode.left != null && targetNode.right != null) {// 删除有兩顆子樹的節點
116 // 找到最小值
117 int minVal = delRightTreeMin(targetNode.right);
118 // 重置
119 targetNode.value = minVal;
120 } else {// 删除隻有一顆子樹的節點
121 if (targetNode.left != null) {// 如果要删除的節點有左子節點
122 if (parentNode != null) {
123 // 待删除節點是父節點的左子節點
124 if (parentNode.left.value == value) {
125 parentNode.left = targetNode.left;
126 } else {// 待删除節點是父節點的右子節點
127 parentNode.right = targetNode.left;
128 }
129 } else {
130 root = targetNode.left;
131 }
132 } else {// 如果要删除的節點有右子節點
133 if (parentNode != null) {
134 // 待删除節點是父節點的左子節點
135 if (parentNode.left.value == value) {
136 parentNode.left = targetNode.right;
137 } else {// 待删除節點是父節點的右子節點
138 parentNode.right = targetNode.right;
139 }
140 } else {
141 root = targetNode.right;
142 }
143 }
144 }
145 }
146 }
147
148 /**
149 * 添加節點的方法
150 *
151 * @param node
152 */
153 public void addNode(Node node) {
154 // root節點為空,就讓root成為根節點
155 if (root == null) {
156 root = node;
157 } else {// root節點不為空,就繼續向樹中添加節點
158 root.addNode(node);
159 }
160 }
161
162 /**
163 * 進行中序周遊
164 */
165 public void infixOrder() {
166 if (root != null) {
167 root.infixOrder();
168 } else {
169 System.out.println("二叉樹為空,無法進行排序!");
170 }
171 }
172 }
173
174 class Node {
175 int value;
176 Node left;
177 Node right;
178
179 public Node(int value) {
180 this.value = value;
181 }
182
183 @Override
184 public String toString() {
185 return "Node{" +
186 "value=" + value +
187 '}';
188 }
189
190 /**
191 * 傳回以目前節點為根節點的樹的高度
192 *
193 * @return 傳回樹的高度
194 */
195 public int heightTree() {
196 // 比較左子樹跟右子樹的高度,傳回最大的。+1是因為樹本身還要站一層
197 return Math.max(left == null ? 0 : left.heightTree(), right == null ? 0 : right.heightTree()) + 1;
198 }
199
200 /**
201 * 傳回左子樹的高度
202 *
203 * @return 左子樹高度
204 */
205 public int leftHeight() {
206 if (left == null) {
207 return 0;
208 }
209 return left.heightTree();
210 }
211
212 /**
213 * 傳回右子樹的高度
214 *
215 * @return 右子樹高度
216 */
217 public int rightHeight() {
218 if (right == null) {
219 return 0;
220 }
221 return right.heightTree();
222 }
223
224 /**
225 * 查找到要删除的節點
226 *
227 * @param value 希望删除節點的值
228 * @return 找到了就傳回這個要删除的節點,沒有找到就傳回null
229 */
230 public Node delSearch(int value) {
231 // 找到的就是要删除的節點
232 if (value == this.value) {
233 return this;
234 } else if (value < this.value) {
235 /**向左子節點查找*/
236 if (this.left == null) {
237 return null;
238 }
239 // 繼續遞歸查找
240 return this.left.delSearch(value);
241 } else {// 要删除節點的值是大于等于目前節點的值
242 if (this.right == null) {
243 return null;
244 }
245 return this.right.delSearch(value);
246 }
247 }
248
249 /**
250 * 查找到要删除節點的父節點
251 *
252 * @param value 要删除的節點的值
253 * @return 找到就傳回要删除節點的父節點,沒有找到就傳回null
254 */
255 public Node delSearchParent(int value) {
256 // 如果目前節點就是要删除的節點的父節點,就傳回
257 if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
258 return this;
259 } else {
260 // 滿足條件表示向左遞歸查找
261 if (this.left != null && value < this.value) {
262 // 向左子樹遞歸找到就傳回
263 return this.left.delSearchParent(value);
264 } else if (this.right != null && value >= this.value) {
265 // 向右子樹遞歸找到就傳回
266 return this.right.delSearchParent(value);
267 } else {
268 // 沒有找到要删除節點的父節點
269 return null;
270 }
271 }
272 }
273
274 /**
275 * 二叉排序樹的添加
276 *
277 * @param node
278 */
279 public void addNode(Node node) {
280 if (node == null) {
281 return;
282 }
283 // 判斷傳進來的節點值與目前節點的關系
284 if (node.value < this.value) {
285 // 左子節點為null
286 if (this.left == null) {
287 this.left = node;
288 } else {
289 // 遞歸的向左子樹添加節點
290 this.left.addNode(node);
291 }
292 } else { // 傳入的節點大于等于目前節點
293 if (this.right == null) {
294 this.right = node;
295 } else {
296 // 遞歸的向右子樹添加節點
297 this.right.addNode(node);
298 }
299 }
300
301 }
302
303 /**
304 * 二叉排序樹的中序周遊
305 */
306 void infixOrder() {
307 if (this.left != null) {
308 this.left.infixOrder();
309 }
310 System.out.println(this);
311 if (this.right != null) {
312 this.right.infixOrder();
313 }
314 }
315 } AVL左旋代碼:
在Node節點中添加AVL樹左旋的方法
/**
* AVL樹左旋轉的方法
*/
public void leftHand() {
// 1.建立新的節點,值為目前節點的值
Node newNode = new Node(this.value);
// 2.把新節點的左子樹設定為原節點的左子樹
newNode.left = this.left;
// 3.把新節點的右子樹設為目前節點的右子樹的左子樹
newNode.right = this.right.left;
// 4.把目前節點的值換成目前節點右子節點的值
this.value = this.right.value;
// 5.把目前節點的右子樹設為右子樹的右子樹
this.right = this.right.right;
// 6.把目前節點的左子樹設定為新的節點
this.left = newNode;
}
在Node節點中添加樹的方法中加入左旋判斷:
1 /**
2 * 二叉排序樹的添加
3 *
4 * @param node
5 */
6 public void addNode(Node node) {
7 if (node == null) {
8 return;
9 }
10 // 判斷傳進來的節點值與目前節點的關系
11 if (node.value < this.value) {
12 // 左子節點為null
13 if (this.left == null) {
14 this.left = node;
15 } else {
16 // 遞歸的向左子樹添加節點
17 this.left.addNode(node);
18 }
19 } else { // 傳入的節點大于等于目前節點
20 if (this.right == null) {
21 this.right = node;
22 } else {
23 // 遞歸的向右子樹添加節點
24 this.right.addNode(node);
25 }
26 }
27 // 當添加完成一個節點後:(右子樹的高度-左子樹的高度)>1,進行左旋操作
28 if (rightHeight() - leftHeight() > 1) {
29 // 進行左旋操作
30 leftHand();
31 }
32 } 測試:
public static void main(String[] args) {
int[] arr = {4, 3, 6, 5, 7, 8};
// 建立AVL樹對象
AVLTree avlTree = new AVLTree();
for (int i = 0; i < arr.length; i++) {
// 添加節點
avlTree.addNode(new Node(arr[i]));
}
// 中序周遊
System.out.println("======================中序周遊======================");
avlTree.infixOrder();
System.out.println("======================AVL樹左旋平衡處理======================");
System.out.println("左旋平衡處理後樹的高度:" + avlTree.getRoot().heightTree());
System.out.println("左旋平衡處理後樹的左子樹高度:" + avlTree.getRoot().leftHeight());
System.out.println("左旋平衡處理後樹的右子樹高度:" + avlTree.getRoot().rightHeight());
}
AVL樹右旋
AVL樹右旋圖解
AVL樹右旋代碼:
在Node類中添加平衡二叉樹右旋代碼:
/**
* AVL樹右旋轉的方法
*/
public void rightHand() {
// 1.建立新的節點,值為目前節點的值
Node newNode = new Node(this.value);
// 2.把新節點的右子樹設定為目前節點的右子樹
newNode.right = this.right;
// 3.把新節點的左子樹設為目前節點的左子樹的右子樹
newNode.left = this.left.right;
// 4.把目前節點的值換成目前節點左子節點的值
this.value = this.left.value;
// 5.把目前節點的左子樹設為左子樹的左子樹
this.left = this.left.left;
// 6.把目前節點的右子樹設定為新的節點
this.right = newNode;
}
在Node類中添加節點時候增加判斷判斷節點應該左旋還是右旋:
1 /**
2 * 二叉排序樹的添加
3 *
4 * @param node
5 */
6 public void addNode(Node node) {
7 if (node == null) {
8 return;
9 }
10 // 判斷傳進來的節點值與目前節點的關系
11 if (node.value < this.value) {
12 // 左子節點為null
13 if (this.left == null) {
14 this.left = node;
15 } else {
16 // 遞歸的向左子樹添加節點
17 this.left.addNode(node);
18 }
19 } else { // 傳入的節點大于等于目前節點
20 if (this.right == null) {
21 this.right = node;
22 } else {
23 // 遞歸的向右子樹添加節點
24 this.right.addNode(node);
25 }
26 }
27 // 當添加完成一個節點後:(右子樹的高度-左子樹的高度)>1,進行左旋操作
28 if (rightHeight() - leftHeight() > 1) {
29 // 進行左旋操作
30 leftHand();
31 }
32 // 當添加完成一個節點後:(左子樹的高度-右子樹的高度)>1,進行右旋操作
33 if (leftHeight() - rightHeight() > 1) {
34 // 進行左旋操作
35 rightHand();
36 }
37 } public static void main(String[] args) {
// 測試左旋轉
//int[] arr = {4, 3, 6, 5, 7, 8};
// 測試右旋轉
int[] arr = {10, 12, 8, 9, 7, 6};
// 建立AVL樹對象
AVLTree avlTree = new AVLTree();
for (int i = 0; i < arr.length; i++) {
// 添加節點
avlTree.addNode(new Node(arr[i]));
}
// 中序周遊
/*System.out.println("======================中序周遊======================");
avlTree.infixOrder();
System.out.println("======================AVL樹左旋平衡處理======================");
System.out.println("左旋平衡處理後樹的高度:" + avlTree.getRoot().heightTree());
System.out.println("左旋平衡處理後樹的左子樹高度:" + avlTree.getRoot().leftHeight());
System.out.println("左旋平衡處理後樹的右子樹高度:" + avlTree.getRoot().rightHeight());*/
System.out.println("======================中序周遊======================");
avlTree.infixOrder();
System.out.println("======================AVL樹右旋平衡處理======================");
System.out.println("右旋平衡處理後樹的高度:" + avlTree.getRoot().heightTree());
System.out.println("右旋平衡處理後樹的左子樹高度:" + avlTree.getRoot().leftHeight());
System.out.println("右旋平衡處理後樹的右子樹高度:" + avlTree.getRoot().rightHeight());
System.out.println("右旋平衡處理後樹的根節點的值:"+avlTree.getRoot().value);
}
AVL樹雙旋
AVL樹雙旋問題以及圖解:
右旋遇到的問題:
前面的兩個數列,進行單旋轉(即一次旋轉)就可以将非平衡二叉樹轉成平衡二叉樹,但是在某些情況下,單旋轉不能完成平衡二叉樹的轉換。
比如數列int[] arr = { 10, 11, 7, 6, 8, 9 }; 運作原來的代碼可以看到,并沒有轉成 AVL 樹.
public static void main(String[] args) {
// 測試左旋轉
//int[] arr = {4, 3, 6, 5, 7, 8};
// 測試右旋轉
//int[] arr = {10, 12, 8, 9, 7, 6};
// 測試旋轉
int[] arr = { 10, 11, 7, 6, 8, 9 };
// 建立AVL樹對象
AVLTree avlTree = new AVLTree();
for (int i = 0; i < arr.length; i++) {
// 添加節點
avlTree.addNode(new Node(arr[i]));
}
// 中序周遊
/*System.out.println("======================中序周遊======================");
avlTree.infixOrder();
System.out.println("======================AVL樹左旋平衡處理======================");
System.out.println("左旋平衡處理後樹的高度:" + avlTree.getRoot().heightTree());
System.out.println("左旋平衡處理後樹的左子樹高度:" + avlTree.getRoot().leftHeight());
System.out.println("左旋平衡處理後樹的右子樹高度:" + avlTree.getRoot().rightHeight());*/
System.out.println("======================中序周遊======================");
avlTree.infixOrder();
System.out.println("======================AVL樹右旋平衡處理======================");
System.out.println("右旋平衡處理後樹的高度:" + avlTree.getRoot().heightTree());
System.out.println("右旋平衡處理後樹的左子樹高度:" + avlTree.getRoot().leftHeight());
System.out.println("右旋平衡處理後樹的右子樹高度:" + avlTree.getRoot().rightHeight());
System.out.println("右旋平衡處理後樹的根節點的值:" + avlTree.getRoot().value);
}
可以發現,将數列進行二叉排序樹後的右旋處理,并沒有變成AVL數:(3 - 1) > 1 是以說不滿足AVL樹
解決思路:
- 當符号右旋轉的條件時
- 如果它的左子樹的右子樹高度大于它的左子樹的高度
- 先對目前這個結點的左節點進行左旋轉
- 在對目前結點進行右旋轉的操作即可
代碼實作:
在添加節點的時候增加判斷,直接上代碼了:
/**
* 二叉排序樹的添加
*
* @param node
*/
public void addNode(Node node) {
if (node == null) {
return;
}
// 判斷傳進來的節點值與目前節點的關系
if (node.value < this.value) {
// 左子節點為null
if (this.left == null) {
this.left = node;
} else {
// 遞歸的向左子樹添加節點
this.left.addNode(node);
}
} else { // 傳入的節點大于等于目前節點
if (this.right == null) {
this.right = node;
} else {
// 遞歸的向右子樹添加節點
this.right.addNode(node);
}
}
// 當添加完成一個節點後:(右子樹的高度-左子樹的高度)>1,進行左旋操作
if (rightHeight() - leftHeight() > 1) {
// 左旋之雙旋判斷
if (this.right != null && this.right.rightHeight() > this.right.rightHeight()) {
// 先對右子結點進行右旋轉
this.right.rightHand();
// 再進行左旋操作
leftHand();
} else {
// 直接進行左旋操作
leftHand();
}
// 右旋判斷: 當添加完成一個節點後:(左子樹的高度-右子樹的高度)>1,進行右旋操作
} else if (leftHeight() - rightHeight() > 1) {
// 右旋之雙旋判斷
if (this.left != null && this.left.rightHeight() > this.left.leftHeight()) {
// 先對目前結點的左結點(左子樹)->左旋轉
this.left.leftHand();
// 再進行右旋操作
rightHand();
} else {
// 直接進行右旋操作
rightHand();
}
}
} package Demo11_平衡二叉樹_AVL樹;
/**
* @author zhangzhixi
* @date 2021/3/12 22:58
*/
public class AVLTreeDemo {
public static void main(String[] args) {
// 測試左旋轉
//int[] arr = {4, 3, 6, 5, 7, 8};
// 測試右旋轉
//int[] arr = {10, 12, 8, 9, 7, 6};
// 測試旋轉
int[] arr = {10, 11, 7, 6, 8, 9};
// 建立AVL樹對象
AVLTree avlTree = new AVLTree();
for (int i = 0; i < arr.length; i++) {
// 添加節點
avlTree.addNode(new Node(arr[i]));
}
// 中序周遊
/*System.out.println("======================中序周遊======================");
avlTree.infixOrder();
System.out.println("======================AVL樹左旋平衡處理======================");
System.out.println("左旋平衡處理後樹的高度:" + avlTree.getRoot().heightTree());
System.out.println("左旋平衡處理後樹的左子樹高度:" + avlTree.getRoot().leftHeight());
System.out.println("左旋平衡處理後樹的右子樹高度:" + avlTree.getRoot().rightHeight());*/
System.out.println("======================中序周遊======================");
avlTree.infixOrder();
System.out.println("======================AVL樹右旋平衡處理======================");
System.out.println("右旋平衡處理後樹的高度:" + avlTree.getRoot().heightTree());
System.out.println("右旋平衡處理後樹的左子樹高度:" + avlTree.getRoot().leftHeight());
System.out.println("右旋平衡處理後樹的右子樹高度:" + avlTree.getRoot().rightHeight());
System.out.println("右旋平衡處理後樹的根節點的值:" + avlTree.getRoot().value);
}
}
class AVLTree {
private Node root;
public Node getRoot() {
return root;
}
/**
* 查找要删除的節點
*
* @param value
* @return
*/
public Node delSearch(int value) {
if (root == null) {
return null;
} else {
return root.delSearch(value);
}
}
/**
* 查找到要删除節點的父節點
*
* @param value
* @return
*/
public Node delSearchParent(int value) {
if (root == null) {
return null;
} else {
return root.delSearchParent(value);
}
}
/**
* 找到最小值并删除
*
* @param node
* @return 傳回删除節點的值
*/
public int delRightTreeMin(Node node) {
// 作一個輔助節點
Node target = node;
// 循環往左子樹進行查找,就會找到最小值
while (target.left != null) {
target = target.left;
}
// 删除最小值
delNode(target.value);
// 傳回最小值
return target.value;
}
/**
* 删除節點
*
* @param value
*/
public void delNode(int value) {
if (root == null) {
return;
} else {
// 1、找到要删除的節點
Node targetNode = delSearch(value);
// 沒有找到
if (targetNode == null) {
return;
}
// 表示這顆二叉排序樹隻有一個節點(父節點)
if (root.left == null && root.right == null) {
root = null;
return;
}
// 2、找到要删除節點的父節點
Node parentNode = delSearchParent(value);
// 表示要删除的節點是一個葉子節點
if (targetNode.left == null && targetNode.right == null) {
// 繼續判斷這個葉子節點是父節點的左子節點還是右子節點
if (parentNode.left != null && parentNode.left.value == value) {
// 将這個葉子節點置為空
parentNode.left = null;
} else if (parentNode.right != null && parentNode.right.value == value) {
parentNode.right = null;
}
} else if (targetNode.left != null && targetNode.right != null) {// 删除有兩顆子樹的節點
// 找到最小值
int minVal = delRightTreeMin(targetNode.right);
// 重置
targetNode.value = minVal;
} else {// 删除隻有一顆子樹的節點
if (targetNode.left != null) {// 如果要删除的節點有左子節點
if (parentNode != null) {
// 待删除節點是父節點的左子節點
if (parentNode.left.value == value) {
parentNode.left = targetNode.left;
} else {// 待删除節點是父節點的右子節點
parentNode.right = targetNode.left;
}
} else {
root = targetNode.left;
}
} else {// 如果要删除的節點有右子節點
if (parentNode != null) {
// 待删除節點是父節點的左子節點
if (parentNode.left.value == value) {
parentNode.left = targetNode.right;
} else {// 待删除節點是父節點的右子節點
parentNode.right = targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
}
/**
* 添加節點的方法
*
* @param node
*/
public void addNode(Node node) {
// root節點為空,就讓root成為根節點
if (root == null) {
root = node;
} else {// root節點不為空,就繼續向樹中添加節點
root.addNode(node);
}
}
/**
* 進行中序周遊
*/
public void infixOrder() {
if (root != null) {
root.infixOrder();
} else {
System.out.println("二叉樹為空,無法進行排序!");
}
}
}
class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node{" +
"value=" + value +
'}';
}
/**
* 傳回以目前節點為根節點的樹的高度
*
* @return 傳回樹的高度
*/
public int heightTree() {
// 比較左子樹跟右子樹的高度,傳回最大的。+1是因為樹本身還要站一層
return Math.max(left == null ? 0 : left.heightTree(), right == null ? 0 : right.heightTree()) + 1;
}
/**
* 傳回左子樹的高度
*
* @return 左子樹高度
*/
public int leftHeight() {
if (left == null) {
return 0;
}
return left.heightTree();
}
/**
* 傳回右子樹的高度
*
* @return 右子樹高度
*/
public int rightHeight() {
if (right == null) {
return 0;
}
return right.heightTree();
}
/**
* 查找到要删除的節點
*
* @param value 希望删除節點的值
* @return 找到了就傳回這個要删除的節點,沒有找到就傳回null
*/
public Node delSearch(int value) {
// 找到的就是要删除的節點
if (value == this.value) {
return this;
} else if (value < this.value) {
/**向左子節點查找*/
if (this.left == null) {
return null;
}
// 繼續遞歸查找
return this.left.delSearch(value);
} else {// 要删除節點的值是大于等于目前節點的值
if (this.right == null) {
return null;
}
return this.right.delSearch(value);
}
}
/**
* 查找到要删除節點的父節點
*
* @param value 要删除的節點的值
* @return 找到就傳回要删除節點的父節點,沒有找到就傳回null
*/
public Node delSearchParent(int value) {
// 如果目前節點就是要删除的節點的父節點,就傳回
if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
return this;
} else {
// 滿足條件表示向左遞歸查找
if (this.left != null && value < this.value) {
// 向左子樹遞歸找到就傳回
return this.left.delSearchParent(value);
} else if (this.right != null && value >= this.value) {
// 向右子樹遞歸找到就傳回
return this.right.delSearchParent(value);
} else {
// 沒有找到要删除節點的父節點
return null;
}
}
}
/**
* 二叉排序樹的添加
*
* @param node
*/
public void addNode(Node node) {
if (node == null) {
return;
}
// 判斷傳進來的節點值與目前節點的關系
if (node.value < this.value) {
// 左子節點為null
if (this.left == null) {
this.left = node;
} else {
// 遞歸的向左子樹添加節點
this.left.addNode(node);
}
} else { // 傳入的節點大于等于目前節點
if (this.right == null) {
this.right = node;
} else {
// 遞歸的向右子樹添加節點
this.right.addNode(node);
}
}
// 當添加完成一個節點後:(右子樹的高度-左子樹的高度)>1,進行左旋操作
if (rightHeight() - leftHeight() > 1) {
// 左旋之雙旋判斷
if (this.right != null && this.right.rightHeight() > this.right.rightHeight()) {
// 先對右子結點進行右旋轉
this.right.rightHand();
// 再進行左旋操作
leftHand();
} else {
// 直接進行左旋操作
leftHand();
}
// 右旋判斷: 當添加完成一個節點後:(左子樹的高度-右子樹的高度)>1,進行右旋操作
} else if (leftHeight() - rightHeight() > 1) {
// 右旋之雙旋判斷
if (this.left != null && this.left.rightHeight() > this.left.leftHeight()) {
// 先對目前結點的左結點(左子樹)->左旋轉
this.left.leftHand();
// 再進行右旋操作
rightHand();
} else {
// 直接進行右旋操作
rightHand();
}
}
}
/**
* 二叉排序樹的中序周遊
*/
void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
/**
* AVL樹左旋轉的方法
*/
public void leftHand() {
// 1.建立新的節點,值為目前節點的值
Node newNode = new Node(this.value);
// 2.把新節點的左子樹設定為目前節點的左子樹
newNode.left = this.left;
// 3.把新節點的右子樹設為目前節點的右子樹的左子樹
newNode.right = this.right.left;
// 4.把目前節點的值換成目前節點右子節點的值
this.value = this.right.value;
// 5.把目前節點的右子樹設為右子樹的右子樹
this.right = this.right.right;
// 6.把目前節點的左子樹設定為新的節點
this.left = newNode;
}
/**
* AVL樹右旋轉的方法
*/
public void rightHand() {
// 1.建立新的節點,值為目前節點的值
Node newNode = new Node(this.value);
// 2.把新節點的右子樹設定為目前節點的右子樹
newNode.right = this.right;
// 3.把新節點的左子樹設為目前節點的左子樹的右子樹
newNode.left = this.left.right;
// 4.把目前節點的值換成目前節點左子節點的值
this.value = this.left.value;
// 5.把目前節點的左子樹設為左子樹的左子樹
this.left = this.left.left;
// 6.把目前節點的右子樹設定為新的節點
this.right = newNode;
}
}