<b>誰更勝一籌?--</b><b>随機搜尋 v.s. </b><b>網格搜尋</b>
我想通過測試來得到自己的答案,我的實驗設定如下。給定空間為(1024,1024)的超參數空間,可由相同形狀的矩陣表示。我們為尋找最佳超參數設定的預算是25個實驗。是以,這将允許我們進行網格搜尋,其中我們設定每個超參數有5個值的組合,或者在該空間中的25個随機搜尋。此外,我設定了一個“批量”版本的随機搜尋,執行5批次每批次5次随機搜尋,優化調整每次批次後的搜尋。生成多個這樣的随機超參數空間後,計算兩種随機搜尋優于網格搜尋的次數。
<b>生成空間</b>
這一步是生成随機2d超參數空間,例如某種地形。
它是一個簡單而優雅的算法。
代碼如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
<b>from</b> <b>__future__</b> <b>import</b> division, print_function
<b>import</b> <b>numpy</b> <b>as</b> <b>np</b>
<b>import</b> <b>matplotlib.pyplot</b> <b>as</b> <b>plt</b>
<b>import</b> <b>matplotlib.cm</b> <b>as</b> <b>cm</b>
<b>import</b> <b>operator</b>
%matplotlib inline
size = 1024
num_iterations = 200
terrain = np.zeros((size, size), dtype="float")
mod_iter =
num_iterations // 10
<b>for</b> iter <b>in</b> range(num_iterations):
<b>if</b> iter % mod_iter == 0:
<b>print</b>("iteration: {:d}".format(iter))
r
= int(np.random.uniform(0, 0.2 * size))
xc, yc = np.random.randint(0, size - 1, 2)
z
= 0
xmin, xmax = int(max(xc - r, 0)), int(min(xc + r,
size))
ymin, ymax = int(max(yc - r, 0)), int(min(yc + r,
<b>for</b> x <b>in</b> range(xmin, xmax):
<b>for</b> y <b>in</b> range(ymin, ymax):
z = (r ** 2) - ((x - xc)
** 2 + (y - yc) ** 2)
<b>if</b> z > 0:
terrain[x, y] += z
<b>print</b>("total
iterations: {:d}".format(iter))
# 标準化單元高度
zmin = np.min(terrain)
terrain -=
zmin
zmax = np.max(terrain)
terrain /=
zmax
terrain = np.power(terrain, 2)
# 乘以255以使地形以灰階表示
terrain =
terrain * 255
terrain.astype("uint8")
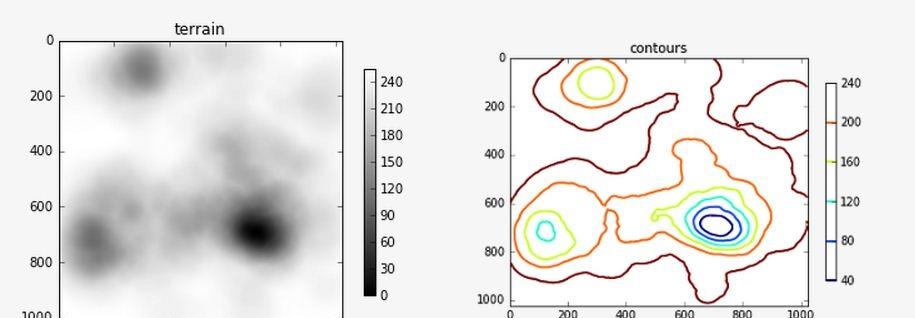
從上面代碼生成的一個可能的地形如下所示。
我還為它生成了一個等高線圖。
1
2
3
4
5
6
7
8
9
plt.title("terrain")
image = plt.imshow(terrain, cmap="gray")
plt.ylim(max(plt.ylim()), min(plt.ylim()))
plt.colorbar(image,
shrink=0.8)
plt.title("contours")
contour = plt.contour(terrain, linewidths=2)
plt.colorbar(contour,
shrink=0.8, extend='both')
<b></b>
網格搜尋
如您所見,地形隻是一個形狀矩陣(1024,1024)。
由于我們的預算是25個實驗,我們将在這個地形上進行一次5x5的網格搜尋。
意即在x和y軸上選擇5個等距點,并讀取這些(x,y)位置處的地形矩陣值。
執行此操作的代碼如下所示。
在輪廓圖上的點的最佳值以藍色标示。
# 執行 (5x5)網格搜尋
results = []
<b>for</b> x <b>in</b> np.linspace(0, size-1, 5):
<b>for</b> y <b>in</b> np.linspace(0, size-1, 5):
xi, yi = int(x), int(y)
results.append([xi, yi, terrain[xi, yi]])
best_xyz = [r <b>for</b> r <b>in</b> sorted(results, key=operator.itemgetter(2))][0]
grid_best =
best_xyz[2]
<b>print</b>(best_xyz)
xvals = [r[0] <b>for</b> r <b>in</b>
results]
yvals = [r[1] <b>for</b> r <b>in</b>
plt.title("grid search")
plt.scatter(xvals,
yvals, color="b", marker="o")
plt.scatter([best_xyz[0]], [best_xyz[1]], color='b', s=200, facecolors='none', edgecolors='b')
plt.colorbar(contour)
<b> </b><b></b>
網格搜尋中最優點坐标為(767,767),值為109。
随機搜尋
接下來進行實驗的是純随機搜尋。由于實驗預設為25個,是以這裡僅随機生成x值和y值,然後在這些點中搜尋地形矩陣值。
# 進行随機搜尋
xvals, yvals, zvals = [], [], []
<b>for</b> i <b>in</b> range(25):
x
= np.random.randint(0, size, 1)[0]
y
results.append((x, y, terrain[x, y]))
best_xyz = sorted(results, key=operator.itemgetter(2))[0]
rand_best = best_xyz[2]
xvals = [r[0] <b>for</b> r <b>in</b> results]
yvals = [r[1] <b>for</b> r <b>in</b> results]
plt.title("random search")
在該測試中,随機搜尋做得更好一些,找到坐标為(663,618)值為103的點。
批量随機搜尋
在這種方法中,我決定将我的25個實驗預算分成5批,每批5個實驗。
查找(x,y)值在每個批次内是随機的。
同時,在每個批次結束時,優勝者會被挑出來進行特殊處理。
采用對象不是在空間中任何地方生成的點,而是在這些點周圍繪制一個視窗,并且僅從這些空間進行采樣。
在每次疊代時,視窗會進行幾何收縮。我試圖尋找到目前為止找到的最優點的鄰域中的點,希望這個搜尋将産生更多的最優點。
同時,我保留剩餘的實驗探索空間,希望我可能找到另一個最佳點。
其代碼如下所示:
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
<b>def</b> cooling_schedule(n, k):
""" 每次運作時減少視窗的大小
n – 批次數目
k – 目前批次的索引号
傳回 乘數(0..1) 的大小
"""
<b>return</b> (n - k) / n
results, winners = [],
[]
<b>for</b> bid <b>in</b> range(5):
<b>print</b>("batch
#: {:d}".format(bid), end="")
# 計算視窗大小
window_size = int(0.25 * cooling_schedule(5,
bid) * size)
# 計算出優勝者并把其值加入結果中
# 隻保持最優的兩點
<b>for</b> x, y, _, _ <b>in</b>
winners:
<b>if</b> x <
size // 2:
# 中左區
xleft = max(x - window_size // 2, 0)
xright = xleft +
window_size
<b>else</b>:
# 中右區
xright = min(x + window_size // 2, size)
xleft = xright -
<b>if</b> y <
# 下半區
ybot = max(y - window_size // 2, 0)
ytop = ybot +
# 上半區
ytop = min(y + window_size // 2, 0)
ybot = ytop -
xnew = np.random.randint(xleft, xright, 1)[0]
ynew = np.random.randint(ybot, ytop, 1)[0]
znew = terrain[xnew, ynew]
results.append((xnew, ynew, znew, bid))
# 添加剩餘随機點
<b>for</b> i <b>in</b> range(5 - len(winners)):
x = np.random.randint(0, size, 1)[0]
y = np.random.randint(0, size, 1)[0]
z = terrain[x, y]
results.append((x, y, z, 2))
# 找出最優兩點
winners = sorted(results, key=operator.itemgetter(2))[0:2]
<b>print</b>("
best: ", winners[0])
plt.title("batched random search")
結束時此空間中的全局最小點坐标(707,682),值為20。
顯然,并不是所有的運作都是如此順利的,也很有可能從上述任何方法發現的點隻是一個局部最小值。
此外,沒有理由假定網格搜尋可能不優于随機搜尋,因為随機地形可能在其中一個均勻布置的點下面具有其全局最小點,并且随機搜尋可能錯過該點。
為了檢查這個假設,我對1000個随機地形批量運作上面的代碼。
對于每個地形,我為3種方法中的每一種運作25個實驗,并為每個方法找到最低(最優)點。我這樣做了兩次,以確定結果的客觀性。代碼如下:
terrain_size = 1024
num_hills = 200
num_trials = 1000
num_searches_per_dim = 5
num_winners = 2
nbr_random_wins = 0
nbr_brand_wins = 0
<b>for</b> i <b>in</b> range(num_trials):
terrain = build_terrain(terrain_size, num_hills)
grid_result = best_grid_search(terrain_size,
num_searches_per_dim)
random_result = best_random_search(terrain_size,
num_searches_per_dim**2)
batch_result = best_batch_random_search(terrain_size,
num_searches_per_dim,
num_searches_per_dim,
num_winners)
<b>print</b>(grid_result, random_result, batch_result)
<b>if</b> random_result <
grid_result:
nbr_random_wins += 1
<b>if</b> batch_result < grid_result:
nbr_brand_wins += 1
<b>print</b>("#
times random search wins: {:d}".format(nbr_random_wins))
times batch random search wins: {:d}".format(nbr_brand_wins))
執行結果如下:
run-1
------
#-times random search wins: 619 ‘随機搜尋優勝次數
run-2
#-times random search wins: 640 ‘随機搜尋優勝次數
#-times batch random search wins: 621随機批量搜尋優勝次數
結果表明随機搜尋似乎比網格搜尋稍好(因為第一個數字超過500)。
此外,批量版本不一定更好,因為純随機搜尋在第二次運作有更好的結果。
<a href="https://promotion.aliyun.com/ntms/act/ambassador/sharetouser.html?usercode=lwju78qa&utm_source=lwju78qa">數十款阿裡雲産品限時折扣中,趕緊點選領劵開始雲上實踐吧!</a>
作者簡介:
sujit pal是一名程式員,在healline
networks擔任技術管理。喜好研究程式設計語言java和python,喜歡從多角度研究和解決問題。
文章原标題《random vs grid search: which
is better?》,作者:sujit pal ,譯者:伍昆