B-tree,B是balance,一般用于資料庫的索引。使用B-tree結構可以顯著減少定位記錄時所經曆的中間過程,進而加快存取速度。而B+tree是B-tree的一個變種,大名鼎鼎的MySQL就普遍使用B+tree實作其索引結構。 那資料庫為什麼使用這種結構? 一般來說,索引本身也很大,不可能全部存儲在記憶體中,是以索引往往以索引檔案的形式存儲的磁盤上。這樣的話,索引查找過程中就要産生磁盤I/O消耗,相對于記憶體存取,I/O存取的消耗要高幾個數量級,是以評價一個資料結構作為索引的優劣最重要的名額就是在查找過程中磁盤I/O操作次數的漸進複雜度。換句話說,索引的結構組織要盡量減少查找過程中磁盤I/O的存取次數。 為了達到這個目的,磁盤按需讀取,要求每次都會預讀的長度一般為頁的整數倍。而且資料庫系統将一個節點的大小設為等于一個頁,這樣每個節點隻需要一次I/O就可以完全載入。每次建立節點時,直接申請一個頁的空間,這樣就保證一個節點實體上也存儲在一個頁裡,加之計算機存儲配置設定都是按頁對齊的,就實作了一個node隻需一次I/O。并把B-tree中的m值設的非常大,就會讓樹的高度降低,有利于一次完全載入。
首先介紹一下m-way查找樹,顧名思義就是一棵樹的每個節點的度小于等于m。
故,它的性質如下:
每個節點的鍵值數小于m
每個節點的度小于等于m
鍵值按順序排列
子樹的鍵值要完全小于或大于或介于父節點之間的鍵值
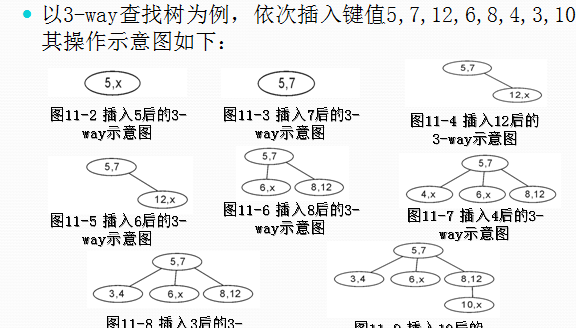
B-tree是一種平衡的m-way查找樹。
B-tree利用多個分支(稱為子樹)的結點,減少擷取記錄時所經曆的結點數,進而達到節省存取時間的目的。
一棵度為m的B-tree應滿足的性質:
每個結點的子結點個數≤m;
根結點若不是葉子結點,它至少有兩個子結點
除根和葉子結點外,每個結點的子結點個數≥ [m/2]
所有的葉子結點都出現在同一層,而且不帶有資訊
非葉子結點若具有j+1個子結點,那麼它包含j個關鍵字(其中,j≤m-1)
B-樹的非葉子結點的結構形式:
ki (1≤i≤j)是關鍵字,所有關鍵字的值是唯一的;pi (0≤i≤j)是指向該結點的子結點的指針
例如圖中的P1,它指向的子樹的關鍵字應該大于k1,小于k2
B-樹的查找
在給定的m階B-樹中查找一個給定值v相等的關鍵字,必須從根結點開始進行查找,一般采用二分查找
B-tree的插入
插入的節點少于M-1個鍵值,則直接插入。
插入的節點的鍵值已等于m-1,則将此節點分為二,因為一棵m的B-tree,最多隻能有m-1個鍵值
B+樹是B-樹的變體。
有幾點不同的地方:
非葉子結點的子樹指針與關鍵字個數相同
為所有葉子結點增加一個鍊指針
所有關鍵字都在葉子結點出現
本文轉自cococo點點部落格園部落格,原文連結:http://www.cnblogs.com/coder2012/p/3330311.html,如需轉載請自行聯系原作者