校驗碼(海明校驗，CRC備援校驗，奇偶校驗)

循環備援校驗碼

CRC碼利用生成多項式為k個資料位産生r個校驗位進行編碼,其編碼長度為n=k+r是以又稱 (n,k)碼. CRC碼廣泛應用于資料通信領域和磁媒體存儲系統中. CRC理論非常複雜,一般書就給個例題,講講方法.現在簡單介紹下它的原理:

在k位資訊碼後接r位校驗碼,對于一個給定的(n,k)碼。可以證明(數學高手自己琢磨證明過程)存在一個最高次幂為 n-k=r 的多項式g(x)，根據g(x)可以生成k位資訊的校驗碼,g(x)被稱為 生成多項式

用C(x)=C(k-1)C(k-2)...C0表示k個資訊位，把C(x)左移r位,就是相當于 C(x)*pow(2,r) 給校驗位空出r個位來了.給定一個 生成多項式g(x),可以求出一個校驗位表達式r(x) 。C(x)*pow(2,r) / g(x) = q(x) + r(x)/g(x) 用C(x)*pow(2,r)去除生成多項式g(x)商為q(x)餘數是r(x)。是以有C(x)*pow(2,r) = q(x)*g(x) + r(x)。

C(x)*pow(2,r) + r(x)就是所求的n位CRC碼,由上式可以看出它是生成多項式g(x)的倍式.是以如果用得到的n位CRC碼去除g(x)如果餘數是0,就證明資料正确. 否則可以根據餘數知道出錯位.

在CRC運算過程中,四則運算采用 mod 2運算(後面介紹),即不考慮進位和借位. 是以上式等價于C(x)*pow(2,r) + r(x) = q(x)*g(x)

繼續前先說下基本概念吧.

1.多項式和二進制編碼

x的最高次幂位對應二進制數的最高位.以下各位對應多項式的各幂次. 有此幂次項為1,無為0. x的最高幂次為r時, 對應的二進制數有r+1位 例如g(x)=pow(x,4) + pow(x,3) + x + 1 對應二進制編碼是 11011

2.生成多項式是發送方和接受方的一個約定,也是一個二進制數,在整個傳輸過程中,這個數不會變.

在發送方利用 生成多項式 對資訊多項式做模2運算生成校驗碼.

在接受方利用 生成多項式 對收到的 編碼多項式 做模2運算校驗和糾錯.

生成多項式應滿足:

a.生成多項式的最高位和最低位必須為1

b.當資訊任何一位發生錯誤時,被生成多項式模2運算後應該使餘數不為0

c.不同位發生錯誤時,應該使餘數不同.

d.對餘數繼續做模2除,應使餘數循環.

生成多項式很複雜，不過不用我們生成。

下面給出一些常用的生成多項式表

n k 二進制碼(自己根據多項式和二進制編碼 的介紹轉)

7 4 1011 或 1101

7 3 11011 或 10111

15 11 1011

31 26 100101

3.模2運算

a.加減法法則

0 +/- 0 = 0

0 +/- 1 = 1

1 +/- 0 = 1

1 +/- 1 = 0

注意:沒有進位和借位

b.乘法法則

利用模2加求部分積之和,沒有進位

c.除法法則

利用模2減求部分餘數，沒有借位，每商1位則部分餘數減1位，餘數最高位是1就商1,不是就商0，當部分餘數的位數小于餘數時,該餘數就是最後餘數.

例 1110 

1011)1100000

1011

1110

1010

0010(每商1位則部分餘數減1位,是以前兩個0寫出)

0000

010(當部分餘數的位數小于餘數時,該餘數就是最後餘數)

最後商是1110餘數是010

　　好了說了那麼多沒用的理論.下面講下CRC的實際應用.例: 給定的生成多項式g(x)=1011, 用(7,4)CRC碼對C(x)=1010進行編碼.

由題目可以知道下列的資訊:

C(x)=1010,n=7,k=4,r=3,g(x)=1011 C(x)*pow(2,3)=1010000 C(x)*pow(2,3) / g(x) = 1001 + 11/1011 是以r(x)=011.是以要求的編碼為1010011

例2: 上題中,資料傳輸後變為1000011,試用糾錯機制糾錯. 1000011 / g(x) = 1011 + 110/1011

不能整除,是以出錯了. 因為餘數是110.查1011出錯位表可以知道是第5位出錯.對其求反即可.

　　備援碼的計算方法是，先将資訊碼後面補0，補0的個數是生成多項式最高次幂；将補零之後的資訊碼除以G(X)，注意除法過程中所用的減法是模2減法，即沒有借位的減法，也就是異或運算。當被除數逐位除完時，得到比除數少一位的餘數。此餘數即為備援位,将其添加在資訊位後便構成CRC碼字。

　　例如，假設資訊碼字為11100011，生成多項式G(X)=X^5+X^4+X+1，計算CRC碼字。

　　G(X) = X^5+X^4+X+1,也就是110011，因為最高次是5，是以，在資訊碼字後補5個0，變為1110001100000。用1110001100000除以110011，餘數為11010，即為所求的備援位。

　　是以發送出去的CRC碼字為原始碼字11100011末尾加上備援位11010，即 1110001111010。接收端收到碼字後，采用同樣的方法驗證，即将收到的碼字除以G(X)，發現餘數是0，則認為碼字在傳輸過程中沒有出錯。

 View Code

奇偶校驗碼

奇偶校驗碼最簡單,但隻能檢測出奇數位出錯. 如果發生偶數位錯誤就無法檢測. 但經研究是奇數位發生錯誤的機率大很多. 而且奇偶校驗碼無法檢測出哪位出錯.是以屬于無法矯正錯誤的校驗碼。奇偶校驗碼是奇校驗碼和偶校驗碼的統稱. 它們都是通過在要校驗的編碼上加一位校驗位組成. 如果是奇校驗加上校驗位後,編碼中1的個數為奇數個。如果是偶校驗加上校驗位後,編碼中1的個數為偶數個。

例:

原編碼 奇校驗 偶校驗

0000   0000 1 0000 0

0010   0010 0 0010 1

1100   1100 1 1100 0

1010   1010 1 1010 0

如果發生奇數個位傳輸出錯,那麼編碼中1的個數就會發生變化. 進而校驗出錯誤，要求從新傳輸資料。目前應用的奇偶校驗碼有3種.

水準奇偶校驗碼對每一個資料的編碼添加校驗位,使資訊位與校驗位處于同一行.

垂直奇偶校驗碼把資料分成若幹組,一組資料排成一行,再加一行校驗碼. 針對每一行列采用奇校驗 或 偶校驗

例: 有32位資料10100101 00110110 11001100 10101011

垂直奇校驗 垂直偶校驗

10100101    10100101    資料

00110110    00110110

11001100    11001100

10101011    10101011

00001011    11110100    校驗

水準垂直奇偶校驗碼就是同時用水準校驗和垂直校驗

奇校驗奇水準  偶校驗 偶水準

 10100101 1     10100101 0   資料

 00110110 1     00110110 0

 11001100 1     11001100 0

 10101011 0     10101011 1

 00001011 0     11110100 1   校驗

 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　海明驗碼

海明碼也是利用奇偶性來校驗資料的. 它是一種多重奇偶校驗檢錯系統,它通過在資料位之間插入k個校驗位,來擴大碼距,進而實作檢錯和糾錯.

設原來資料有n位,要加入k位校驗碼.怎麼确定k的大小呢? k個校驗位可以有pow(2,k) (代表2的k次方) 個編碼,其中有一個代表是否出錯. 剩下pow(2,k)-1個編碼則用來表示到底是哪一位出錯. 因為n個資料位和k個校驗位都可能出錯，是以k滿足pow(2,k)-1 >= n+k。

設 k個校驗碼為 P1,P2...Pk, n個資料位為D0,D1...Dn 産生的海明碼為 H1,H2...H(n+k) 。如有8個資料位,根據pow(2,k)-1 >= n+k可以知道k最小是4。那麼得到的海明碼是：

H12 H11 H10 H9 H8 H7 H6 H5 H4 H3 H2 H1

D7 D6 D5 D4 P4 D3 D2 D1 P3 D0 P2 P1

然後怎麼知道Pi校驗哪個位呢. 自己可以列個校驗關系表

海明碼 下标 校驗位組

H1(P1) 1 P1

H2(P2) 2 P2

H3(D0) 1+2 P1,P2

H4(P3) 4 P3

H5(D1) 1+4 P1,P2

H6(D2) 2+4 P2,P3

H7(D3) 1+2+4 P1,P2,P3

H8(P4) 8 P4

H9(D4) 1+8 P1,P4

H10(D5) 2+8 P2,P4

H11(D6) 1+2+8 P1,P2,P4

H12(D7) 4+8 P3,P4

從表中可以看出

P1校驗 P1,D0,D1,D3,D4,D6

P2校驗 P2,D0,D1,D2,D3,D5,D6

P3校驗 P3,D2,D3,D7

P4校驗 P4,D4,D5,D6,D7

其實上表很有規律很容易記，要知道海明碼Hi由哪些校驗組校驗，可以把i化成二進制數數中哪些位k是1,就有哪些Pk校驗

如H7 7=0111 是以由P1,P2,P3 H11 11=1011 是以由P1,P2,P4 H3 3=0011 是以由P1,P2

那看看Pi的值怎麼确定，如果使用偶校驗,則

P1=D0 xor D1 xor D3 xor D4 xor D6

P2=D0 xor D1 xor D2 xor D3 xor D5 xor D6

P3=D1 xor D2 xor D3 xor D7

P4=D4 xor D5 xor D6 xor D7

其中xor是異或運算，奇校驗的話把偶校驗的值取反即可.那怎麼校驗錯誤呢. 其實也很簡單. 先做下面運算.

G1 = P1 xor D0 xor D1 xor D3 xor D4 xor D6

G2 = P2 xor D0 xor D1 xor D2 xor D3 xor D5 xor D6

G3 = P3 xor D1 xor D2 xor D3 xor D7

G4 = P4 xor D4 xor D5 xor D6 xor D7

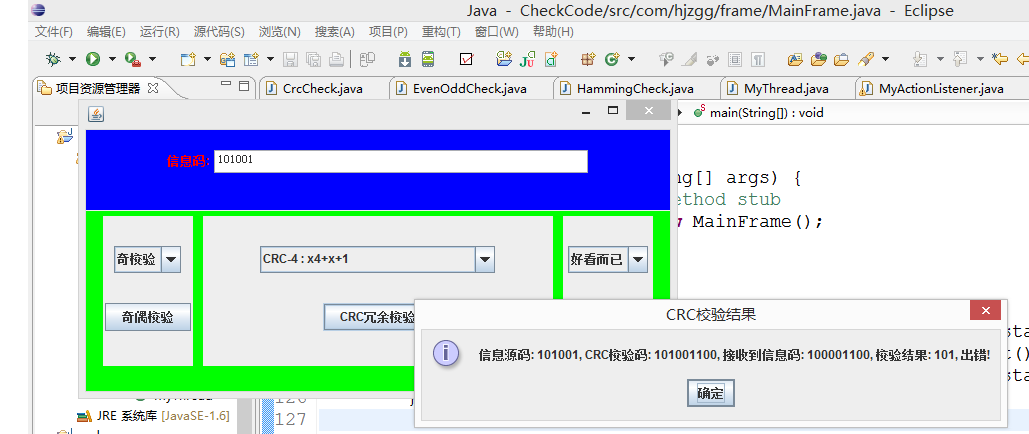
執行程式部分：

　　主程式:

實驗結果: 有圖有真相！

本文轉自 小眼兒 部落格園部落格，原文連結：http://www.cnblogs.com/hujunzheng/p/4858103.html，如需轉載請自行聯系原作者