今天跟大家聊聊最後三種排序: 直接插入排序,希爾排序和歸并排序。
直接插入排序:
這種排序其實蠻好了解的,很現實的例子就是俺們鬥地主,當我們抓到一手亂牌時,我們就要按照大小梳理撲克,30秒後,
撲克梳理完畢,4條3,5條s,哇塞...... 回憶一下,俺們當時是怎麼梳理的。
最左一張牌是3,第二張牌是5,第三張牌又是3,趕緊插到第一張牌後面去,第四張牌又是3,大喜,趕緊插到第二張後面去,
第五張牌又是3,狂喜,哈哈,一門炮就這樣産生了。
怎麼樣,生活中處處都是算法,早已經融入我們的生活和血液。
下面就上圖說明:
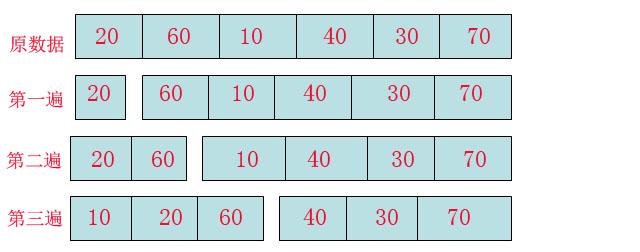
看這張圖不知道大家可否了解了,在插入排序中,數組會被劃分為兩種,“有序數組塊”和“無序數組塊”,
對的,第一遍的時候從”無序數組塊“中提取一個數20作為有序數組塊。
第二遍的時候從”無序數組塊“中提取一個數60有序的放到”有序數組塊中“,也就是20,60。
第三遍的時候同理,不同的是發現10比有序數組的值都小,是以20,60位置後移,騰出一個位置讓10插入。
然後按照這種規律就可以全部插入完畢。
希爾排序:
觀察一下”插入排序“:其實不難發現她有個缺點:
如果當資料是”5, 4, 3, 2, 1“的時候,此時我們将“無序塊”中的記錄插入到“有序塊”時,估計俺們要崩盤,
每次插入都要移動位置,此時插入排序的效率可想而知。
shell根據這個弱點進行了算法改進,融入了一種叫做“縮小增量排序法”的思想,其實也蠻簡單的,不過有點注意的就是:
增量不是亂取,而是有規律可循的。
首先要明确一下增量的取法:
第一次增量的取法為: d=count/2;
第二次增量的取法為: d=(count/2)/2;
最後一直到: d=1;
看上圖觀測的現象為:
d=3時:将40跟50比,因50大,不交換。
将20跟30比,因30大,不交換。
将80跟60比,因60小,交換。
d=2時:将40跟60比,不交換,拿60跟30比交換,此時交換後的30又比前面的40小,又要将40和30交換,如上圖。
将20跟50比,不交換,繼續将50跟80比,不交換。
d=1時:這時就是前面講的插入排序了,不過此時的序列已經差不多有序了,是以給插入排序帶來了很大的性能提高。
既然說“希爾排序”是“插入排序”的改進版,那麼我們就要比一下,在1w個數字中,到底能快多少?
下面進行一下測試:
截圖如下:
看的出來,希爾排序優化了不少,w級别的排序中,相差70幾倍哇。
歸并排序:
個人感覺,我們能容易看的懂的排序基本上都是o (n^2),比較難看懂的基本上都是n(logn),是以歸并排序也是比較難了解的,尤其是在代碼
編寫上,本人就是搞了一下午才搞出來,嘻嘻。
首先看圖:
歸并排序中中兩件事情要做:
第一: “分”, 就是将數組盡可能的分,一直分到原子級别。
第二: “并”,将原子級别的數兩兩合并排序,最後産生結果。
代碼:
結果圖:
ps: 插入排序的時間複雜度為:o(n^2)
希爾排序的時間複雜度為:平均為:o(n^3/2)
最壞: o(n^2)
歸并排序時間複雜度為: o(nlogn)
空間複雜度為: o(n)