平衡樹與AVL
1、二分搜尋樹存在的問題
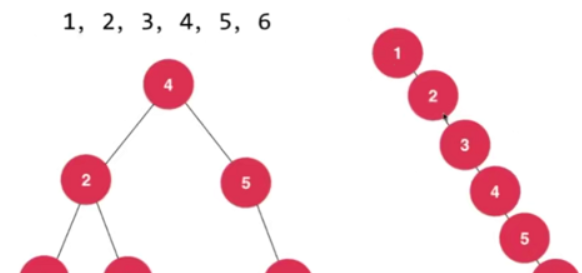
如果資料是順序添加到二分搜尋樹,二分搜尋樹會退化成一個連結清單,這就好大大降低二分搜尋樹的效率。
如何解決這個問題呢?
需要添加一種機制,使得二分搜尋樹維持平衡二叉樹的性質。AVL樹就是一種經典的平衡二叉樹。
2、AVL樹介紹
AVL的名稱來自俄羅斯兩位科學的名字 G.M.Adelson-Velsky和E.M.Landis
1962年的論文首次提出
最早的自平衡二分搜尋樹結構。
3、平衡二叉樹
什麼是平衡二叉樹?
1)、對于任意一個節點,左子樹和右子樹的高度差不能超過1
如下圖所示的平衡二叉樹
12的左子樹高度為3,右子樹高度為2,相差不超過1
8的左子樹高度為2,右子樹高度為1,相差不超過1
18的左子樹高度為1,右子樹高度為0,相差不超過1
2) 平衡二叉樹的高度和節點數量的關系也是O(logn)的
3) 标準節點的高度
4) 計算平衡因子
下圖,黑色數字為高度,藍色數字為平衡因子(左右兩棵樹的高度差)。因為節點12和節點8的左右子樹高度差超過了1,所有不是平衡二叉樹。
一個滿二叉樹一定是平衡二叉樹
完全二叉樹是平衡二叉樹
線段樹是平衡二叉樹
4、平衡二叉樹實作
1) 平衡二叉樹基本定義
基于二分搜尋樹實作,并且Node有key,value和節點的高度。
5、平衡二叉樹(AVL樹)左旋轉和右旋轉
平衡二叉樹是如何實作自平衡的 :左旋轉和右旋轉
什麼時候維護平衡
當插入一個節點時,平衡可能被打破,這時候需要維護平衡
平衡性的破壞反應在這個節點的父親節點和祖先節點上。因為插入的節點後,這個節點的父親節點和祖先節點的高度發生了更新。更新後,平衡因子發生了變化。
加入節點後,沿着節點向上維護平衡性。
如上圖所示,左邊的樹當插入5,節點12的平衡因子為2,打破了平衡。
右邊樹當插入0後,節點8的平衡因子為2,打破了平衡。
右旋轉(RR)
如下圖所示: T1 < z < T2 < x < T3 < y < T4
y節點的平衡因子為2,違法了平衡性
然後進行x.right = y操作
最後進行y.left = T3操作。這樣就變成如下圖所示的樹。這個過程稱為右旋轉。
此時這棵樹即滿足二分搜尋樹的性質,又滿足平衡二叉樹的性質。
有旋轉變化前後分析
假設T1,T2 的最大高度為h,則z為h+1, T3為h+1或者h; x為h+2; T4為h;
修改後,z為h+1不變; T3為h+1或者h; T4為h;y為h+2或者h+1,是以x為h+2或者h+3.
add方法增加rightRotate
左旋轉(LL)
插入的元素在不平衡的節點的右側的右側
T4< y < T3 < x <T1 < z < T2
首先執行x.left = y操作
然後執行x.right=T3
代碼實作:
add方法增加leftRotate
插入的元素在不平衡的節點的左側的右側(LR)
首先對x進行左旋轉。
如下圖所示,轉化為LL(左旋轉)的情況,對y節點進行右旋轉
RL
先對x節點進行右旋轉,如下圖所示,轉化為RR(右旋轉)的情況
完整的代碼如下:
6、平衡二叉樹與二分搜尋樹對比
輸出結果:
準備的資料數量=800000
平衡二叉樹耗時0.828722897秒
二分搜尋樹耗時1.229801731秒
可以看到平衡二叉樹耗時更短。
7、平衡二叉樹的删除