二項分布

二項分布即重複n次獨立的伯努利試驗。在每次試驗中隻有兩種可能的結果，而且兩種結果發生與否互相對立，并且互相獨立，與其它各次試驗結果無關，事件發生與否的機率在每一次獨立試驗中都保持不變，則這一系列試驗總稱為n重伯努利實驗，當試驗次數為1時，二項分布服從0-1分布。

統計學定義

在 機率論和統計學中，二項分布是n個獨立的是/非

試驗中成功的次數的離散 機率分布，其中每次試驗的成功機率為p。這樣的單次成功/失敗試驗又稱為伯努利試驗。實際上，當n = 1時，二項分布就是伯努利分布，二項分布是顯著性差異的二項試驗的基礎。 二項分布 [1]  （Binomial Distribution），即重複n次的 伯努利試驗（Bernoulli Experiment），用ξ表示 随機試驗的結果。

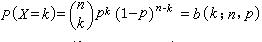
二項分布公式 如果事件發生的 機率是P,則不發生的機率q=1-p，N次 獨立重複試驗中發生K次的機率是 P(ξ=K)= C(n,k) * p^k * (1-p)^(n-k), 其中C(n, k) = n!/(k! * (n-k)!)注意！:第二個等号後面的括号裡的是上标，表示的是方幂。 那麼就說這個屬于二項分布。. 其中P稱為成功機率。 記作ξ~B(n,p)期望：Eξ=np 方差:Dξ=npq 其中q=1-p

二項分布，重複n次出現機率相同的某一事件，出現某種情況的可能機率。

在機率論和統計學中，數學期望(mean)（或均值，亦簡稱期望）是試驗中每次可能結果的機率乘以其結果的總和。是最基本的數學特征之一。它反映随機變量平均取值的大小。

方差（variance)是在機率論和統計方差衡量随機變量或一組資料時離散程度的度量。機率論中方差用來度量随機變量和其數學期望（即均值）之間的偏離程度。統計中的方差（樣本方差）是各個資料分别與其平均數之差的平方的和的平均數。在許多實際問題中，研究方差即偏離程度有着重要意義。

設X是一個 随機變量，若

存在，則稱

為X的方差，記為D(X),Var(X)或DX，其中E(X)指的是對X的預期值，而X是實際值 [1]   。 即

稱為方差，而

稱為标準差 （或 均方差 ）。它與X有相同的量綱。标準差是用來衡量一組資料的離散程度的 統計量 [2]  。 方差刻畫了随機變量的取值對于其數學期望的 離散程度。（标準差、方差越大，離散程度越大。否則，反之) 若X的取值比較集中，則方差D(X)較小,若X的取值比較分散，則方差D(X)較大。 是以，D(X)是刻畫X取值分散程度的一個量，它是衡量取值分散程度的一個尺度。

數學期望展現了随機變量取值的集中位置，他是随機變量的一個重要數字特征，方差展現了随機變量跟其平均值的離散程度。

dbinom(x, size, prob, log = FALSE)# 可用于計算二項= FALSE分布的機率。

pbinom(q, size, prob, lower.tail = TRUE, log.p = FALSE)

qbinom(p, size, prob, lower.tail = TRUE, log.p )

rbinom(n, size, prob)#産生數是獨立實驗成功的次數。

rbinom(n, size, prob)，n代表rbinom函數運作n次，size代表實驗size次，prob是每次運作實驗成功的次數。如果size=1，則是伯努利實驗，産生結果隻能是0或者1.

（該函數，是模拟實驗生成而像分布的滿足要求的x向量的數值）

dbinom(x, size, prob, log = FALSE)# 可用于計算二項= FALSE分布的機率。

##該函數計算

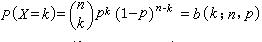
公式p（x=k）的結果，即實驗成功x=k次的機率。

x為實驗成功次數，size為實驗次數。

pbinom(q, size, prob, lower.tail = TRUE, log.p = FALSE)為二項分布的密度累計機率

qbinom(p, size, prob, lower.tail = TRUE, log.p )##是dbinom的逆，求該機率下實驗成功的次數x