C++ 不知圖系列之基于鄰接矩陣實作廣度、深度搜尋

1. 前言

圖是一種抽象資料結構，本質和樹結構是一樣的。

圖與樹相比較，圖具有封閉性，可以把樹結構看成是圖結構的基礎部件。在樹結構中，如果把兄弟節點之間或子節點之間橫向連接配接，便建構成一個圖。

樹适合描述從上向下的一對多的資料結構，如公司的組織結構。

圖适合描述更複雜的多對多資料結構，如群體社交關系、城市交通路線……

本文将讨論以鄰接矩陣方式存儲圖，并在此基礎之上對圖進行深度、廣度搜尋。

2. 圖論

借助計算機解決現實世界中的問題時，除了要存儲現實世界中的資訊，還需要正确地描述資訊之間的關系。

如在開發地圖程式時，除了要存儲城市、街道……等實體資訊，還需要在計算機中描述出城市與城市或城市中各街道之間的連接配接資訊。

在此基礎上，才有可能通過算法計算出從一個城市到另一個城市、或從指定起點到目标點間的最佳路徑。

Tips：類似的還有航班路線圖、火車線路圖、社交關系圖……

圖結構能很好地對現實世界中如上這些資訊以及資訊之間的複雜關系進行映射。以此可使用算法友善的計算出如航班線路中的最短路徑、如火車線路中的最佳中轉方案，如社交圈中誰與誰關系最好、婚姻網中誰與誰最般配……

2.1 圖的概念

頂點：頂點也稱為節點，頂點本身是有資料含義的，都會帶有附加資訊，稱作"有效載荷"。圖中的所有頂點建構成一個頂點集合。是圖的組成部分。

Tips：頂點可以是現實世界中的城市、地名、站名、人……

邊：圖中的邊用來描述頂點之間的關系，圖中所有邊建構成一個邊的集合，是以說，圖包括了頂點集合和邊集合，兩者缺一不可。

邊可以有方向也可以沒有方向，有方向的邊又可分為單向邊和雙向邊。

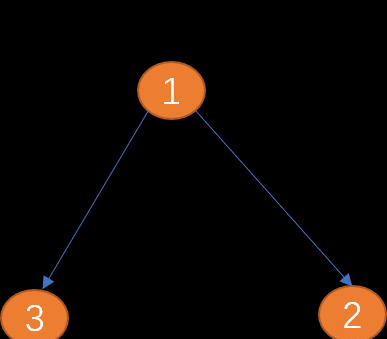
如下圖（頂點1）到（頂點2）之間的邊隻有一方向（箭頭所示為方向），稱為單向邊。類似現實世界中的單向道。（頂點1）到（頂點3）之間的邊有兩個方向（雙向箭頭），稱為雙向邊。城市與城市之間的關系為雙向邊。

權重：邊上可以附加值資訊，附加的值稱為權重。有權重的邊用來描述一個頂點到另一個頂點的連接配接強度。

如現實生活中的地鐵路線中，權重可以描述兩個車站之間時間長度、公裡數、票價……

Tips：邊描述的是頂點之間的關系，權重描述的是連接配接的差異性。

路徑：

先了解現實世界中路徑概念

如：從一個城市開車去另一個城市，就需要先确定好路徑。也就是從出發地到目的地要經過哪些城市？要走多少裡程？

可以說路徑是由邊連接配接的頂點組成的序列。因路徑不隻一條，是以，從一個項點到另一個項點的路徑描述也不隻一種。

在圖結構中如何計算路徑？

無權重路徑的長度是路徑上的邊數。

有權重路徑的長度是路徑上的邊的權重之和。如上圖從（頂點1）到（頂點3）的路徑長度為 8。

環：從起點出發，最後又回到起點（終點也是起點）就會形成一個環，環是一種特殊的路徑。如上圖中的

(V1, V2, V3, V1)

就是一個環。

圖的類型：

綜上所述，圖可以分為如下幾類：

有向圖：邊有方向的圖稱為有向圖。
無向圖：邊沒有方向的圖稱為無向圖。
權重圖：邊上面有權重資訊的圖稱為權重圖。
無環圖：沒有環的圖被稱為無環圖。
有向無環圖：沒有環的有向圖，簡稱 DAG 。

2.2 定義圖

根據圖的特性，圖資料結構中至少要包含兩類資訊：

所有的頂點構成一類集合資訊，這裡用 V 表示（如地圖程式中，所有城市構在頂點集合）。
所有的邊構成一類集合資訊，這裡用 E 表示（城市與城市之間的關系描述）。

如何描述邊？

邊用來表示項點之間的關系。是以一條邊可以包括
3 個中繼資料（起點，終點，權重）。當然，權重是可以省略的，但一般研究圖時，都是指的權重圖。

如果用

表示圖，則

G = (V, E)

。每一條邊可以用二進制組

(fv, ev)

也可以使用三元組

（fv,ev,w）

描述。

fv 表示起點， ev 表示終點。且 fv ， ev 資料必須引用于 V 集合。

如上的圖結構可以描述如下：

# 5 個頂點
V={A0,B1,C2,D3,E4}
# 7 條邊
E={ (A0,B1,3),(B1,C2,4),(C2,D3,6),(C2,E4,1),(D3,E4,2),(A0,D3,5),(E4,B1,7)}

2.3 圖的抽象資料結構

圖的抽象資料描述中至少要有的方法：

Graph ( ) ：用來建立一個新圖。
addertex( vert ) ：向圖中添加一個新節點，參數應該是一個節點類型的對象。
addEdge(fv，tv ) ：在 2 個項點之間建立起邊關系。
addEdge(fv，tv，w ) ：在 2 個項點之間建立起一條邊并指定連接配接權重。
findVertex( key ) : 根據關鍵字 key 在圖中查找頂點。
findVertexs( ) ：查詢所有頂點資訊。
findPath( fv,tv) ：查找從一個頂點到另一個頂點之間的路徑。
……

3. 圖的存儲

圖的存儲實作主流有

種：鄰接矩陣和連結表，本文主要介紹鄰接矩陣。

3.1 鄰接矩陣實作思路

使用一維數組存儲頂點的資訊。

使用二維矩陣（數組）存儲頂點之間的關系。

如

graph[5][5]

可以存儲 5 個頂點的關系資料，行号和列号表示頂點，第 v 行的第 w 列交叉的單元格中的值表示從頂點 v 到頂點 w 的邊的權重，如

grap[2][3]=6

表示

C2

頂點和

D3

頂點的有連接配接（相鄰），權重為

。

鄰接矩陣存儲的優點就是簡單，可以清晰表示那些頂點是相連的。因不是每兩兩個頂點之間會有連接配接，會導緻大量的空間閑置，稱這種矩陣為”稀疏“的。

隻有當每一個頂點和其它頂點都有關系時，矩陣才會填滿。是以，使用這種結構存儲圖資料，對于關系不是很複雜的圖結構而言，會産生大量的空間浪費。可以使用稀疏矩陣壓縮算法減少存儲空間，代價是會增加邏輯關系。

鄰接矩陣适合表示關系複雜的圖結構，如網際網路上網頁之間的連結、社交圈中人與人之間的社會關系……

3.2 編碼實作鄰接矩陣

3.2.1 基本函數

因頂點本身有資料含義，需要先定義頂點類型。

頂點類：

template <typename T>
struct Vertex {
	//頂點的編号
	int verId;
	//頂點的值
	T value;
	//是否被通路過
	bool isVisited;
    //前驅結點編号 
    int preVertexId;
	//無參構造
	Vertex() {
		this->isVisited=false;
        this->preVertexId=0;
	}
	Vertex(int vid) {
		this->verId=vid;
		this->isVisited=false;
        this->preVertexId=0;
	}
	//有參構造
	Vertex(int verId,T value) {
		this->verId=verId;
		this->value=value;
		this->isVisited=false;
        this->preVertexId=0;
	}
	//自我顯示
	void desc() {
		cout<<"頂點編号："<<this->verId<<",結點的值："<<this->value<<"\t";
	}
};

頂點類中

verId

和

value

很好了解。為什麼要添加一個

isVisited

？

這個變量将用來搜尋算法中，用來記錄頂點在路徑搜尋過程中是否已經被搜尋過，避免重複搜尋計算。

圖類：提供對圖的正常維護函數。

#define MAX 11
template <typename T>
class Graph {
	private:
		//一維數組，存儲所有結點,為了友善操作，0 位置不存儲資料
		Vertex<T> verts[MAX];
		//二維數組，用來存儲結點之間的關系，行号和列号為 0 位置不存儲資訊
		int matrix[MAX][MAX];
		//結點編号，從 1 開始
		int num=1;
	public:
		//無參構造，初始化
		Graph() {
			//初始化矩陣的值為 0
			for(int row=0; row<MAX; row++)
				for(int col=0; col<MAX; col++)
					matrix[row][col]=0;
		};
		//添加新結點
		Vertex<T>  addVertex(T value);
		//添加邊
		void addEdge(T from,T to);
		//添加有權重的邊
		void addEdge(T from,T to,int weight);
		//根據結點的編号查找
		Vertex<T> findVertex(int id);
		//根據結點的值查找
		Vertex<T> findVertex(T value);
		//查詢所有結點
		void findAllVertex();
};

3.2.2 實作查詢

查詢結點可以有

種方案：

按結點的值進行查找。這裡使用線性查找算法。

/*
* 根據值查找結點（線性查找算法）
*/
template <typename T>
Vertex<T> Graph<T>::findVertex(T value) {
	for(int i=1; i<MAX; i++) {
		Vertex<T> ver= Graph<T>::verts[i];
		if(ver.value==value)
			return ver ;
	}
	return {0};
}

按結點的編号進行查找。

//根據結點的編号查找結點
template <typename T>
Vertex<T> Graph<T>::findVertex(int id) {
	if(id>=MAX) {
		return {0};
	}
	return Graph::verts[id];
}

3.2.3 添加結點

添加結點時，結點的編号由内部生成，目的是保持編号的連續性。

/*
*添加新結點，并且傳回此結點
*/
template <typename T>
Vertex<T>  Graph<T>::addVertex(T value) {
	//檢查結點是否存在
	Vertex<T> ver= Graph<T>::findVertex(value);
	if(ver.verId==0) {
		//建立新結點,結點編号由内部指定
		ver.verId=Graph<T>::num;
		ver.value=value;
		//存儲
		Graph<T>::verts[Graph<T>::num] =ver;
		Graph<T>::num++;
	}
	return ver;
}

3.2.4 添加結點之間的邊

無權重圖中，結點與結點之間的邊資訊用

表示。有權重圖中，結點與結點之間的邊資訊使用權重表示。

無權重邊的添加：

/*
* 添加頂點與頂點之間的關系
* 無向圖
*/
template <typename T>
void Graph<T>::addEdge(T from,T to) {
	//檢查結點是否存在
	Vertex<T> fromVer=Graph<T>::findVertex(from);
	Vertex<T> toVer=Graph<T>::findVertex(to);
	if(fromVer.verId==0) {
		//不存在，建立此結點
		fromVer=Graph<T>::addVertex(from);
	}
	if(toVer.verId==0)
		toVer=Graph<T>::addVertex(to);
	//無向圖中，可以單向描述，也可以雙向描述
	Graph<T>::matrix[fromVer.verId][toVer.verId]=1;
	//雙向描述
	Graph<T>::matrix[toVer.verId][fromVer.verId]=1;
}

有權重邊的添加：

/*
*添加頂點與頂點之間的關系
*有向權重圖
*/
template <typename T>
void Graph<T>::addEdge(T from,T to,int weight) {
	//檢查結點是否存在
	Vertex<T> fromVer=Graph<T>::findVertex(from);
	Vertex<T> toVer=Graph<T>::findVertex(to);
	if(fromVer.verId==0) {
		//不存在，建立此結點
		fromVer=Graph<T>::addVertex(from);
	}
	if(toVer.verId==0)
		toVer=Graph<T>::addVertex(to);
	//有向權重圖
	Graph<T>::matrix[fromVer.verId][toVer.verId]=weight;
}

3.2.3 查詢所有結點

周遊圖時，除了顯示結點自身資訊，同時顯示與結點有關的邊的資訊。

//查詢所有結點
template <typename T>
void Graph<T>::findAllVertex() {
	for(int i=1; i<Graph<T>::num; i++) {
		Vertex<T> ver= Graph::verts[i];
		ver.desc();
		cout<<endl;
		//查找與此結點有關系的結點
		for(int col=1; col<MAX; col++) {
			int weight=Graph::matrix[ver.verId][col];
			if(weight!=0) {
				//找到結點
				Vertex<T> ver_= Graph::findVertex(col);
				cout<<"\t";
				ver_.desc();
				cout<<"權重："<<weight<<endl;
			}
		}
	}
}

3.2.4 測試

int main(int argc, char** argv) {
	//建立圖執行個體
	Graph<char> graph;
	//添加 A（編号1），B（編号2），C（編号3），D（編号4），E （編号5）  5個結點
	char verInfos[5]= {'A','B','C','D','E'};
	for(int i=1; i<=5; i++) {
		graph.addVertex(verInfos[i-1]);
	}
	cout<<"圖中的結點"<<endl;
	graph.findAllVertex();
	//添加結點之間的關系 (A,B,3),(A,D,5),(B,C,4),(C,D,6),(C,E,1),  (D,E,2),(E,B,7)
	graph.addEdge('A','B',3);
	graph.addEdge('A','D',5);
	graph.addEdge('B','C',4);
	graph.addEdge('C','D',6);
	graph.addEdge('C','E',1);
	graph.addEdge('D','E',2);
	graph.addEdge('E','B',7);
	cout<<"結點之間的關系："<<endl; 
	graph.findAllVertex();
	return 0;
}

測試輸出結果：

4. 搜尋路徑

在圖中經常做的操作，就是查找從一個頂點到另一個頂點的路徑。

什麼是路徑？

無權圖中，路徑指從一個頂點到另一個頂點經過邊的數量。

有權圖中，路徑指從一個頂點到另一個頂點經過的所有邊上權重相加之和。

如查找到

A1

到

E5

之間的路徑長度：

直覺思維角度查找一下，可以找到如下路徑以及路徑長度。

{A1，B2，C3，E5} 路徑長度為 8 。
{A1，D4，E5} 路徑長度為 7 。
{A1，B2，C3，D4，E5} 路徑長度為 15 。

人的思維是知識性、直覺性思維，在路徑查找時不存在所謂的嘗試或碰壁問題。而計算機是試探性思維，就會出現這條路不通，再找另一條路的現象。

是以最短路徑算法中常常會以錯誤為代價，在查找過程中會走一些彎路。常用的路徑搜尋算法有

種：

廣度優先搜尋。
深度優先搜尋。

4.1 廣度優先搜尋

看一下廣度優先如何周遊圖上所有結點：

廣度優先搜尋的基本思路：

确定出發點，如上圖是 A1 頂點。
以出發點相鄰的頂點為候選點，并存儲至隊列（已經存儲過的頂點不用再存儲）。
從隊列中每拿出一個頂點後，再把與此頂點相鄰的其它頂點做為候選點存儲于隊列。
不停重複上述過程，直到找到目标頂點或隊列為空。

基礎版的廣度優先搜尋算法隻能保證找到路徑，而不能儲存找到最佳（短）路徑。如上圖如果要從

A1

搜尋到

E5

中間需要經過

B2->D4->C3

頂點。

編碼實作廣度優先搜尋：

廣度優先搜尋需要借助隊列臨時存儲選節點，本文使用

STL

中的隊列，在檔案頭要添加下面的包含頭檔案:

#include <queue>
#include <stack>

在圖類中實作提供廣度優先搜尋算法的函數。

class Graph():
	private:
        //……
     public:
        //廣度算法查找 from 頂點到 to 頂點的搜尋路徑
	   void bfs(T  from ,T to); 
	   void findNeighbor(queue<Vertex<T>> &myQueue, Vertex<T> & ver );

廣度優先搜尋過程中，需要随時擷取與目前節點相鄰的節點，

findNeighbor()

方法的作用就是用來把目前節點的相鄰節點壓入隊列中。

//輔助函數，查找結點的鄰接結點
template <typename T>
void Graph<T>::findNeighbor(queue<Vertex<T>>  &myQueue, Vertex<T> & ver ) {
	for(int col=1; col<MAX; col++) {
		if( Graph<T>::matrix[ver.verId][col]!=0 ) {
			//相鄰結點
			Vertex<T> nv= Graph<T>::findVertex(col);
			//壓入隊列
			if(nv.isVisited==false) {
                 //指定前驅結點編号
				nv.preVertexId=ver.verId;
                 //設定結點已經被壓入過隊列中
				nv.isVisited=true;
                 //修改結點
				Graph<T>::verts[col]=nv;
				myQueue.push(nv);
			}
		}
	}
}

廣度優先搜尋算法：

//廣度搜尋
template <typename T>
void Graph<T>::bfs(T  from ,T to) {
	//儲存搜尋到的路徑
	stack< Vertex<T>> paths;
	//隊列
	queue<Vertex<T>> myQueue;
	//檢查結點是否存在
	Vertex<T> fromVer=Graph<T>::findVertex(from);
	Vertex<T> toVer=Graph<T>::findVertex(to);
	if(fromVer.verId==0 || toVer.verId==0)
		//不存在
		return ;
	//把起始頂點壓入隊列
	myQueue.push(fromVer);
    cout<<"廣度搜尋結點順序："<<"\t"; 
	while(!myQueue.empty()) {
		//從隊列中得到頂點
		Vertex<T> top= myQueue.front();
        cout<<top.value<<"\t";
		myQueue.pop();
		if(top.verId==toVer.verId && top.value==toVer.value) {
			//找到目标頂點後，順着前驅向上存儲
			Vertex<T> move=top;
			int weight=0;
			while(move.preVertexId!=0) {
				paths.push(move);
				//找到前驅
				move=Graph<T>::findVertex(move.preVertexId);
				weight+=Graph<T>::matrix[move.verId][paths.top().verId];
			}
			paths.push(fromVer);
			cout<<"\n頂點"<<fromVer.value<<"-"<<"項點"<<toVer.value<<"的路徑：("<<weight<<")";
             //輸出路徑，不一定是最短路徑
			while(!paths.empty()) {
				Vertex<T> v= paths.top();
				v.desc();
				paths.pop();
			}
			break;
		} else
             //查找相鄰頂點
			Graph<T>::findNeighbor(myQueue,top);
	}
}

測試廣度優先搜尋算法：

int main(int argc, char** argv) {
	//省略其它代碼
    //廣度搜尋
	graph.bfs('A','E');
	return 0;
}

輸出結果：

4.2 深度優先搜尋算法

先看一下如何使用深度優先算法周遊圖中所有結點。

深度優先搜尋算法與廣度優先搜尋算法不同之處：候選節點是放在棧中的。這也決定了兩者的本質差別：廣度是先進先出的搜尋順序、深度是先進後出的搜尋順序。

使用廣度和深度搜尋周遊圖時，最後搜尋到結點的順序是不相同的：

廣度周遊順序： A1->B2->D4->C3->E5 。
深度周遊順序： A1->D4->E5->B2->C3 。

使用循環實作深度優先搜尋算法：

在圖類中添加如下函數：

class Graph():
	private:
        //……
     public:
        //深度搜尋查找 from 頂點到 to 頂點的路徑 
	   void dfs(T  from ,T to); 
	   void findNeighbor(stack<Vertex<T>> &myStack, Vertex<T> & ver );

深度優先搜尋算法：

template <typename T>
void Graph<T>::findNeighbor(stack<Vertex<T>> &myStack, Vertex<T> & ver ) {
	for(int col=1; col<MAX; col++) {
		if( Graph<T>::matrix[ver.verId][col]!=0 ) {
			//相鄰結點
			Vertex<T> nv= Graph<T>::findVertex(col);
			//壓入棧隊
			if(nv.isVisited==false) {
				nv.preVertexId=ver.verId;
				nv.isVisited=true;
				Graph<T>::verts[col]=nv;
				myStack.push(nv);
			}
		}
	}
}
//深度搜尋查找 from 頂點到 to 頂點的路徑
template <typename T>
void Graph<T>::dfs(T  from ,T to) {
	//儲存搜尋到的路徑
	stack< Vertex<T>> paths;
	//隊列
	stack<Vertex<T>> myStack;
	//檢查結點是否存在
	Vertex<T> fromVer=Graph<T>::findVertex(from);
	Vertex<T> toVer=Graph<T>::findVertex(to);
	if(fromVer.verId==0 || toVer.verId==0 ) return;
	//把起始頂點壓入棧
	myStack.push(fromVer);
    cout<<"深度搜尋結點順序："<<"\t"; 
	while(!myStack.empty()) {
		//從棧中得到頂點
		Vertex<T> top= myStack.top();
        cout<<top.value<<"\t";
		myStack.pop();
		if(top.verId==toVer.verId && top.value==toVer.value) {
			//找到
			Vertex<T> move=top;
			int weight=0;
			while(move.preVertexId!=0) {
				paths.push(move);
				move=Graph<T>::findVertex(move.preVertexId);
				weight+=Graph<T>::matrix[move.verId][paths.top().verId];
			}
			paths.push(fromVer);
			cout<<"\n頂點"<<fromVer.value<<"-"<<"項點"<<toVer.value<<"的路徑：("<<weight<<")";
			while(!paths.empty()) {
				Vertex<T> v= paths.top();
				v.desc();
				paths.pop();
			}
			break;
		} else
			Graph<T>::findNeighbor(myStack,top);
	}
}

深度搜尋測試：

int main(int argc, char** argv) {
	//省略其它代碼
    //深度搜尋
	graph.dfs('A','E');
	return 0;
}

輸出結果：

C++ 不知圖系列之基于鄰接矩陣實作廣度、深度搜尋

1. 前言

2. 圖論

2.1 圖的概念

2.2 定義圖

2.3 圖的抽象資料結構

3. 圖的存儲

3.1 鄰接矩陣實作思路

3.2 編碼實作鄰接矩陣

3.2.1 基本函數

3.2.2 實作查詢

3.2.3 添加結點

3.2.4 添加結點之間的邊

3.2.3 查詢所有結點

3.2.4 測試

4. 搜尋路徑

4.1 廣度優先搜尋

4.2 深度優先搜尋算法

5. 總結

繼續閱讀

關于在 xmlSPY 出現的錯誤 DOCTYPE-EXternalID的名稱必須既是SYSTEM 又是PUBLIC?(轉)

Matplotllib——繪制複雜函數圖與三維圖

尚矽谷java入門356p-379p 面向對象和異常 2022.3.22

NLP中如何有效應用異常檢測？

拓端資料tecdat|R語言樣條曲線、決策樹、Adaboost、梯度提升(GBM)算法進行回歸、分類和動态可視化

複現經典：《統計學習方法》第 8 章提升方法

CodeForces - 986A Fair

2.2019-11-19ubunt環境準備及k8s安裝環境準備

Cesium左鍵點選模型效果分析

Docker：可視化管理工具Portainer與分析建立管理者賬号錯誤的原因

Docker - Docker Container及Container指令詳解

POJ 1276 Cash Machine

D3.js學習筆記(1)

pycharm 2019.2.1 注冊方法

Java并發程式設計一ReentrantReadWriteLock初使用

【FPGA實作GA】基于FPGA的GA優化算法的設計與實作