Projection
Until now,we have described our objects and eye in 3 dimensions,Our next step is to understand how to turn into a 2D image as would be seen from eye. To do this we will need to model a simple camera, Throughout, we will assume that the camera is placed at original of eye frame
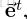
and that it is looking down the eye's negative z-axis.We will use the notation
to refer to eye coordinate of point.
直到現在,我們已經在3D空間中描述了物體及視角的位置。下一步我們将要把這個3D空間變換到一張2D圖檔上。為了達到這一點,我們需要放置一個簡單的相機。至始至終,将假定相機被放置在視空間(
)的原點。朝向視空間-Z方向,使用
表示視空間的一個點。
10.1 針孔相機:(PinHole Camera)
The simplest possible camera is a pinhole camera(see Figure 10.1).As Light tralvels towards the film plane,most is blocked by an opaque surface placed at
plane. But we place a very small hole in the center of the surface, at the point with eye coordinate
Only rays of light that pass through this point reach the film plane and have their intensity recorded on film. The image is reocord at film plane placed at ,say,
針孔相機可能是最簡單的相機,當光射向膠片平面時,大部分光背放置在原點處的一個平面擋住了。但是,如果我們放置一個小洞在原點處。那些透過的光就能被放置在1處的膠片平面記錄到。
為了得到正确的圖像(無需反轉),計算時把膠片平面放置在了相機的前面
Once the picutre has been created,if we hold up photograph at the
plane,and
observe it with our own eye placed at origin(see Figure10.3),it will look to us just like the original scene would have.We are exactly reproducing the data that would have reached our eye if we had stood there and looked at the scene. if we move the picture around in space,say colser or farther from our eye,we will no longer be exactly reproducing the original scene-stimulus,but it will appear like a reasonably valid visual representation of orginal scene.
本段未能了解
10.3 Variations
By changing the entries in the projection matrix we can slightly alter the geometry of the camera transformation.
通過改變投影矩陣的元素,我們可以稍微的改變投影矩陣的幾何結構。
10.3.1 Scales
In computer graphics this non-uniformity is useful when dealing with non-square windows on the screen,Suppose the window is wider than it is high. In our camera transform ,we need to squish things horizontally so a wider horizontal field of view fits into retained canonical. when the data is later mapped to the window,it will be stretched out corresponding and will not appear distorted.
10.3.2 Shifts
該部分主要考慮的是是椎體左右上下不是完全對稱的情況,事實上,該部分的内容更具有廣泛的适用性