最大堆和最小堆

堆的特性

• 必須是完全二叉樹
• 用數組實作
• 任一結點的值是其子樹所有結點的最大值或最小值
  • 最大值時，稱為“最大堆”，也稱大頂堆；
  • 最小值時，稱為“最小堆”，也稱小頂堆。

最大堆:

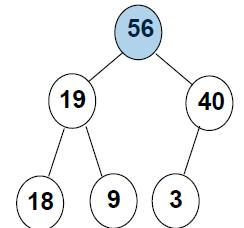
最小堆：

• 對于堆（Heap）這種資料結構，從根節點到任意結點路徑上所有的結點都是有序的

堆的實作

在堆中，一般将數組第一個元素指派為null，不用數組第一位，是以

• 根節點：n
• 左子樹則為：2*n
• 右子樹則為：2*n+1
• 對于任一結點n,其父結點為n/2 取整即可。

基于數組實作堆

//基于數組實作的完全二叉樹
    //如果結點值為n,那麼其左子樹則為2n,右子樹為2n+1；對于任一結點n,其父結點為n/2 取整即可。
    List<Integer> list;

    public MaxHeap() {
        //基于數組實作
        list = new ArrayList<>();
        //數組首位為null，使得數組從下标為1的位置開始，
        // 這樣，完全二叉樹中，如果結點值為n,那麼其左子樹則為2n,右子樹為2n+1
        list.add(0, null);
    }
           

最大堆

所謂最大堆，就是數組中最大的元素位于樹的根節點位置，父節點大于子節點，但是，左右子節點大小與左子樹還是右子樹無關

建構最大堆：

• 插入新元素到完全二叉樹最右子節點即數組尾部
• 上濾
• 不斷上濾交換位置，完成插入

何為上濾？

上濾：是将子節點和父節點進行比較，根據條件交換子節點和父節點

• 在最大堆中：如果子節點比父節點大，則交換，将大的元素上升上去
• 在最小堆中：如果子節點比父節點小，則交換，将小的元素升上去

建構最大堆

/**
     * <h>插入堆</h>
     * <li>1. 插入到完全二叉樹的右子樹</li>
     * <li>2. 上濾：和父節點比較，比父節點大則交換位置</li>
     * <li>3. 不斷交換，完成插入</li>
     *
     * @param x
     */
    public void insert(int x) {

        //插入到數組末，相當于插入到完全二叉樹的最右子樹
        list.add(x);
        //獲得目前插入節點的數組下标,是從 1 開始計
        int index = list.size() - 1;
        //該節點的父節點下标
        int pIndex = index / 2;
        //上濾
        while (index > 1) {
            //最大堆：如果目前節點比父節點值要大，則交換
            if (x > list.get(pIndex)) {
                list.set(index, list.get(pIndex));
                index = pIndex;
                //下一個父節點
                pIndex = index / 2;
            } else {
                //小則不用調整
                break;
            }
        }
        // 最終找到index 的位置，把值放進去
        list.set(index, x);
    }
           

最小堆

所謂最小堆，就是數組中最小的元素在樹的根節點，跟最大堆相反

建構最小堆：

• 插入新元素到完全二叉樹最右子節點即數組尾部
• 上濾
• 不斷上濾交換位置，完成插入

最大堆和最小堆的上濾條件是不一樣的，上文也有提到

public void insert(int x) {
        //添加到數組尾部
        list.add(x);
        //獲得目前插入節點的數組下标,是從 1 開始計
        int index = list.size() - 1;
        //該節點的父節點下标
        int pIndex = index / 2;
        //上濾
        while (index > 1) {
            //跟父節點比較
            if (list.get(pIndex) > x) {
                //比父節點小，交換
                list.set(index, list.get(pIndex));
                index = pIndex;
                pIndex = pIndex / 2;
            } else {
                break;
            }
        }
        //找到位置，指派
        list.set(index, x);
    }
           

删除元素

移除堆中元素：

• 找到要删除的元素
• 将數組末端元素即最右子節點元素和其交換
• 下濾

何為下濾？

下濾：是将子節點和父節點進行比較，根據條件交換子節點和父節點

• 在最大堆中：如果子節點比父節點小，則交換，将小的元素下降下去
• 在最小堆中：如果子節點比父節點小，則交換，将小的元素降下來

最大堆中删除元素

/**
     * 移除堆中節點
     *
     * @param x
     */
    public void delete(int x) {
        //判斷堆是否為空堆
        if (list.isEmpty()) {
            return;
        }
        //擷取該元素下标
        int index = list.indexOf(x);
        //沒有該元素
        if (index == -1) {
            return;
        }
        //獲得數組最後一個元素下标，即完全二叉樹中最右子樹的下标
        int tmp = list.size() - 1;
        //将要删除的x和tmp交換位置，即用最後一個元素替換被删除的位置
        list.set(index, list.get(tmp));
        //下濾
        //父節點下标
        int parent;
        //index: 目前要删除元素x的下标，會變動
        for (parent = index; parent * 2 <= list.size() - 1; parent = index) {
            //左子樹下标
            index = parent * 2;
            //如果存在右子節點，且右子節點大于左子節點，則轉向右子節點
            if (index < list.size() - 1 && list.get(index) < list.get(index + 1)) {
                //右子樹大，指向右子樹
                index++;
            }
            //此時index指向的是孩子節點中較大的數
            //如果父節點比左右子節點都大，則不用交換
            if (tmp > list.get(index)) {
                break;
            } else {
                // 子樹上移，替換目前結點
                list.set(parent, list.get(index));
            }
        }
        //找到合适位置後，在指派
        list.set(parent, list.get(tmp));
        list.remove(list.size() - 1);
    }
           

最小堆中删除元素

public void delete(int x) {
        //判斷堆是否是空堆
        if (list.isEmpty()) {
            return;
        }
        //判斷有無該元素
        if (!list.contains(x)) {
            return;
        }
        //該元素下标
        int index = list.indexOf(x);
        //獲得數組最後一個元素下标，即完全二叉樹中最右子樹的下标
        int tmp = list.size() - 1;
        //将要删除的x和tmp交換位置，即用最後一個元素替換被删除的位置
        list.set(index, list.get(tmp));
        //下濾
        //父節點下标
        int parent;
        for (parent = index; parent * 2 < list.size() - 1; parent = index) {
            //左子節點下标
            index = parent * 2;
            //如果存在右子節點，且右子節點小于左子節點，則轉向右子節點
            if (index != list.size() - 1 && list.get(index) > list.get(index + 1)) {
                index++;
            }
            //此時index是指向孩子節點中較小值的節點
            //如果index指向值小于x，則不用交換
            if (x < list.get(index)) {
                break;
            } else {
                //比左右子樹大，需要交換位置
                list.set(parent, list.get(index));
            }
        }
        //找到合适位置後，在指派
        list.set(parent, list.get(tmp));
        list.remove(list.size() - 1);
    }
           

擷取最值

最大堆和最小堆的最值都在樹的根節點即數組第一位

擷取最大堆的最大值

public int getMax() {
        return list.get(1);
    }
           

擷取最小堆的最小值

public int getMin() {
        return list.get(1);
    }
           

說完堆的實作，下文會談及堆的應用