分解商業周期時間序列：線性濾波器、HP濾波器、Baxter濾波器、Beveridge Nelson分解等去趨勢法|附代碼資料

本文包含各種過濾器，可用于分解南非GDP的方法。我們做的第一件事是清除目前環境中的所有變量。這可以通過以下指令進行（點選文末“閱讀原文”擷取完整代碼資料）。

分解南非GDP資料

本文包含各種過濾器，可用于分解南非GDP的方法。我們做的第一件事是清除目前環境中的所有變量。這可以通過以下指令進行。

1.  rm(list = ls())
2.  graphics.off()

載入資料

如前所述，南非的GDP資料将其作為時間序列存儲在gdp中，我們執行以下指令。

gdp <- ts(dat.tmp, start = c(1960, 2), frequency = 4)      

為了確定這些計算和提取的結果是正确的，我們檢查一下資料的圖表。

plot(gdp)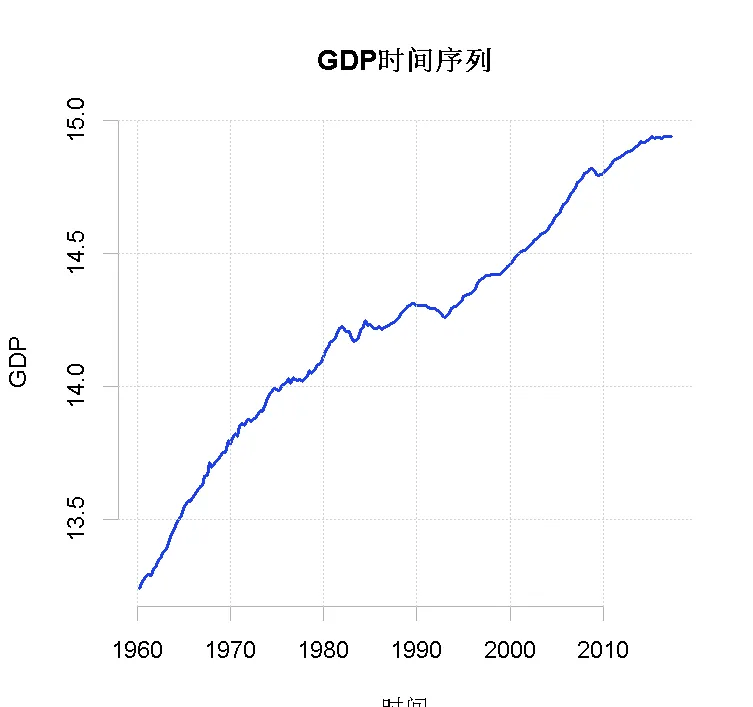      

線性濾波器_去除資料線性趨勢_

為了估計一個線性趨勢，我們可以利用一個包括時間趨勢和常數的線性回歸模型。為了估計這樣一個模型，我們使用lm指令，如下。

1.  lin.mod$fitted.values  # 拟合值與時間趨勢有關
2.  ts(lin.trend, start = c(1960, 1))  # 為趨勢建立一個時間序列變量
3.  gdp - linear  # 周期是資料和線性趨勢之間的差異

回歸的拟合值包含與線性趨勢有關的資訊。這些資訊需要從模型對象lin.mod中提取，在上面的塊中，我們将這些值配置設定給時間序列對象linear。然後從資料中剔除趨勢，就得到了周期。

然後我們可以借助下面的指令來繪制這個結果，其中趨勢和周期被繪制在不同的數字上。

1.  plot.ts(gdp, ylab = "")  
2.  lines(linear, col = "red")  
3.  legend("topleft", legend = c("data", "trend")

霍德裡克 - 普雷斯科特 (Hodrick-Prescott，HP) _濾波器_對資料進行去趨勢處理

要用流行的HP濾波法分解這個資料。在這種情況下，我們将lambda的值設定為1600，這也是對季度資料的建議。

1.  hp(gdp, freq = 1600)
2.  plot.ts(gdp, ylab = "")  # 繪制時間序列
3.  plot.ts(hp.decom$cycle, ylab = "")  # 繪制周期圖

這似乎更準确地反映了我們對南非經濟表現的了解。

點選标題查閱往期内容

​​R語言從經濟時間序列中用HP濾波器，小波濾波和經驗模态分解等提取周期性成分分析​​

轉存失敗重新上傳取消

左右滑動檢視更多

01

02

03

04

用Baxter-King濾波器去趨勢資料

為了利用Baxter-King 濾波器。在這種情況下，我們需要指定周期的頻帶，其上限被設定為32，下限被設定為6。

1.  bk(gdp, pl = 6, pu = 32)
2.  plot.ts(gdp, ylab = "")
3.  plot.ts(cycle, ylab = "")

這似乎再次為南非經濟活動的周期性提供了一個相當準确的表述。還要注意的是，周期的表示比以前提供的要平滑得多，因為噪音不包括在周期中。

Christiano-Fitzgerald濾波器去趨勢資料

這個濾波器的性質與上面提供的非常相似。此外，産生與Baxter-King濾波器高度相似的結果。

1.  plot.ts(gdp, ylab = "")
2.  plot.ts(cfcycle, ylab = "")

用Beveridge-Nelson分解法 "去趨勢 "資料 

為了将資料分解為随機趨勢和平穩周期，我們可以采用Beveridge-Nelson分解法。當采用這種技術時，我們需要指定與平穩部分有關的滞後期的數量。在我下面的例子中，我假設有八個滞後期。

1.  plot.ts(gdp, ylab = "")
2.  lines(bn.trend, col = "red")
3.  plot.ts(bn.cycle, ylab = "")

比較周期的不同衡量标準

然後，我們可以将所有這些結果結合在一張圖上，考慮各自的相似性和差異。在這個例子中，我建立了一個時間序列ts.union，但是我也可以先繪制一個單一的序列，然後再使用lines指令在上面繪制連續的圖。

1.   ts.union(lin.cycle, hp.decom, bp.decom, 
2.      cf.decom, bn.cycle)
3.  plot.ts(comb, ylab = "")

譜分解

在我們考慮使用譜技術之前，最好先清除目前環境中的所有變量，并關閉所有的圖。下一步是確定你可以通過使用library指令來通路這些包中的程式。

1.  library(tsm)
2.  library(TSA)
3.  library(mFilter)

使用譜技術進行分解。我們可以為三個時間序列變量生成數值，然後将它們組合成一個單一的變量。

1.  2 * cos(2 * pi * t * w\[1\]) + 3 * sin(2 * pi * t * 
2.      w\[1\])  # no.obs點上的6個周期的頻率
3.  4 * cos(2 * pi * t * w\[2\]) + 5 * sin(2 * pi * t * 
4.      w\[2\])  #頻率為10個周期的觀察點
5.  6 * cos(2 * pi * t * w\[3\]) + 7 * sin(2 * pi * t * 
6.      w\[3\])  # 在沒有觀測點的情況下，頻率為40個周期
7.  y <- x1 + x2 + x3

為了觀察這些變量，我們可以把它們繪制在一個單獨的軸上。

1.  par(mfrow = c(2, 2), mar = c(2.2, 2.2, 2, 1), cex = 0.8)
2.  plot(x1, type = "l", main = "x1")
3.  plot(x2, type = "l", main = "x2")
4.  plot(x3, type = "l", main = "x3")
5.  plot(y, type = "l", main = "y")

此後，我們可以使用周期圖來考慮這些時間序列變量的每一個屬性。

gram(y, main = "y", col = "red")      

當然，我們可以利用一個過濾器，從總體時間序列變量中去除一些不需要的成分。為此，我們可以應用上下限相對較窄的Christiano-Fitzgerald濾波器。此後，我們使用應用于與周期有關的資訊的周期圖，來調查它是否成功地剔除了一些頻率成分。

1.  cf(y0)
2.  gram(cycle)

這個結果将表明，濾波器已經排除了大部分的高頻率成分。為了看看這個周期與之前的資料有什麼關系，我們把通過濾波器的周期性資訊繪制在分量上。此外，我們還将這個結果繪制在綜合周期的變量上。

1.  plot(x1, type = "l", lty = 1)
2.  lines(cycle, lty = 3, lwd = 3)
3.  plot(y, type = "l", lty = 1)
4.  lines(cycle, lty = 3, lwd = 3)

在這兩種情況下，它似乎都對過程中的趨勢做了合理的描述。

南非商業周期的譜分解法

為了考慮如何在實踐中使用這些頻譜分解，我們現在可以考慮将這些技術應用于南非商業周期的各種特征中。

下一步将是運作所有的過濾器，這些過濾器被應用于識别南非商業周期的不同方法。

現在，讓我們對商業周期的每一個标準應用一個周期圖。

線性濾波器提供了一個很差的結果，因為趨勢明顯占主導地位（這不是周期應該有的）。這與Hodrick-Prescott濾波器的特征形成對比，後者的趨勢資訊已經被去除。Baxter & King和Christiano & Fitzgerald的帶通濾波器也是這種情況。在這兩種情況下，噪聲也已經被去除。最後的結果與Beveridge-Nelson分解有關，我們注意到周期包括大量的趨勢和大量的噪聲。

小波分解

為了提供一個小波分解的例子，我們将把該方法應用于南非通貨膨脹的資料。這将允許使用在這個過程中推導出對趨勢的另一種衡量方法，這可以被認為是代表核心通貨膨脹。請注意，這種技術可以應用于任何階數的單整資料，是以我們不需要首先考慮變量的單整階數。

然後，我們将利用消費者價格指數的月度資料，該資料包含在SARB的季度公告中。資料可以追溯到2002年。為了計算通貨膨脹的同比名額，我們使用diff和lag指令。

diff/cpi\[-1 * (length - 11):length\]      

為了確定所有這些變量的轉換都已正确進行，我們對資料進行繪圖。

plot(inf.yoy)      

由于我們在這種情況下主要對識别平滑的趨勢感興趣，我們将使用貝希斯函數。這樣的函數是Daubechies 4小波，它應用修正的離散小波變換方法。此外，我們還将使用三個母小波來處理各自的高頻成分。

wt(yoy, "d4")      

然後我們可以為每個獨立的頻率成分繪制結果，如下所示。

1.  plot.ts(yoy)
2.  for (i in 1:4) plot.ts(d4\[\[i\]\]

如果我們現在想在資料上繪制趨勢（父小波）。

1.  plot.ts(inf, ylab = "inf")
2.  lines(ren)

請注意，由于各自的頻段是相加的，我們可以将其中一個母頻段加入到趨勢中，如下所示。

1.  inf.tmp <- inf.tren + inf.d4$w3
2.  inf.tren2 <- ts(inf.tmp, start = c(2003, 1), frequency = 12)
3.  plot.ts(inf.yoy, ylab = "inf")
4.  lines(inf.tren2, col = "red")

相關經濟變量的周期性成分之間的相關性

為了确定周期的特征是否合适，我們可以考慮宏觀經濟總量的一些不同周期性方法之間的相關性。例如，我們可以考慮産出和生産（或就業）的周期性在不同的滞後期應該是相關的。如果它們不相關，那麼該方法可能無法準确描述各自變量的周期性成分。

在本文使用的例子中，代碼可能有點難以了解，但我們鼓勵你自己去研究，以提高你對這個編碼環境的總體了解。 

下一步是讀入資料并為資料的各種周期性成分建立一些矩陣。

1.  yd <- dat\[5:n.obs, \] - dat\[1:(n.obs - 4), \]  # 存儲輸出
2.  yc_li <- matrix(rep(0, n.obs * n.var), ncol = n.var)
3.  yc_hp <- matrix(rep(0, n.obs * n.var), ncol = n.var)
4.  yc_bp <- matrix(rep(0, n.obs * n.var), ncol = n.var)
5.  yc_bn <- matrix(rep(0, n.obs * n.var), ncol = n.var)

使用上面包含的方法對資料進行過濾。

1.  for (i in 1:n) {
2.      # 用線性濾波器對資料進行去趨勢處理
3.      lin.mod <- lm(dat\[, i\] ~ time(dat\[, i\]))
4.      # 用HP濾波器去趨勢資料
5.      yc_hp\[, i\] <- hp.cycle
6.      #用帶通濾波器去趨勢資料
7.      yc_bp\[, i\] <- bp.cycle
8.      #  Beveridge-Nelson分解
9.      yc_bn\[, i\] <- bn.\[, 2\]
10.  }

計算不同提前期和滞後期的相關關系。

1.  for (i in 1:n) {
2.      for (j in 1:n.var) {
3.          c\_li <- leadlag(yc\_li\[, i\], yc_li\[, j\], maxLeadLag)
4.          c\_hp <- leadlag(yc\_hp\[, i\], yc_hp\[, j\], maxLeadLag)
5.          c_bp 
6.          c_bn
7.          c_yd 
8.          for (k in 1:5) {
9.              ynamesLong\[(cnt + k), 1\] <- paste(ynames.tmp)
10.          }
11.          cnt <- cnt + 5

繪制結果。

1.  # 線性趨勢
2.  barplot(corrStylizedFact)
3.  box()

1.  # hp濾波器
2.  op <- par(mfrow = c(1, 3))
3.  barplot(corrStyli, ylim = c(-1, 1))
4.  box()

1.  # beveridge nelson 分解
2.  barplot(coracts, ylim = c(-1, 1), col = "red")
3.  box()