機器學習-樸素貝葉斯分類器

一. 機率知識

• 先驗機率：先驗機率（prior probability）是指根據以往經驗和分析得到的機率

• 後驗機率：後驗機率,事情已經發生，要求這件事情發生的原因是由某個因素引起的可能性的大小

  後驗機率就是條件機率

  p(c|x) = p(x|c)p(c)/p(x)  
  
    貝葉斯機率引入先驗知識和邏輯推理來處理不确定的命題
             

• 事情還沒有發生，要求這件事情發生的可能性的大小，是先驗機率。事情已經發生，要求這件事情發生的原因是由某個因素引起的可能性的大小，是後驗機率。
• 先驗機率的計算比較簡單，沒有使用貝葉斯公式；而後驗機率的計算，要使用貝葉斯公式，而且在利用樣本資料計算邏輯機率時，還要使用理論機率分布，需要更多的數理統計知識

二. 貝葉斯分類器基本原理

1. 貝葉斯判定準則

假設訓練集為

T = {(x1,y1),(x2,y2),....,(xN,yN)}

, 有 K 中标記類型，标記集

y = {c1,c1,...,cK}

定義損失函數

L(Y=ck,f(x))

為将樣本 x 分類錯誤所産生的損失

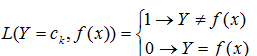
• 基于後驗機率可以得到将樣本 x 分類為 ci 産生的期望損失，即在樣本x上的‘條件風險’

  

  注：期望損失也稱為風險

• 對于分類準則f(x),總體風險為：

  

我們的任務就是找到一個分類準則使總體風險最小化。如果對于每個樣本 x ，若f(x)能最小化條件風險 R(f(x)|x) ,則總體風險 R(f) 也将最小化。

• 貝葉斯判定準則： 為了最小化總體風險，隻需在每個樣本上選擇那個能使條件風險R(c|x)最小的類别标記

  

上式為最小分類錯誤的貝葉斯最優分類器，即對每個樣本x，選擇能使後驗機率 P(c | x)最大的類别标記，是以期望風險最小化準則就是後驗機率最大化準則

2. 樸素貝葉斯

2.1 樸素貝葉斯的原理

經過上面的分析我們得到要想設計最優的貝葉斯判定準則來最小化決策風險，首先要獲得的就是後驗機率 P(c| x)。

由貝葉斯定理可以得到後驗機率的計算公式：

P( c ) 是先驗該機率，P(x | c)是樣本 x 相對于類标記 c 的條件機率，或稱為似然機率

• 先驗機率p©表示樣本空間中各類樣本所占的比例
• 類條件機率p(x | c)是樣本x所有屬性的聯合機率，難以從有限的訓練樣本中直接估計得到，為了避開這個障礙簡化問題，樸素貝葉斯法做了**‘ 屬性條件獨立的 ’**的假設，即對已知類别，假設所有屬性互相獨立。

這就是樸素貝葉斯的由來，樸素貝葉斯分類器中的**’ 樸素 ‘**的含義是： 所有屬性特征互相獨立同等重要。如果屬性之間不互相獨立就是貝葉斯網，一種經典的機率圖模型。

有樸素貝葉斯分類器的的屬性互相獨立的假設條件可以将後驗機率公式變為如下：

由于對于所有類别來說 P(x) 相同，是以可以得到貝葉斯判定準則如下，xi 為樣本 x 第 i 個屬性的值：

這就是樸素貝葉斯分類器的表達式。

是以樸素貝葉斯分類器學習的關鍵是如何求解 P© 和 P(x | c)

2.2 極大似然估計法

初學，目前還沒有搞懂，先占個坑吧！

在樸素貝葉斯算法中，分類器的訓練學習意味着估計 P© 和 P(xi | c) ,可以使用極大似然估計法估計響應的機率，先驗機率和條件機率的極大似然估計如下：

2.3 樸素貝葉斯分類算法

樸素貝葉斯分類器的訓練過程就是基于訓練集來估計類先驗機率 P© , 和每個屬性的條件機率 P(xi | c)

算法執行個體

注：算法和執行個體圖來自于《統計學方法》

2.5 貝葉斯估計

實作算法中可能出現的問題

• 下溢出問題

  訓練樸素貝葉斯分類器之後，當有新樣本時，會計算樣本屬于某個類别的機率

  P(i) = P(ci) P(w0 | ci) P(w1 | ci) ... P(wk | ci)

  在計算機率是由于太多很小的數相乘，程式會下溢出或者得不到正确答案(比如python程式在乘法中得到非常小的輸時會四舍五入)

  一種解決方法是對上面的乘法計算公式取對數将乘法轉化為加法，

  ln(a*b) = ln(a) + ln(b)

  ,通過對數避免下溢出或四舍五入，采用對數進行處理不會有任何損失，不會影響最終結果(因為算法最後是通過比較各個類别機率大小決定樣本的類别，而不是傳回機率本身)

• 訓練集中特征不存在，機率為零

  在計算條件機率時，如果某個屬性在訓練集中沒有和某個類同僚出現，那麼這個條件機率就為0，這樣在最後計算樣本屬于該類的機率時不管其他屬性如何，這個機率都為零，為了避免其他屬性攜帶的資訊被訓練集中未出現的屬性抹去，通常要進行**“平滑”**，常用拉普拉斯平滑。

貝葉斯估計

用極大似然估計會出現所要計算的機率為0的情況，會影響到後驗機率的計算進而影響最終的判定結果，使分類産生偏差。解決這一問題的方法是使用貝葉斯估計代替極大似然估計，下面公式是先驗機率和條件機率的貝葉斯估計：

λ ≧ 0 ，當 λ = 0 時，就是最大似然估計；當 λ = 1 時， 就是拉普拉斯平滑

2.5 樸素貝葉斯分類器的實作方式

• 基于高斯分布模型

  GuassianNB

  :高斯樸素貝葉斯算法是基于假設特征服從高斯分布
• 基于貝努利模型

  MultinomialNB

  :用于實作服從多項式分布資料的樸素貝葉斯算法，常用于文本分類(文本資料經常用詞向量來表示)
• 基于多項式模型

  BernoulliNB

  :用于實作服從多變量貝努利分布資料的樸素貝葉斯算法，這種算法要求樣本表示成二進制特征向量

三. 算法程式設計實作

1. python 實作樸素貝葉斯算法

#程式是基于電子郵件垃圾過濾的執行個體對樸素貝葉斯的實作
import re
import numpy as np

def spamTest():
    docList = []    #存儲文本分割成的字元串清單
    classList = []  #存儲每個郵件的類别
    #一共有50封郵件，25封垃圾郵件，25封正常郵件，将每封郵件轉化成單次向量，添加到docList中，并将郵件類型添加到classList中
    for i in range(1,26):
        #file1 = "E:\courseware\machine leaning\code\MachineLearningInAction\Ch04\email\spam\%d.txt" % i
        stringOfText = open("E:\courseware\machine leaning\code\MachineLearningInAction\Ch04\email\spam\%d.txt" % i, 'r', encoding='gbk', errors='ignore').read()
        wordList = textParse(stringOfText)
        docList.append(wordList)
        classList.append(1)
        #file2 = "E:\courseware\machine leaning\code\MachineLearningInAction\Ch04\email\ham\%d.txt" % i
        stringOfText = open("E:\courseware\machine leaning\code\MachineLearningInAction\Ch04\email\ham\%d.txt" % i, 'r', encoding='gbk', errors='ignore' ).read()
        wordList = textParse(stringOfText)
        docList.append(wordList)
        classList.append(0)
    #利用docList獲得詞彙表向量
    vocabList = createVocabList(docList)
    #分割訓練集和測試集，一共有50個樣本，從中選出10個樣本作為測試集
    trainIndex = list(range(50))
    testIndex = []
    for i in range(10):
        index = int(np.random.uniform(0, len(trainIndex))) #從0到len的均勻分布中随機選取一個整數
        testIndex.append(trainIndex[index])
        trainIndex.pop(index)
    trainSet = []
    trainClass = []
    #将訓練索引中對應的文檔向量添加到訓練集
    for docIndex in trainIndex:
        trainSet.append(setOfWords2Vec(vocabList, docList[docIndex]))
        trainClass.append(classList[docIndex])
    #用訓練集訓練分類器
    p0Vect, p1Vect, p1 = fit(np.array(trainSet), np.array(trainClass))
    #用測試集才評估訓練的分類器
    errorCount = 0
    for docIndex in testIndex:
        wordVector = setOfWords2Vec(vocabList, docList[docIndex])
        if predict(wordVector, p0Vect,p1Vect,p1) != classList[docIndex]:
            errorCount += 1
    errorRate = float(errorCount) / len(testIndex)
    print("The error rate is:%f" % errorRate)

#将整個文本組成的字元串按word分割成字元串清單
def textParse(testString):
    stringListOfText = re.split(r'\W*', testString)
    return [s.lower() for s in stringListOfText if len(s) > 2]

#建立詞彙表向量，裡面包含出現在所有文本中的word
def createVocabList(dataSet):
    vocabList = set([])
    for text in dataSet:
        vocabList = vocabList | set(text)  # | 的作用是集合求并集或者按位求或(or)的操作
    return list(vocabList)

#将一個文本的詞向量轉化成文檔向量，向量每個元素為0或1，表示文本中的單詞是否在詞彙表中出現，eg[0,1,0,1,1,1]
def setOfWords2Vec(vocabList, wordSet):
    resultVec = [0]*len(vocabList)
    for word in wordSet:
        if word in vocabList:
            resultVec[vocabList.index(word)] = 1
    return resultVec

#樸素貝葉斯分類器的訓練函數,以二分類為例
def fit(trainSet,trainClass):
    numDocs = len(trainClass)
    numWords = len(trainSet[0])
    p1 = (sum(trainClass)+1) / (float(numDocs)+2)
    p0Num = np.ones(numWords)
    p1Num = np.ones(numWords)
    p0Denom = 2.0
    p1Denom = 2.0
    for i in range(numDocs):
        if trainClass[i] == 1:
            p1Num += trainSet[i]
            #p0Denom += sum(trainSet[i])
            p0Denom += 1
        else:
            p0Num += trainSet[i]
            #p1Denom +=sum(trainSet[i])
            p1Denom += 1
    p0Vec = np.log(p0Num / p0Denom)
    p1Vec = np.log(p1Num / p1Denom)
    return p0Vec, p1Vec, p1

def predict(testVec, p0Vec, p1Vec, pClass1):
    p1 = sum(testVec * p1Vec) + np.log(pClass1)
    p0 = sum(testVec * p0Vec) + np.log(1.0 - pClass1)
    if p0 > p1:
        return 0
    else:
        return 1

if __name__ == '__main__':
    spamTest()
           

程式内容參考 《機器學習實戰》

2. 樸素貝葉斯在 scikit-learn中的實作

import re
from sklearn import naive_bayes
from sklearn.model_selection import train_test_split

def naive_bayesian():
    #加載資料并劃分訓練集和測試集
    docList = []    #存儲文本分割成的字元串清單
    classList = []  #存儲每個郵件的類别
    #一共有50封郵件，25封垃圾郵件，25封正常郵件，将每封郵件轉化成單次向量，添加到docList中，并将郵件類型添加到classList中
    for i in range(1,26):
        #file1 = "E:\courseware\machine leaning\code\MachineLearningInAction\Ch04\email\spam\%d.txt" % i
        stringOfText = open("E:\courseware\machine leaning\code\MachineLearningInAction\Ch04\email\spam\%d.txt" % i,encoding='gbk', errors='ignore').read()
        wordList = textParse(stringOfText)
        docList.append(wordList)
        classList.append(1)
        #file2 = "E:\courseware\machine leaning\code\MachineLearningInAction\Ch04\email\ham\%d.txt" % i
        stringOfText = open("E:\courseware\machine leaning\code\MachineLearningInAction\Ch04\email\ham\%d.txt" % i, encoding='gbk', errors='ignore' ).read()
        wordList = textParse(stringOfText)
        docList.append(wordList)
        classList.append(0)
    #利用docList獲得詞彙表向量
    vocabList = createVocabList(docList)
    dataList = []
    for docIndex in range(50):
        dataList.append(setOfWords2Vec(vocabList, docList[docIndex]))
    #劃分訓練集和測試集
    x_train, x_test, y_train, y_test = train_test_split(dataList, classList)
    #建立模型
    model = naive_bayes.GaussianNB()
    #訓練模型
    model.fit(x_train, y_train)
    #用測試集測試模型
    accuracy = model.score(x_test,y_test)
    print("精确度為：%f%%" % (accuracy*100))

#将整個文本組成的字元串按word分割成字元串清單
def textParse(testString):
    stringListOfText = re.split(r'\W*', testString)
    return [s.lower() for s in stringListOfText if len(s) > 2]

#建立詞彙表向量，裡面包含出現在所有文本中的word
def createVocabList(dataSet):
    vocabList = set([])
    for text in dataSet:
        vocabList = vocabList | set(text)  # | 的作用是集合求并集或者按位求或(or)的操作
    return list(vocabList)

#将一個文本的詞向量轉化成文檔向量，向量每個元素為0或1，表示文本中的單詞是否在詞彙表中出現，eg[0,1,0,1,1,1]
def setOfWords2Vec(vocabList, wordSet):
    resultVec = [0]*len(vocabList)
    for word in wordSet:
        if word in vocabList:
            resultVec[vocabList.index(word)] = 1
    return resultVec

if __name__ == '__main__':
    naive_bayesian()
           

程式使用的郵件資料在我的 github 上可以下載下傳 樸素貝葉斯-郵件資料集和程式