splay詳解

引入
splay的建構
- 基礎操作
- - 建樹
  - get
  - rotate
  - splay
  - insert
  - kth
  - delete
  - find
  - pre
  - suc
注意事項
splay應用

引入

splay是一種BST，可以維護靜态區間k小

也可以當作區間樹，維護區間資訊（求和，最大子段和，翻轉區間，等等）

時間一般O(nlogn)（均攤），splay操作滿足其穩定性

但是常數巨大，接近100，慎用

splay的建構

一個完整的splay包含以下變量：

fa：此節點的父親
val：此點的權值
cnt：此權值的數量（區間樹中則不需要）
ch[2]：此點的兒子
sz：它以及兒子的大小
tag：lazytag（如果有需要）

接下來是一些操作

基礎操作

建樹

可以一個一個insert，也可以直接構造滿二叉樹

int build(int l,int r,int f){
    if(l>r) return 0;
    int mid=((l+r)>>1),x;
    if(top) x=rb[top--];
    else x=++tot;
    t[x].fa=f;
    t[x].val=a[mid];
    t[x].rev=t[x].laz=0;
    t[x].ls=t[x].rs=Max(a[mid],0);
    t[x].ch[0]=build(l,mid-1,x);
    t[x].ch[1]=build(mid+1,r,x);
    push_up(x);
    return x;
}

get

擷取此點在父親那裡的位置

int get(int x){
    return (t[t[x].fa].ch[1]==x);
}

rotate

splay基礎操作，把兩個點旋轉之後卻不能破壞BST條件

有一個規律：此點的在（父親在祖父那裡的位置）的位置的兒子不會變

void rotate(int x){
    int f=t[x].fa;int g=t[f].fa;
    int kx=get(x),kf=get(f); 
    t[t[x].ch[kx^1]].fa=f;
     t[f].ch[kx]=t[x].ch[kx^1];//不滿足條件的兒子轉到原來此點在父親那裡的地方
    t[f].fa=x;
     t[x].ch[kx^1]=f;//父親變成此點的兒子
    t[x].fa=g;
     t[g].ch[kf]=x;//此點變成祖父的兒子
    push_up(f);
    push_up(x);
}

splay

核心操作，把一個點旋轉到根，確定平衡性，在修改操作之後

一般用雙旋滿足平衡性

對于不同父親和兒子的相對位置，有以下兩種情況：

SPLAY① 入門引入splay的建構注意事項splay應用

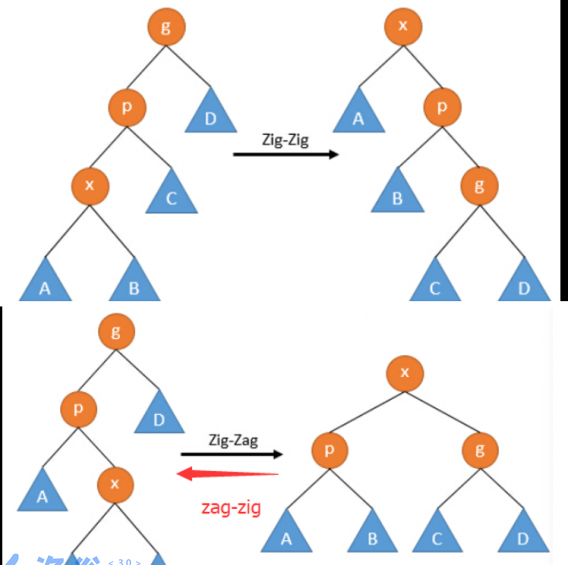
第一種先轉父親，第二種先轉兒子

void splay(int x,int v){
    while(t[x].fa!=v){
        if(t[t[x].fa].fa!=v){ //注意别轉多了
            rotate(get(x)==get(t[x].fa)?t[x].fa:x);// 如果get(x)==get(fa) 就旋轉父親，否則旋轉兒子
        }
        rotate(x);//第二下一定是旋轉x
    }
    if(!v) rt=x;//換根
}

insert

我們要在pos處加入len個數，插入之後還要滿足平衡樹平衡（中序周遊要嚴格單調）的條件，應該怎麼插入呢？

把pos splay到根，再把pos+1 splay到根的右兒子處，那麼pos+1的點的左兒子就一定是pos到pos+1之間的數，也就是空的

那麼在這時把要插入的區間構成一顆滿二叉樹，再把根和pos+1連接配接，就完成了插入

插入完成之後記得push_up

要更新資訊

void insert(int l,int len){
    int r=l+1;
    l=kth(l+1);r=kth(r+1);
    splay(l,0);splay(r,l);//提取區間
    for(int i=1;i<=len;i++){
        a[i]=read();
    }
    t[r].ch[0]=build(1,len,r);
    n+=len;
    push_up(r);push_up(l);//先pushr，因為在下面
}

kth

重點操作，查詢第k大，用splayBST的性質搜尋即可

查詢到一個點時，可分為幾個區間

① k <= 左子樹size，直接遞歸左子樹

② 左子樹size < k <= 左size+cnt[now]，目前值！

⑨ k > 左size+cnt[now] 先減去左size+cnt[now]，再遞歸右子樹

區間k大的話可以先提取區間！

int kth(int k){
    int x=rt;
    while(1){
        push_down(x);
        if(k<=t[t[x].ch[0]].sz){
            x=t[x].ch[0];
        }else if(k==t[t[x].ch[0]].sz+1){
            return x;
        }else{
            k-=t[t[x].ch[0]].sz+1;
            x=t[x].ch[1];
        }
    }
}

delete

删除此點，提取區間後斷開聯系就可以，注意有多個的情況要–cnt，不斷聯系

區間樹：

void recycle(int x){
    if(!x) return;
    rb[++top]=x;
    recycle(t[x].ch[0]);
    recycle(t[x].ch[1]);
} 
void del(int l,int r){
    n-=r-l+1;
    l=kth(l);r=kth(r+2);
    splay(l,0);splay(r,l);
    recycle(t[r].ch[0]);//recycle是記憶體回收
    t[r].ch[0]=0;
    push_up(r);
    push_up(l);
}

權值BST：

inline void del(long long key){
    long long pr=pre(key),su=suc(key);
    splay(pr,0);
    splay(su,pr);
    long long u=ch[su][0];
    //把key的前驅伸展到rt，後繼伸展到rt的右兒子
    //那麼key一定是後繼的左兒子，而且沒有兒子
    if(cnt[u]>1){
        cnt[u]--;
        splay(u,0);
    }else{
        ch[su][0]=0;
        splay(su,0);
        cnt[u]=0;
    } 
}

find

把距這個值最近的值splay到根

inline void find(long long key){
    long long u=rt;
    while(val[u]!=key&&ch[u][key>val[u]]) u=ch[u][key>val[u]];
    splay(u,0);
}

pre

求前驅，先find

然後檢查這個值在它前面還是在後面

在前面一定是前驅

在後面的話，一定是根左子樹中最大的

inline long long pre(long long key){
    find(key);
    if(val[rt]<key) return rt;
    long long u=ch[rt][0];
    while(ch[u][1]){
        u=ch[u][1];
    }
    return u;
}

suc

求後繼，同pre

inline long long suc(long long key){
    find(key);
    if(val[rt]>key) return rt;
    long long u=ch[rt][1];
    while(ch[u][0]){
        u=ch[u][0];
    }
    return u;
}

基礎操作就先這麼多了，之後再更新進階操作

注意事項

要多splay
delete讨論cnt>1?
insert更新資訊，要找是否已有此節點
rotate注意順序和方向，要push_up

splay應用

基礎運用:luogup3369普通平衡樹

#include<iostream>
#include<cstdio>
using namespace std;
long long read(){
    char ch=getchar();long long x=0,pos=1;
    for(;!isdigit(ch);ch=getchar()) if(ch=='-') pos=0;
    for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
    return pos?x:-x;
}
const long long maxn=1000111;
long long n,fa[maxn],val[maxn],cnt[maxn],ch[maxn][3],sz[maxn],rt,tot;
inline long long get(long long u){
    return (ch[fa[u]][1]==u);
}
inline void push_up(long long u){
    sz[u]=sz[ch[u][0]]+sz[ch[u][1]]+cnt[u];
}
inline void rotate(long long u){
    long long f=fa[u];long long g=fa[f];long long k=get(u);
    fa[u]=g;
     ch[g][get(f)]=u;
    fa[ch[u][k^1]]=f;
     ch[f][k]=ch[u][k^1];
    fa[f]=u;
     ch[u][k^1]=f;
     
    push_up(f);
    push_up(u); // ※※※ 
}
inline void splay(long long u,long long v){
    while(fa[u]!=v){
        long long f=fa[u];
        if(fa[f]!=v){
            rotate((get(f)==get(u)?f:u));
        }
        rotate(u);
    }
    if(!v) rt=u;
}
inline void insert(long long key){
    long long u=rt,p=0;
    while(u&&val[u]!=key){
        p=u;
        u=ch[u][key>val[u]];
    }
    if(u) ++cnt[u];
    else{
        u=++tot; 
        val[u]=key;
        if(p){
            ch[p][key>val[p]]=u;
        }
        sz[u]=1;
        fa[u]=p;
        cnt[u]=1;
        ch[u][0]=ch[u][1]=0;
    } 
    splay(u,0);
}
inline void find(long long key){
    long long u=rt;
    while(val[u]!=key&&ch[u][key>val[u]]) u=ch[u][key>val[u]];
    splay(u,0);
}
inline long long rnk(long long key){
    find(key);
    return sz[ch[rt][0]];//有-inf這個點，不用加一 
}
inline long long kth(long long k){
    ++k;// -inf
    long long u=rt;
    while(1926){
        if(sz[ch[u][0]]+cnt[u]<k) k-=(sz[ch[u][0]]+cnt[u]),u=ch[u][1];
        else if(k<=sz[ch[u][0]]) u=ch[u][0];
        else return val[u]; 
    }
    //k < sz[ch[u][0]]: 在左子樹中
    //sz[ch[u][0]] < k <= sz[ch[u][0]]+cnt[u] 為目前值
    //否則是右子樹中 
}
inline long long pre(long long key){
    find(key);
    if(val[rt]<key) return rt;
    long long u=ch[rt][0];
    while(ch[u][1]){
        u=ch[u][1];
    }
    return u;
} 
inline long long suc(long long key){
    find(key);
    if(val[rt]>key) return rt;
    long long u=ch[rt][1];
    while(ch[u][0]){
        u=ch[u][0];
    }
    return u;
}
inline void del(long long key){
    long long pr=pre(key),su=suc(key);
    splay(pr,0);
    splay(su,pr);
    long long u=ch[su][0];
    //把key的前驅伸展到rt，後繼伸展到rt的右兒子
    //那麼key一定是後繼的左兒子，而且沒有兒子
    if(cnt[u]>1){
        cnt[u]--;
        splay(u,0);
    }else{
        ch[su][0]=0;
        splay(su,0);
        cnt[u]=0;
    } 
}
int main(){
    n=read();
    insert(-192608170);
    insert(192608170);
    long long x,opt;
    for(long long i=1;i<=n;i++){
        opt=read();x=read();
        if(opt==1){
        	insert(x);
            continue;
        }
        if(opt==2){
        	del(x);
            continue;
        }
        if(opt==3){
        	printf("%lld\n",rnk(x));
            continue;
        }
        if(opt==4){
        	printf("%lld\n",kth(x));
            continue;
        }
        if(opt==5){
        	printf("%lld\n",val[pre(x)]);
            continue;
        }
        if(opt==6){
        	printf("%lld\n",val[suc(x)]);
            continue;
        }
    }
    return 0;
}

SPLAY① 入門引入splay的建構注意事項splay應用

splay詳解

引入

splay的建構

基礎操作

建樹

get

rotate

splay

insert

kth

delete

find

pre

suc

注意事項

splay應用

繼續閱讀

樹的基本概念(定義、基本術語、性質)

GSL--GNU Scientific Library

D5|哈希表，善用資料結構

如何成為一名.net 工程師?

BMP檔案結構及圖像每行位元組計算方法

D. Ehab the Xorcist(構造+思維)

查找算法之二分查找查找算法之二分查找

JAVA高效程式設計指南

CQ V1.0分詞bates(基于雙數組tire樹)—應該是目前最快的中文分詞算法

【資料結構】醫院選址

[轉]ISUP信令的IAM消息詳細内容

筆試面試題目：滑動視窗(二)

交通/城市相關的公開的資料集上學時整理的Xie et al., 2020收集的

資料結構與算法（27）——排序（二）

GitHub連夜封殺！這份阿裡 10W 字内部 Java 字面試手冊到底有多強？

Linux裝置模型（中）之上層容器