REALM後續：最近鄰搜尋，MIPS，LSH和ALSH

上一篇介紹​​REALM的文章​​有幾個遺憾。一個是今年ICML審稿并沒有結束，是以标題不太好；二是對文中提到的Maximum Inner Product Search沒有作充分的介紹。發出去的标題已經沒法改了，這篇文章介紹一下MIPS和最近鄰搜尋問題，以及兩個相關的算法。

提示：長公式可以左右滑動檢視哦

問題定義

MIPS的定義很簡單，假設你有一堆d維向量，組成集合X，現在輸入了一個同樣次元的查詢向量q (query)，請從X中找出一個p，使得p和q的點積在集合X是最大的。用公式寫出來就是

這個問題和最近鄰問題很像，最近鄰問題隻要把上面的定義改成找一個p使得p和q的距離最小，假設這個距離是歐氏距離，則如果X中的向量模長都一樣，那兩個問題其實是等價的。然而在很多實際場景例如BERT編碼後的句向量、推薦系統裡的各種Embedding等，這個限制是不滿足的。

最近鄰搜尋其實應用非常廣泛，如圖檔檢索、推薦系統、問答等等。以問答比對為例，雖然我們可以用BERT這樣的大型模型獲得很好的準确度，但如果用BERT直接對語料庫中的所有問題進行計算，将耗費大量的時間。是以可以先用關鍵詞檢索或者向量檢索從語料庫裡召回一些候選語料後再做高精度比對。

樸素的算法

對于MIPS問題，一個直覺的蠻力算法就是計算出所有相關的内積，然後将内積排序，找到最大的那個。對于最近鄰問題其實也類似，即使X中向量模長各不相同，也可以提前計算出來，并不會增加排序的時間複雜度。

内積的計算可以轉換成一個矩陣乘法，在CPU和GPU上都有大量的高效實作。當X中有N個向量時，時間複雜度是O(Nd)，當N不大的時候是可以接受的，但是通常在工業界的大規模系統中，X的規模往往很大，樸素算法就顯得力不從心。

Locality-sensitive hashing

對于某些距離度量（例如歐式距離，cosine距離）下的最近鄰問題，可以使用LSH算法來解決。LSH的思路就像下圖示意的那樣，用hash函數把高維空間的點分到幾個桶裡去，進而減少距離的計算量。

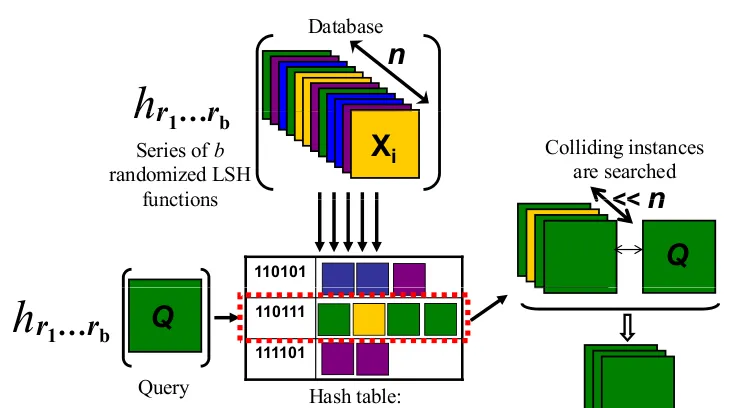
跟普通的哈希函數不同，這個哈希函數是Locality-sensitive的。具體地說就是它有一個神奇的特點：在空間中離得近的點被分到同一個桶的機率大，離得遠的點則大機率被分到不同的桶裡去。或者說對于兩個點x和y，他們被哈希函數分到同一個桶的機率随着距離的增大單調遞減。

這樣在查詢的時候，隻需要精确地比較和查詢向量q處在同一個桶裡的那些x。如果桶足夠多，那便可以将N大大降低，進而提高查詢速度。但需要注意的是，LSH是一個近似算法，有可能産生桶内的向量其實都不是最優解的情況，不同哈希函數發生這種情況的機率都不一樣，也是作為評價哈希函數好壞的重要依據之一，對這部分感興趣的朋友可以讀參考文獻。

下面舉一個具體的例子來解釋一下LSH。假設某個最近鄰問題考慮的距離度量是cosine距離，有一個滿足要求的LSH函數（變換），稱為Random Projection。

如上圖所示，其過程很好了解：

1. 随機取一個空間中的超平面将空間分為兩半，X内位于某一半的點标為0，其他标為1；
2. 重複第一步K次。

完成之後，X中的每個點便得到了一個由K個0，1組成的表示（signature）。例如重複了K=32次，那每個點都被分到了一個用一個int32類型的整數編号的桶裡。如果這些點在空間中分布足夠均勻，那麼我們将可以期望每個桶裡隻有N/2^K個點，當K～logN，則查詢的時間複雜度就約為O(dlogN)。

整個過程建構出了一張哈希表，由于LSH可能會錯過最優解，一個可行的增強魯棒性的做法是用同樣的方法多構造幾張哈希表，借助随機的力量來降低犯錯的機率。參考閱讀[3]是一個講解LSH的視訊，可謂短小精悍，直覺易懂，推薦給大家。

LSH看上去相對于樸素算法确實前進了一大步。但别高興得太早，要達到O(dlogN)的效果必須服從那個很強的假設。而點在空間中分布足夠均勻往往是不太現實的。除此之外，一個LSH隻能适用于某些距離度量，對于MIPS，找不到符合要求的LSH。

Asymmetric LSH(ALSH)

[2]裡證明了找不到可用于MIPS問題的LSH函數，但他們發現對LSH稍作點改動即可将MIPS問題轉變為歐式距離下的最近鄰搜尋問題。改動的關鍵就在于Asymmetric這個詞。在LSH算法中，對查詢向量q和X中的向量做的是同樣（對稱）的變換，而在ALSH中作者對兩者使用了不同（非對稱）的變換。

簡單起見，假設查詢向量q的模長是1。對于X，先做一個放縮變換使得X中所有向量x的所有元素都小于1。然後對X中的向量進行變換P(x)，對查詢向量q做變換Q(x)，P和Q的定義如下：

可以發現，P和Q雖然變換不同，但都會使輸入向量增加m維。進一步觀察可以得到

繼而推導出下面這個關鍵的公式上式右邊的第一項是個常數，第三項由于x的每個值都小于1，是以是随着m的增大以指數的指數的速度趨近于0，是以也就剩下了第二項。第二項包含了我們要求的内積項，而求最大内積就是求最小距離，原問題便轉化成了P(x)和Q(q)間的歐氏距離最近鄰搜尋問題。而P(x)和Q(q)仍然是向量，在歐氏距離下是能夠找到LSH函數快速求出最近鄰問題的近似解的。

上面就是ALSH的主要過程，它的核心技巧是通過“非對稱變換”構造向量進而消除x向量模長對MIPS結果的影響。

前面為了簡單起見引入了一個查詢向量q必須是機關向量的限制，[2]中介紹了怎麼進一步加強這個變換來消除這個限制，在此就不贅述了。

後記

LSH和ALSH的理論證明部分比較複雜，本文可能會有錯誤的地方。由于目前我們的粉絲數太少，還無法在文章留言，有什麼意見和建議大家可以直接到公衆号中給我們發消息。

除了本文介紹的LSH及其變種，在解決向量檢索問題上還有很多有趣的算法和厲害的算法包，我們會在後續的文章中繼續介紹。在今年一月份的時候Google發了一篇叫《Reformer: The Efficient Transformer》的文章，就用到了LSH的算法，近期我們可能也會乘熱打鐵介紹一下這篇文章。

參考閱讀

1. 國内向量檢索引擎Milvus

   ​​​https://milvus.io/cn/docs/about_milvus/index_method.md​​

2. ALSH論文

   ​​​https://papers.nips.cc/paper/5329-asymmetric-lsh-alsh-for-sublinear-time-maximum-inner-product-search-mips.pdf​​

3. LSH講解視訊（牆外）

   ​​​https://www.youtube.com/watch?v=Arni-zkqMBA&list=PLZKSpah6NB5LbjWM9JoOSbZZffwCUwJdh&index=8​​

4. LSH ppt（Stanford）

   ​​​https://graphics.stanford.edu/courses/cs468-06-fall/Slides/aneesh-michael.pdf​​

5. Reformer: The Efficient Transformer

   ​​​https://arxiv.org/pdf/2001.04451.pdf​​