“ 本文的内容包括圖卷積的基礎知識以及相關輔助了解的知識點,相信同學們看完後一定能平滑上手了解GCN!”
作者:苘郁蓁
編輯:happyGirl
具體來說,本文包括什麼:
- 圖網絡的有哪些種類,它們之間的差別和聯系是什麼?
- 圖卷積的地位,圖卷積怎麼了解?
- 有沒有一個圖卷積的通式,各種不同的公式怎麼統一?
- 有沒有一個最簡單的例子說明網絡的訓練過程?
- 想快速上手有哪些代碼實作和庫?
本文不包括
- 傅立葉算子到拉普拉斯算子到拉普拉斯矩陣的數學推倒,感興趣可以看參考文獻。
一文讀懂系列文章:
《一文讀懂Transformer和Attention》(https://zhuanlan.zhihu.com/p/90033981) 《一文讀懂殘差網絡ResNet》(https://zhuanlan.zhihu.com/p/91385516)
圖神經網絡GNN相關系列文章:
《什麼是Weisfeiler-Lehman(WL)算法和WL Test?》 (https://zhuanlan.zhihu.com/p/90645716)
《圖神經網絡庫PyTorch geometric(PYG)零基礎上手教程》 (https://zhuanlan.zhihu.com/p/91229616)
圖網絡的分類
在最開始,我們先梳理一下經常被提到的幾個術語的差別和聯系,也就是Graph Embedding,Graph Neural Network和Graph Convolutional Network的差別和聯系是什麼。
Graph Embedding
圖嵌入(Graph Embedding/Network Embedding,GE),屬于表示學習的範疇,也可以叫做網絡嵌入,圖表示學習,網絡表示學習等等。通常有兩個層次的含義:
- 将圖中的節點表示成低維、實值、稠密的向量形式 ,使得得到的向量形式可以在向量空間中具有表示以及推理的能力,這樣的向量可以用于下遊的具體任務中。例如使用者社交網絡得到節點表示就是每個使用者的表示向量,再用于節點分類等;
- 将整個圖表示成低維、實值、稠密的向量形式 ,用來對整個圖結構進行分類;
圖嵌入的方式主要有三種:
- 矩陣分解: 基于矩陣分解的方法是将節點間的關系用矩陣的形式加以表達,然後分解該矩陣以得到嵌入向量。通常用于表示節點關系的矩陣包括鄰接矩陣,拉普拉斯矩陣,節點轉移機率矩陣,節點屬性矩陣等。根據矩陣性質的不同适用于不同的分解政策。
- DeepWalk: DeepWalk 是基于 word2vec 詞向量提出來的。word2vec 在訓練詞向量時,将語料作為輸入資料,而圖嵌入輸入的是整張圖,兩者看似沒有任何關聯。但是 DeepWalk 的作者發現,預料中詞語出現的次數與在圖上随機遊走節點被通路到底的次數都服從幂律分布。是以 DeepWalk 把節點當做單詞,把随機遊走得到的節點序列當做句子,然後将其直接作為 word2vec 的輸入可以節點的嵌入表示,同時利用節點的嵌入表示作為下遊任務的初始化參數可以很好的優化下遊任務的效果,也催生了很多相關的工作;
- Graph Neural Network: 圖結合deep learning方法搭建的網絡統稱為圖神經網絡GNN,也就是下一小節的主要内容,是以圖神經網絡GNN可以應用于圖嵌入來得到圖或圖節點的向量表示;
Graph Neural Network
圖神經網絡(Graph Neural Network, GNN)是指神經網絡在圖上應用的模型的統稱,根據采用的技術不同和分類方法的不同,又可以分為下圖中的不同種類,例如從傳播的方式來看,圖神經網絡可以分為圖卷積神經網絡(GCN),圖注意力網絡(GAT,縮寫為了跟GAN區分),Graph LSTM等等,本質上還是把文本圖像的那一套網絡結構技巧借鑒過來做了新的嘗試。但在這篇文章中并不會細細介紹下面的每一種,作為入門篇,我們着重了解最經典和最有意義的基礎模型GCN,這也是了解其他模型的基礎。
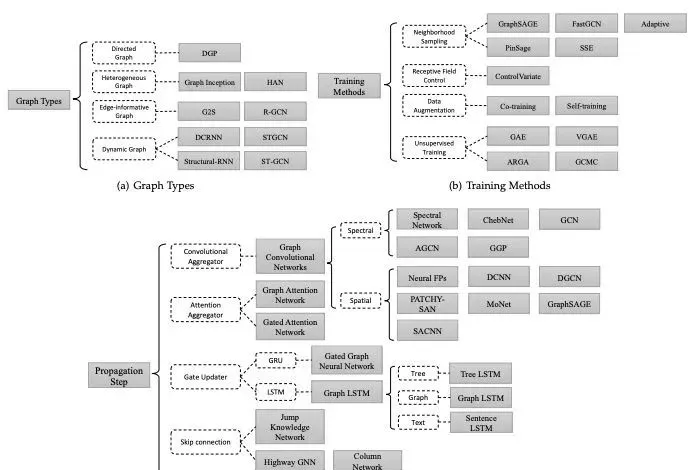
圖神經網絡GNN的分類:分别從圖的類型,訓練的方式,傳播的方式三個方面來對現有的圖模型工作進行劃分
Graph Convolutional Network
圖卷積神經網絡(Graph Convolutional Network, GCN)正如上面被分類的一樣,是一類采用圖卷積的神經網絡,發展到現在已經有基于最簡單的圖卷積改進的無數版本,在圖網絡領域的地位正如同卷積操作在圖像處理裡的地位。
GCN的差別和聯系
如圖2所示,這三個比較繞的概念可以用一句話來概括:圖卷積神經網絡GCN屬于圖神經網絡GNN的一類,是采用卷積操作的圖神經網絡,可以應用于圖嵌入GE。
卷積VS圖卷積
要了解圖卷積網絡的核心操作圖卷積,可以類比卷積在CNN的地位。
如下圖所示,數字圖像是一個二維的離散信号,對數字圖像做卷積操作其實就是利用卷積核(卷積模闆)在圖像上滑動,将圖像點上的像素灰階值與對應的卷積核上的數值相乘,然後将所有相乘後的值相加作為卷積核中間像素對應的圖像上像素的灰階值,并最終滑動完所有圖像的過程。
用随機的共享的卷積核得到像素點的權重和進而提取到某種特定的特征,然後用反向傳播來優化卷積核參數就可以自動的提取特征,是CNN特征提取的基石 。
圖像卷積
然而,現實中 更多重要的資料集都是用圖的形式存儲的,例如社交網絡資訊,知識圖譜,蛋白質網絡,網際網路等等。這些圖網絡的形式并不像圖像,是排列整齊的矩陣形式,而是非結構化的資訊,那有沒有類似圖像領域的卷積一樣,有一個通用的範式來進行圖特征的抽取呢 ?這就是圖卷積在圖卷積網絡中的意義。
對于大多數圖模型,有一種類似通式的存在,這些模型統稱GCNs。是以可以說,圖卷積是處理非結構化資料的大利器,随着這方面研究的逐漸深入,人類對知識領域的處理必将不再局限于結構化資料( CV,NLP),會有更多的目光轉向這一存在範圍更加廣泛,涵蓋意義更為豐富的知識領域。
接下來我們就來逐漸拆解這個範式。
圖卷積
圖結構執行個體
圖的定義
對于圖,我們有以下特征定義:
對于圖
,
為節點的集合,
為邊的集合,對于每個節點
, 均有其特征
,可以用矩陣
表示。其中
表示節點數,
圖卷積的形象化了解
在一頭紮進圖卷積公式之前,我們先從其他的角度了解一下這個操作的實體含義,有一個形象化的了解,我們在試圖得到節點表示的時候,容易想到的最友善有效的手段就是利用它周圍的節點,也就是它的鄰居節點或者鄰居的鄰居等等,這種思想可以歸結為一句話:
圖中的每個結點無時無刻不因為鄰居和更遠的點的影響而在改變着自己的狀态直到最終的平衡,關系越親近的鄰居影響越大。
實際上從鄰居節點擷取資訊的思想在很多領域都有應用,例如word2vec,例如pagerank。關于這個點展開的内容文章[2]有非常詳細的解釋。
更加細節的如何從傅立葉變換到拉普拉斯算子到拉普拉斯矩陣的數學推倒可以轉向部落格[7],為了避免數學功底沒有那麼強的初學者(比如我)被繞暈,我們先建立大綱,不要太發散。
圖相關矩陣的定義
那麼有什麼東西來度量節點的鄰居節點這個關系呢,學過圖論的就會自然而然的想到鄰接矩陣和拉普拉斯矩陣。舉個簡單的例子,對于下圖中的左圖(為了簡單起見,舉了無向圖且邊沒有權重的例子)而言,它的度矩陣
,鄰接矩陣
和拉普拉斯矩陣
分别如下圖所示,度矩陣
隻有對角線上有值,為對應節點的度,其餘為0;鄰接矩陣
隻有在有邊連接配接的兩個節點之間為1,其餘地方為0;拉普拉斯矩陣
為
一個圖的度矩陣,鄰接矩陣和拉普拉斯矩陣
圖卷積的通式
任何一個圖卷積層都可以寫成這樣一個非線性函數:
為第一層的輸入,
,
為圖的節點個數,
為每個節點特征向量的次元,
為鄰接矩陣,不同模型的差異點在于函數
下面介紹幾種具體的實作,但是每一種實作的參數大家都統稱拉普拉斯矩陣。
實作一
其中
為第
層的權重參數矩陣,
這種思路是基于節點特征與其所有鄰居節點有關的思想。鄰接矩陣
與特征
但這樣存在兩個問題:
- 沒有考慮節點自身對自己的影響;
-
鄰接矩陣
沒有被規範化,這在提取圖特征時可能存在問題,比如鄰居節點多的節點傾向于有更大的影響力。
是以實作二和實作三針對這兩點進行了優化。
實作二
拉普拉斯矩陣
- 引入了度矩陣,進而解決了沒有考慮自身節點資訊自傳遞的問題
實作三
對于這裡的拉普拉斯矩陣 ,學名Symmetric normalized Laplacian,也有論文或者部落格寫
- 引入自身度矩陣,解決自傳遞問題;
-
對鄰接矩陣的歸一化操作,通過對鄰接矩陣兩邊乘以節點的度開方然後取逆得到。 具體到每一個節點對
,
其中
分别為節點
的度,也就是度矩陣在節點
可能有一點比較疑惑的是怎麼兩邊乘以一個矩陣的逆就歸一化了? 這裡需要複習到矩陣取逆的本質是做什麼。
我們回顧下矩陣的逆的定義,對于式子
,假如我們希望求矩陣X,那麼當然是令等式兩邊都乘以
,然後式子就變成了
舉個例子對于,單個節點運算來說,做歸一化就是除以它節點的度,這樣每一條鄰接邊資訊傳遞的值就被規範化了,不會因為某一個節點有10條邊而另一個隻有1條邊導緻前者的影響力比後者大,因為做完歸一化後者的權重隻有0.1了,從單個節點上升到二維矩陣的運算,就是對矩陣求逆了,乘以矩陣的逆的本質,就是做矩陣除法完成歸一化。但左右分别乘以節點i,j度的開方,就是考慮一條邊的兩邊的點的度。
常見的拉普拉斯矩陣除了以上舉的兩種,還有
另一種表述
上面是以矩陣的形式計算,可能會看起來非常讓人疑惑,下面從單個節點的角度來重新看下這些個公式(本質是一樣的,上文解釋過,對于單個節點就是除法,對于矩陣就是乘以度矩陣的逆),對于第
層的節點的特征
,對于它的鄰接節點
,
是節點
其中,
,
,
為
的鄰居節點,
為
碼字不易,覺得有收獲記得點贊哦~
更多内容,歡迎點選文末閱讀原文關注作者的專欄和作者交流!
參考文獻
[1] https:// zhuanlan.zhihu.com/p/77729049 圖嵌入的分類
[2] https://www.zhihu.com/question/54504471/answer/630639025 關于圖卷積的實體學解釋
[3] https://www.zhihu.com/question/54504471/answer/332657604拉普拉斯公式推倒細節,包括譜分解和傅立葉變換
[4] http://tkipf.github.io/graph-convolutional-networks 兩篇論文細講
[5] https://github.com/conferencesub/ICLR_2020各種圖卷積核比較
[6] https://persagen.com/files/misc/scarselli2009graph.pdfGNN首次被提出的paper
[7] https://zhuanlan.zhihu.com/p/85287578 拉普拉斯矩陣和拉普拉斯算子的關系
備注:公衆号菜單包含了整理了一本AI小抄,非常适合在通勤路上用學習。