一、 MCMC抽樣
也許讀者會覺得詫異,為什麼在一本介紹主題模型的書中卻看到了抽樣的知識?作者是不是偏題了?
答案當然是沒有。
相信你應該聽說過有一門課程叫做統計學,在這門課程中,抽樣占據着舉足輕重的地位。當統計學的研究者們想要了解一個總體的某些參數時,他們的方案是,先去抽樣獲得樣本,通過樣本參數去估計總體參數。比如,想知道某财經高校學生們(總體)的平均月消費水準(總體參數),做法是:a.先抽樣一部分樣本,如從每個學院抽取20個人去調查他們的月消費水準,假設有20個學院,那麼就獲得了400個人(樣本)的月消費水準;b.算出這400個樣本的平均月消費水準(樣本參數);c.可以認為該财經高校學生們的平均月消費水準估計為這400個樣本的平均月消費水準。
本篇的MCMC抽樣與LDA主題模型的關系類比統計學裡的抽樣。在LDA主題模型的參數求解中,我們會使用MCMC抽樣去做。
MCMC四個字母的含義
第一個MC ,是Monte Carlo(蒙特卡洛)的首字母縮寫。本篇的蒙特卡洛指一種随機模拟方法,以機率和統計理論方法為基礎的一種計算方法,是使用随機數(或更常見的僞随機數)來解決很多計算問題的方法。采樣過程通常通過計算機來來實作。
蒙特卡洛此名由烏拉姆提出,事實上蒙特卡洛是摩納哥公國的一座城市,是著名的賭場,世人稱之為“賭博之國”。衆人皆知,賭博總是和統計密切關聯的,是以這個命名風趣而貼切、不僅有意思而且有意義。
第二個MC:Markov Chain(馬爾科夫鍊)。這是MCMC抽樣中很重要的一個思想,将會在後篇細講。
(一)逆變換采樣
剛剛有提到,蒙特卡洛指一種随機模拟方法,通常通過計算機來實作。然而,從本質上來說,計算機隻能實作對均勻分布的采樣。在此基礎上對更為複雜的分布進行采樣,應該怎麼做呢?這就需要用到逆變換采樣:
溫故兩個定義
對于随機變量 X,如下定義的函數 F:
F(x)=PX≤x,−∞<x<∞ F ( x ) = P X ≤ x , − ∞ < x < ∞
稱為X 的 累積分布函數。對于連續型随機變量 X 的累積分布函數 F(x),如果存在一個定義在實數軸上的非負函數 f(x),使得對于任意實數 x,有下式成立:
F(x)=∫f(t)dt F ( x ) = ∫ f ( t ) d t
則稱 f(x) 為 X 的 機率密度函數。顯然,當機率密度函數存在的時候,累積分布函數是機率密度函數的積分。機率等于區間乘機率密度。
步驟
欲對密度函數 f(x) f ( x ) 采樣,并得到m 個觀察值,則重複下面的步驟 m 次:
1、從Uniform(0,1)中随機生成一個值,用 u 表示。
2、計算反函數 F(−1)(u) F ( − 1 ) ( u ) 的值 x,則x 就是從 f(x) f ( x ) 中得出的一個采樣點。
舉例:
想對一個複雜機率密度函數 f(x) f ( x ) 抽樣,其機率密度形式如下:
F(x)=⎧⎩⎨⎪⎪8x,if0≤x<0.2583−83x,if0.25≤x<1 0,otherwise F ( x ) = { 8 x , i f 0 ≤ x < 0.25 8 3 − 8 3 x , i f 0.25 ≤ x < 1 0 , o t h e r w i s e
1、求 f(x) f ( x ) 的累計分布函數 F(x) F ( x ) :
F(x)=⎧⎩⎨⎪⎪⎪⎪⎪⎪0,ifx<04x2,if0≤x<0.2583x−43x2−13,if0.25≤x<1 1,ifx>1 F ( x ) = { 0 , i f x < 0 4 x 2 , i f 0 ≤ x < 0.25 8 3 x − 4 3 x 2 − 1 3 , i f 0.25 ≤ x < 1 1 , i f x > 1
2、求 F(x) F ( x ) 的反函數: F(−1)(u) F ( − 1 ) ( u )
F(x)=⎧⎩⎨u√2,if0≤u<0.251−3(1−u)√2,if0.25≤x<1 F ( x ) = { u 2 , i f 0 ≤ u < 0.25 1 − 3 ( 1 − u ) 2 , i f 0.25 ≤ x < 1
重複m次逆變換采樣以下步驟:從Uniform(0,1)中随機生成一個值,用 u 表示。計算反函數 F(−1)(u) F ( − 1 ) ( u ) 的值 x,則x 就是從 f(x) f ( x ) 中得出的一個采樣點。最終将采樣點圖像(藍色)與實際密度函數(紅色)比較,得圖如下:
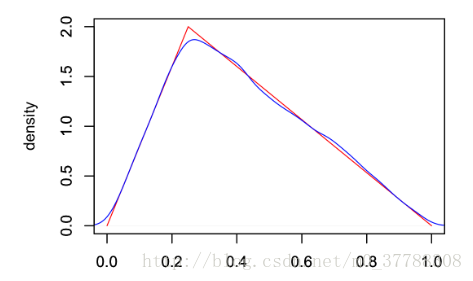 可以看到兩條線幾乎重合,這表明逆變換采樣可以很好的模拟出某些複雜分布。 **存在問題:** 逆變換采樣有求解累積分布函數和反函數這兩個過程,而有些分布的機率分布函數可能很難通過對機率密度p(x)的積分得到,再或者機率分布函數的反函數也很不容易求。這個時候應該怎麼辦呢?此時提出了拒絕采樣的解決方案。
(二)拒絕采樣
欲對逆變換采樣不再适用的密度函數 p(x) p ( x ) 采樣,如果能找到另外一個機率密度為 q(x) q ( x ) 的函數,它相對容易采樣。如采用逆變換采樣方法可以很容易對 q(x) q ( x ) 進行采樣,甚至 q(x) q ( x ) 就是計算機可以直接模拟的均勻分布。此時我們可直接對 q(x) q ( x ) 采樣,然後按照一定的方法拒絕某些樣本,達到接近 p(x) p ( x ) 分布的目的。
步驟
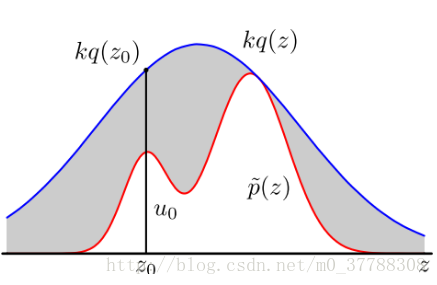 當我們将 q(x) q ( x ) 與一個常數 K 相乘之後,可以實作下圖所示之關系,即 K⋅q(x)将p(x)完全“罩住”:p(x) ≤Kq(x)。重複以下步驟抽樣: •x 軸方向:從q(x)分布抽樣得到 Z0 Z 0 。 •y 軸方向:從均勻分布 (0,Kq(Z0)) ( 0 , K q ( Z 0 ) ) 中抽樣得到 u0 u 0 。 •如果剛好落到灰色區域,否則接受這次抽樣: u0 u 0 > p(Z0) p ( Z 0 ) , 拒絕該樣本。 •重複以上過程。 舉例:利用拒絕采樣計算 π π 值 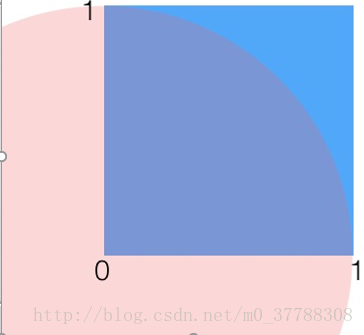 如圖所示,陰影區域有一個邊長為1的正方形,正方形裡有一個半徑為1的1/4圓。則有:S(1/4圓)= 1/4*π*R^2= 1/4π;S(正方形)=1。現在對這個正方形随機取點,某點到原點的距離小于1,則說明它在1/4圓内。可以認為,落在圓内的次數/取點總次數=1/4圓的面積/正方形的面積。即: π=4∗s(正方形)∗落在圓内的次數取點總次數 π = 4 ∗ s ( 正 方 形 ) ∗ 落 在 圓 内 的 次 數 取 點 總 次 數 随着采樣點的增多,最後的結果π會越精準。 這裡也就是用到了拒絕采樣的思想。要計算 π π 值,即尋求對圓這個複雜分布抽樣,圓不好搞定,于是我們選擇了一個相對容易的正方形分布,在對正方形随機取點的時候,如果某點到原點的距離小于1,則說明它在1/4圓内,接受這個樣本,否則拒絕它。 而抽樣的時候; 基于以上思想我們可以利用計算機模組化。
(三)馬爾科夫鍊
馬爾科夫鍊就是第二個MC:Markov Chain。定義為:根據機率分布,可以從一個狀态轉移到另一個狀态,但是狀态轉移之間服從馬氏性的一種分布。
解釋一下定義中提到的兩個名詞:
馬氏性:狀态轉移的機率隻依賴與他的前一狀态。數學表達為: P(Xn+1=k|Xn=kn,Xn−1=kn−1,…,X1=k1)=P(Xn+1=k|Xn=kn) P ( X n + 1 = k | X n = k n , X n − 1 = k n − 1 , … , X 1 = k 1 ) = P ( X n + 1 = k | X n = k n )
狀态轉移:狀态的改變叫做轉移(狀态可以向自身轉移),與不同的狀态改變相關的機率叫做轉移機率。 q(i,j)=q(j|i)=q(i→j): q ( i , j ) = q ( j | i ) = q ( i → j ) : 表示狀态 i轉移到狀态j的機率。
如在天氣事件中,由前天的下雨轉移到昨天的多雲,昨天的多雲轉變到今天的豔陽天。這裡所說的下雨、多雲、豔陽天都是一種狀态。從下雨轉移到多雲,稱之為狀态轉移。而今天的豔陽天隻與昨天的多雲有關,與前天的天氣沒有半點關系,這就是所謂馬氏性。
案例
社會學家經常把人按其經濟狀況分成三類:下、中、上層;我們用1,2,3分别代表這三個階層(對應于馬氏鍊中環境下的三個狀态)。如果一個人的收入屬于下層類别,則他的孩屬于下層收入的機率是0.665,屬于中層的機率是0.28,屬于上層的機率是0.07。這裡彙總了階層收入變化的轉移機率如下圖所示:
 狀态轉移的機率隻依賴與他的前一狀态,也就是考察父代為第i層則子代為第j層的機率。 由此得出轉移機率矩陣: ⎡⎣⎢0.650.150.120.280.670.360.070.180.52⎤⎦⎥ [ 0.65 0.28 0.07 0.15 0.67 0.18 0.12 0.36 0.52 ]
給定目前這一代人處于下、中、上層的機率分布向量是: π0=(π0(1),π0(2),π0(3)) π 0 = ( π 0 ( 1 ) , π 0 ( 2 ) , π 0 ( 3 ) ) ,那麼他們的子女的分布比例将是 π1=π0P π 1 = π 0 P ,孫子代的分布比例将是 π2=π1P=π0P2 π 2 = π 1 P = π 0 P 2 ,以此類推,第n代的分布比例将是 πn=π0Pn π n = π 0 P n . 顯然,第n+1代中處于第j個階層的機率為:
π(Xn+1=j)=∑i=0nπ(Xn=i).P(Xn+1=j|Xn=i) π ( X n + 1 = j ) = ∑ i = 0 n π ( X n = i ) . P ( X n + 1 = j | X n = i )
給定初始機率 π0=(0.21,0.68,0.11) π 0 = ( 0.21 , 0.68 , 0.11 ) ,即第0代的時候各階層占比是(0.21,0.68,0.11)。顯然由此公式我們可以分别計算第一代的第1、2、3階層的占比,第二代的第1、2、3階層的占比,….。
如:計算第一代的第1階層的占比為: 0.21∗.65+0.68∗0.15+0.11∗0.12=0.2517≈0.252 0.21 ∗ .65 + 0.68 ∗ 0.15 + 0.11 ∗ 0.12 = 0.2517 ≈ 0.252
以此類推,各代各階層的占比如下:
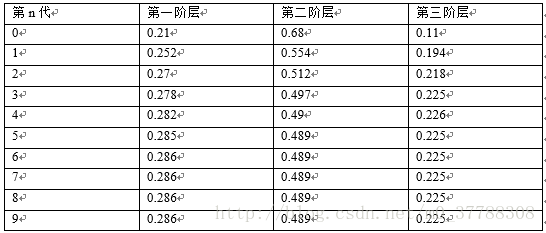 可以看到,從第5代開始,各階層的分布就穩定不變了。這個是偶然的嗎?如若不是,那是初始機率決定的還是轉移機率矩陣決定的呢?接下來驗證一下。 換一個初始機率 π0=(0.75,0.15,0.1) π 0 = ( 0.75 , 0.15 , 0.1 ) ,疊代結果如下: 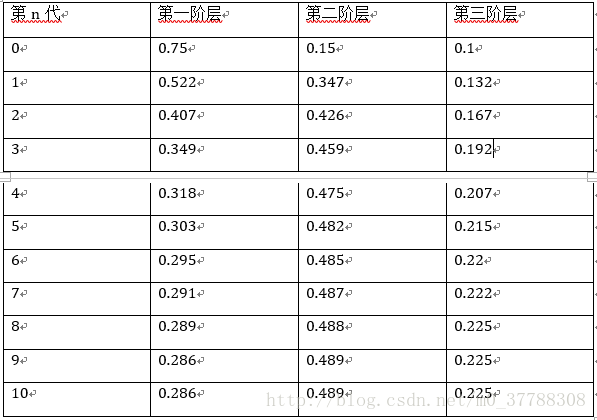 我們發現,到第9代的時候,分布又收斂了,而且收斂的分布都是 π=(0.286,0.489,0.225) π = ( 0.286 , 0.489 , 0.225 ) ,也就是說收斂的分布與初始機率無關。 這裡還有一個神奇的地方:我們計算一下轉移矩陣P的n次幂,發現:
P20=P21=⋯=P100=Pn=⎡⎣⎢0.2860.2860.2860.4890.4890.4890.2250.2250.225⎤⎦⎥ P 2 0 = P 2 1 = ⋯ = P 1 00 = P n = [ 0.286 0.489 0.225 0.286 0.489 0.225 0.286 0.489 0.225 ]
也就是說,當n足夠大的時候, Pn P n 矩陣每一行都收斂到 π=(0.286,0.489,0.225) π = ( 0.286 , 0.489 , 0.225 ) 這個機率分布。于是關于馬氏鍊我們有定理如下:
定理一:(馬氏鍊的平穩分布)
如果一個非周期馬氏鍊具有機率轉移矩陣 P,且它的任何兩個狀态都是連通的,則
limn→∞Pnij lim n → ∞ P i j n
存在且與 i 無關(也即矩陣 P^n 的每一行元素都相同),記 limn→∞Pnij=π(j) lim n → ∞ P i j n = π ( j )
,我們有:
(1) limn→∞Pn=⎡⎣⎢π(1)...π(1).........π(n)...π(n)⎤⎦⎥ lim n → ∞ P n = [ π ( 1 ) . . . π ( n ) . . . . . . . . . π ( 1 ) . . . π ( n ) ]
(2) π(j)=∑∞0π(i)Pij也即π=πP。 π ( j ) = ∑ 0 ∞ π ( i ) P i j 也 即 π = π P 。
(3)π 是方程 π=πP 的唯一非負解。
其中, π=[π(1),π(2),⋯,π(j),⋯],∑∞0π(i)=1 π = [ π ( 1 ) , π ( 2 ) , ⋯ , π ( j ) , ⋯ ] , ∑ 0 ∞ π ( i ) = 1 (符合機率上對分布的要求),π 稱為馬氏鍊的平穩分布。
定理二(細緻平穩條件)
如果非周期馬氏鍊的轉移矩陣 P和分布π(x)滿足:π(i)Pij=π(j)Pji,則π(x)是馬氏鍊的平穩分布,上式被稱為細緻平穩條件。 P 和 分 布 π ( x ) 滿 足 : π ( i ) P i j = π ( j ) P j i , 則 π ( x ) 是 馬 氏 鍊 的 平 穩 分 布 , 上 式 被 稱 為 細 緻 平 穩 條 件 。
以上兩個定理極其重要,是MCMC理論不可缺少的理論基礎。
(四)從馬爾科夫鍊到抽樣
對于給定的機率分布 π(x) π ( x ) ,我們希望有快捷的方式生成它對應的樣本。由于馬氏鍊能收斂到平穩分布,于是一個很漂亮的想法是:如果我們能夠構造一個轉移矩陣為 P的馬氏鍊,使得該馬氏鍊的平穩分布恰好是 π(x) π ( x ) ,那麼我們從任何一個初始狀态出發沿着馬氏鍊轉移,得到一個轉移序列 x1,x2,…,xn,x(n+1),…, x 1 , x 2 , … , x n , x ( n + 1 ) , … , 如果馬氏鍊在第 n 步已經收斂了,于是 x1,x2,…,xn,x(n+1),… x 1 , x 2 , … , x n , x ( n + 1 ) , … 自然是分布 π(x) π ( x ) 的樣本。
馬氏鍊的收斂性質主要有轉移矩陣 P決定,是以基于馬氏鍊做采樣(比如MCMC)
的關鍵問題是如何構造轉移矩陣,使得其對應的平穩分布恰是我們需要的分布 π(x) π ( x ) 。
MCMC采樣
根據細緻平穩理論,隻要我們找到了可以使機率分布 π(x) π ( x ) 滿足細緻平穩分布的矩陣P即可。這給了我們尋找從平穩分布π, 找到對應的馬爾科夫鍊狀态轉移矩P的新思路。
假設我們已經有一個轉移矩陣為Q的馬氏鍊。 q(i,j) q ( i , j ) 表示狀态 i轉移到狀态j的機率.通常情況下,細緻平穩條件不成立,即:
p(i)q(i,j)≠p(j)q(j,i) p ( i ) q ( i , j ) ≠ p ( j ) q ( j , i )
對上式改造使細緻平穩條件成立:引入一個α(i,j)和α(j,i) ,并讓等式兩端取等:
p(i)q(i,j)α(i,j)=p(j)q(j,i)α(j,i) p ( i ) q ( i , j ) α ( i , j ) = p ( j ) q ( j , i ) α ( j , i )
問題是什麼樣的α(i,j)和α(j,i)可以使等式成立呢?按照對稱性,可以取:
α(i,j)=p(j)q(j,i) α ( i , j ) = p ( j ) q ( j , i )
α(j,i)=p(i)q(i,j) α ( j , i ) = p ( i ) q ( i , j )
是以我們改造後的馬氏鍊 Q′ Q ′ 如下。并且 Q′ Q ′ 恰好滿足細緻平穩條件,是以馬氏鍊 Q′ Q ′ 的平穩分布就是 P(x) P ( x ) 。
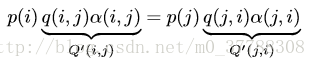 **步驟** (1)初始化馬氏鍊初始狀态 X0=x0 X 0 = x 0 (2)對 t=0,1,2,3,… t = 0 , 1 , 2 , 3 , … 循環一下過程進行采樣: 第 t t 時刻馬氏鍊狀态為Xt=xtXt=xt,采樣 y∼q(x|x(t)) y ∼ q ( x | x ( t ) ) ; 從均勻分布采樣 u∼Uniform[0,1]; u ∼ U n i f o r m [ 0 , 1 ] ; 如果 u<α(xt,y)=p(y)q(xt│y), u < α ( x t , y ) = p ( y ) q ( x t │ y ) , 則接受 xt→y, x t → y , 即 xt+1)→y x t + 1 ) → y ;否則不接受機率轉移,即 Xt+1=xt。 X t + 1 = x t 。
(五)Metropolis-Hastings采樣
以上過程不論是離散或是連續分布,都适用。
以上的MCMC采樣算法已經能正常采樣了,但是馬氏鍊Q在轉移的過程中的接受率α(i,j)可能偏小,這樣我們會拒絕大量的跳轉,這使得收斂到平穩分布的速度太慢。有沒有辦法提升接受率呢?
我們回到MCMC采樣的細緻平穩條件:
p(i)q(i,j)α(i,j)=p(j)q(j,i)α(j,i) p ( i ) q ( i , j ) α ( i , j ) = p ( j ) q ( j , i ) α ( j , i )
我們采樣效率低的原因是 α(i,j)α(i,j) α ( i , j ) α ( i , j ) 太小了,比如為 α(j,i)為0.1,而α(j,i) α ( j , i ) 為 0.1 , 而 α ( j , i ) 為0.2。即:
p(i)q(i,j)∗0.1=p(j)q(j,i)∗0.2 p ( i ) q ( i , j ) ∗ 0.1 = p ( j ) q ( j , i ) ∗ 0.2
這時我們可以看到,如果兩邊同時擴大五倍,接受率提高到了0.5,但是細緻平穩條件卻仍然是滿足的,即:
p(i)q(i,j)∗0.5=p(j)q(j,i)∗0.2 p ( i ) q ( i , j ) ∗ 0.5 = p ( j ) q ( j , i ) ∗ 0.2
這樣我們的接受率可以做如下改進,即:
α(i,j)=min{p(j)q(j│i)p(i)p(i│j),1} α ( i , j ) = m i n { p ( j ) q ( j │ i ) p ( i ) p ( i │ j ) , 1 }
此時便得到了常見的 Metropolis−Hastings M e t r o p o l i s − H a s t i n g s 采樣算法。
步驟
(1)初始化馬氏鍊初始狀态 X0=x0 X 0 = x 0
(2)對 t=0,1,2,3,… t = 0 , 1 , 2 , 3 , … 循環一下過程進行采樣:
第t時刻馬氏鍊狀态為 Xt=xt X t = x t ,采樣 y∼q(x|x(t)) y ∼ q ( x | x ( t ) ) ;
從均勻分布采樣 u∼Uniform[0,1]; u ∼ U n i f o r m [ 0 , 1 ] ;
如果 u<α(xt,y)=min{p(j)q(j│i)p(i)p(i│j),1} u < α ( x t , y ) = m i n { p ( j ) q ( j │ i ) p ( i ) p ( i │ j ) , 1 } ,則接受 xt→y x t → y ,即 xt+1→y x t + 1 → y ;否則不接受機率轉移,即 Xt+1=xt。 X t + 1 = x t 。
以上M-H算法隻針對低維的情況,對于高維情況,我們采用Gibbs采樣。
(六)Gibbs采樣
對于高維情況,我們采用Gibbs采樣。
以二維為例,假設 p(x,y) p ( x , y ) 是一個二維聯合資料分布,考察x坐标相同的兩個點 A(x1,y1)和B(x1,y2) A ( x 1 , y 1 ) 和 B ( x 1 , y 2 ) ,容易發現下面兩式成立:
p(x1,y1)p(y2│x1)=p(x1)p(y1│x1)p(y2|x1) p ( x 1 , y 1 ) p ( y 2 │ x 1 ) = p ( x 1 ) p ( y 1 │ x 1 ) p ( y 2 | x 1 )
p(x1,y2)p(y1│x1)=p(x1)p(y2│x1)p(y1|x1) p ( x 1 , y 2 ) p ( y 1 │ x 1 ) = p ( x 1 ) p ( y 2 │ x 1 ) p ( y 1 | x 1 )
是以得到: p(x1,y1)p(y2│x1)=p(x1,y2)p(y1│x1) p ( x 1 , y 1 ) p ( y 2 │ x 1 ) = p ( x 1 , y 2 ) p ( y 1 │ x 1 )
即: p(A)p(y2│x1)=p(B)p(y1│x1) p ( A ) p ( y 2 │ x 1 ) = p ( B ) p ( y 1 │ x 1 )
觀察上式再觀察細緻平穩條件的公式,我們發現在 x=x1 x = x 1 這條直線上,如果用條件機率分布 p(y|x1) p ( y | x 1 ) 作為馬爾科夫鍊的狀态轉移機率,則任意兩個點之間的轉移滿足細緻平穩條件!
同樣 ,y=y1 , y = y 1 這條直線上,取兩點 A(x1,y1),C(x2,y1) A ( x 1 , y 1 ) , C ( x 2 , y 1 ) 也有如下等式:

基于上面的發現,我們可以構造平面上兩點之間的轉移機率矩陣Q:
Q(A→B)=p(yB│x1)ifxA=xB=x1 Q ( A → B ) = p ( y B │ x 1 ) i f x A = x B = x 1
Q(A→C)=p(xc│x1)ifyA=yc=y1 Q ( A → C ) = p ( x c │ x 1 ) i f y A = y c = y 1
Q(A→D)=0otherwise Q ( A → D ) = 0 o t h e r w i s e
有了上面這個狀态轉移矩陣,我們很容易驗證平面上的兩點X,Y,滿足細緻平穩條件。
p(X)Q(X→Y)=p(Y)Q(Y→X) p ( X ) Q ( X → Y ) = p ( Y ) Q ( Y → X )
于是這個二維空間上的馬氏鍊收斂到平穩分布 p(x,y). p ( x , y ) . 于是可以得到二維Gibbs采樣的步驟:
随機初始化 X0=x0,Y0=y0 X 0 = x 0 , Y 0 = y 0
對 t=0,1,2,‘‘‘‘ t = 0 , 1 , 2 , ‘ ‘ ‘ ‘ 循環采樣:
y(t+1)∼p(y|xt); y ( t + 1 ) ∼ p ( y | x t ) ;
x(t+1)∼p(x|y(t+1)); x ( t + 1 ) ∼ p ( x | y ( t + 1 ) ) ;
以上采樣,馬氏鍊的轉移隻是輪換的沿着坐标軸x軸和y軸做轉移,于是得到樣本 (x0,y0),(x0,y1),(x1,y1),(x1,y2),(x2,y2),…, ( x 0 , y 0 ) , ( x 0 , y 1 ) , ( x 1 , y 1 ) , ( x 1 , y 2 ) , ( x 2 , y 2 ) , … , 馬氏鍊收斂以後得到的樣本就是P(x,y)的樣本了。但其實坐标軸輪換不是強制要求的最一般的情形可以是,在t時刻,可以在x軸和y軸之間随機的選一個坐标軸,然後按條件機率轉移,馬氏鍊一樣可以收斂。輪換兩個坐标軸隻是一種簡便形式。
以上二維推廣到高維的情形,即 x1變到多元x1 x 1 變 到 多 維 x 1 ,推導過程不變,細緻平穩條件依然成立:
p(x1,y1)p(y2│x1)=p(x1,y2)p(y1│x1) p ( x 1 , y 1 ) p ( y 2 │ x 1 ) = p ( x 1 , y 2 ) p ( y 1 │ x 1 )
此時轉移矩陣Q由條件分布 p(y│x1) p ( y │ x 1 ) 定義。
Gibbs采樣步驟
(1)随機初始化{x_i:i=1,…,n}
(2)對t=0,1,2,….循環采樣:
x1(t+1)∼p(x1|xt)2,x(t)3,…,x(t)n) x 1 ( t + 1 ) ∼ p ( x 1 | x 2 t ) , x 3 ( t ) , … , x n ( t ) )
x(t+1)2∼p(x2|x(t+1)1,x(t)3,…,x(t)n) x 2 ( t + 1 ) ∼ p ( x 2 | x 1 ( t + 1 ) , x 3 ( t ) , … , x n ( t ) )
⋅⋅⋅ · · ·
x(t+1)j∼p(xj|x(t+1)2,...,x(t+1)j−1,x(t)j,…,x(t)n) x j ( t + 1 ) ∼ p ( x j | x 2 ( t + 1 ) , . . . , x j − 1 ( t + 1 ) , x j ( t ) , … , x n ( t ) )
⋅⋅⋅ · · ·
x(t+1)n∼p(xn|x(t+1)1,x(t+1)2,…,x(t+1)n−1) x n ( t + 1 ) ∼ p ( x n | x 1 ( t + 1 ) , x 2 ( t + 1 ) , … , x n − 1 ( t + 1 ) )
二、主題模型與MCMC采樣
回顧一下主題模型步驟:
0、 首先随機地給每個詞配置設定一個主題,之後按以下1、2步驟更新主題;
求某一個詞 wi w i 對應主題特征z_i的條件機率分布 p(zi=k|w⃗ ,z⃗ −i) p ( z i = k | w → , z → − i ) 。其中, z⃗ −i z → − i 代表去掉下标為i的詞後的主題分布。
條件機率分布 p(zi=k|w⃗ ,z⃗ −i) p ( z i = k | w → , z → − i ) ,我們就可以進行Gibbs采樣,最終在Gibbs采樣收斂後得到第i個詞的主題。
采樣得到了所有詞的主題,那麼通過統計所有詞的主題計數,就可以得到各個主題的詞分布。
接着統計各個文檔對應詞的主題計數,就可以得到各個文檔的主題分布。
在上一節介紹LDA主題模型的時候得到了生成整個語料庫的聯合分布機率。我們知道,在機率論中,如果得到了聯合分布,則能很輕易地得到條件分布、邊緣分布。那麼今天我們就由聯合分布
去求條件分布 p(zi=k|w⃗ ,z⃗ −i) p ( z i = k | w → , z → − i )
求解條件分布 p(zi=k|w⃗ ,z⃗ −i) p ( z i = k | w → , z → − i )
對于下标i,由于它對應的詞wi是可以觀察到的,是以, p(zi=k|w⃗ ,z⃗ −i)∝p(zi=k,wi=t|w⃗ −i,z⃗ −i) p ( z i = k | w → , z → − i ) ∝ p ( z i = k , w i = t | w → − i , z → − i ) ,對于 zi=k,wi=t, z i = k , w i = t , 它隻涉及到第d篇文檔和第k個主題兩個Dirichlet-multi共轭,即:
于是有:
再由Dirichlet期望公式可得:
有了這個公式,我們就可以用Gibbs采樣去采樣所有詞的主題,當Gibbs采樣收斂後,即得到所有詞的采樣主題。采樣得到了所有詞的主題,那麼通過統計所有詞的主題計數,就可以得到各個主題的詞分布。接着統計各個文檔對應詞的主題計數,就可以得到各個文檔的主題分布。
應用于LDA的Gibbs采樣算法流程:
1)選擇合适的主題數K, 選擇合适的超參數向量α,η
2) 對應語料庫中每一篇文檔的每一個詞,随機的賦予一個主題編号z
3) 重新掃描語料庫,對于每一個詞,利用Gibbs采樣公式更新它的topic編号,并更新語料庫中該詞的編号。
4) 重複第2步的基于坐标軸輪換的Gibbs采樣,直到Gibbs采樣收斂。
5) 統計語料庫中的各個文檔各個詞的主題,得到文檔主題分布θ_d,統計語料庫中各個主題詞的分布,得到LDA的主題與詞的分布β_k。
參考文獻:
部落格:http://blog.csdn.net/u010159842/article/details/48637095
https://www.cnblogs.com/pinard/p/6867828.html
http://blog.csdn.net/baimafujinji/article/details/51407703
《LDA數學八卦》