回歸分析是一種非常廣泛使用的統計工具,用于建立兩個變量之間的關系模型。這些變量之一稱為預測變量,其值通過實驗收集。另一個變量稱為響應變量,其值從預測變量派生。
線上性回歸中,這兩個變量通過方程相關,其中這兩個變量的指數(幂)為1.數學上,線性關系表示當繪制為曲線圖時的直線。任何變量的指數不等于1的非線性關系将建立一條曲線。
線性回歸的一般數學方程為 -
y = ax + b
以下是所使用的參數的描述 -
- y是響應變量。
- x是預測變量。
- a和b被稱為系數常數。
建立回歸的步驟
回歸的簡單例子是當人的身高已知時預測人的體重。為了做到這一點,我們需要有一個人的身高和體重之間的關系。
建立關系的步驟是 -
- 進行收集高度和相應重量的觀測值的樣本的實驗。
- 使用R語言中的lm()函數建立關系模型。
- 從建立的模型中找到系數,并使用這些建立數學方程
- 獲得關系模型的摘要以了解預測中的平均誤差。也稱為殘差。
- 為了預測新人的體重,使用R中的predict()函數。
輸入資料
下面是代表觀察的樣本資料 -
# Values of height151, 174, 138, 186, 128, 136, 179, 163, 152, 131# Values of weight.63, 81, 56, 91, 47, 57, 76, 72, 62, 48
LM()函數
此函數建立預測變量和響應變量之間的關系模型。
文法
線性回歸中lm()函數的基本文法是 -
lm(formula,data)
以下是所使用的參數的說明 -
- 公式是表示x和y之間的關系的符号。
- 資料是應用公式的向量。
建立關系模型并擷取系數
x y # Apply the lm() function.relation print(relation)
當我們執行上面的代碼,它産生以下結果 -
Call:lm(formula = y ~ x)Coefficients:(Intercept) x -38.4551 0.6746
擷取相關的摘要
x y # Apply the lm() function.relation print(summary(relation))
當我們執行上面的代碼,它産生以下結果 -
Call:lm(formula = y ~ x)Residuals: Min 1Q Median 3Q Max-6.3002 -1.6629 0.0412 1.8944 3.9775Coefficients: Estimate Std. Error t value Pr(>|t|)(Intercept) -38.45509 8.04901 -4.778 0.00139 **x 0.67461 0.05191 12.997 1.16e-06 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 3.253 on 8 degrees of freedomMultiple R-squared: 0.9548, Adjusted R-squared: 0.9491F-statistic: 168.9 on 1 and 8 DF, p-value: 1.164e-06
predict()函數
文法
線性回歸中的predict()的基本文法是 -
predict(object, newdata)
以下是所使用的參數的描述 -
- object是已使用lm()函數建立的公式。
- newdata是包含預測變量的新值的向量。
預測新人的體重
# The predictor vector.x # The resposne vector.y # Apply the lm() function.relation # Find weight of a person with height 170.a result print(result)
當我們執行上面的代碼,它産生以下結果 -
1
76.22869
以圖形方式可視化回歸
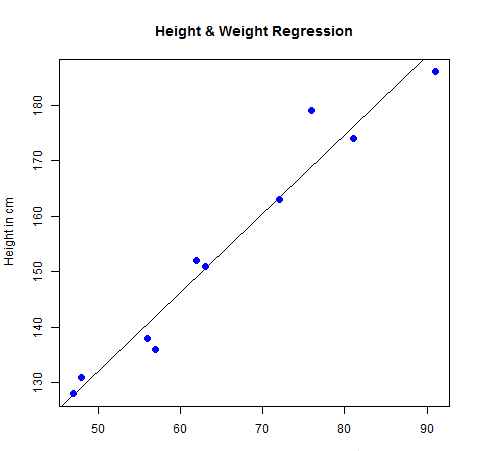
# Create the predictor and response variable.x 151, y 63, relation # Give the chart file a name.png(file = "linearregression.png")# Plot the chart.plot(y,x,col = "blue",main = "Height & Weight Regression",abline(lm(x~y)),cex = 1.3,pch = 16,xlab = "Weight in Kg",ylab = "Height in cm")# Save the file.dev.off()
當我們執行上面的代碼,它産生以下結果 -