目前還在學習階段,是以關于DCP可以參考知乎的一篇問答:https://www.zhihu.com/question/49902644 本文的斜體是可以在CVX的document中找到的,下面就不一一說明了。
CVX強制遵守紀律( disciplined )凸程式設計規則集或DCP規則集的約定。 每當遇到任何規則違規時,CVX都會發出一條錯誤消息,是以在開始構模組化型之前,了解它們是非常重要的。 規則是從凸分析的基本原理繪制的,并且一旦您已經接觸到凸分析和凸優化,便于學習。
DCP規則集是凸性的一組充分條件,但不是必需條件。 是以有可能構造違反規則集的表達式,但實際上是凸的。 作為例子,考慮熵函數,
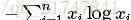
,其定義為x> 0,這是凹的。 如果它被表示為
- sum( x .* log( x ) )
CVX會拒絕它,因為它的凹陷不符合任何構圖規則(composition rules)。 (具體來說,它違反了 Expression rules中描述的無産品規則。)然而,涉及熵的問題可以通過明确地使用熵函數來解決,
它位于基本的CVX庫中,是以被CVX識别為凹面。 如果一個凸(或凹)函數沒有被CVX識别為凸或凹,它可以作為一個新的原子加入; 請參閱将新功能添加到原子庫。
作為另一個例子,考慮函數
,它是凸的。 如果寫成
(假設x是一個标量變量或仿射表達式),它将被CVX識别為一個凸表達式,是以可以用在(适當的)限制和目标中。 但如果寫成
sqrt( x^2 + 1 )
CVX将拒絕它,因為這個函數的凸性并不遵循CVX規則集。
曲率分類
在有規律的凸規劃中,标量表達式按其曲率分類。 有四類曲率:常數,仿射,凸和凹。 對于在所有Rn上定義的函數
,類别具有以下含義:
當然,這些類别有重大的重疊。 例如,常量表達式也是仿射的,并且(實)仿射表達式是凸和凹的。
凸和凹表達式根據定義是真實的。 可以構造複常量和仿射表達式,但是它們的使用更有限; 例如,它們不能出現在不等式限制的左側或右側。
頂級規則
CVX支援三種不同類型的紀律凸面程式:
最小化問題,由一個凸目标函數和零個或多個限制組成。
最大化問題,由一個凹目标函數和零個或多個限制組成。
一個可行性問題,由一個或多個限制和沒有目标組成
限制
有紀律的凸面程式可以指定三種類型的限制:
使用==構造的等式限制,其中雙方都是仿射的。
小于不等式限制,使用<=,其中左側是凸的,右側是凹的。
大于不等式限制,使用> =,其中左側是凹的,右側是凸的。
不允許使用〜=構造的不等式限制。 (這種限制不是凸的。)
平等限制的一方或雙方可能是複雜的; 另一方面,不平等限制必須是實的。 複雜的等式限制相當于兩個實際的等式限制,一個是實部,另一個是虛部。 具有實邊和複邊的等式限制具有将複邊的虛部限制為零的效果。
正如“內建員資格”中所讨論的,CVX使用等式限制來強化集合成員限制(例如,x∈S)。 平等限制的雙方必須仿射的規則也适用于設定成員限制。 實際上,像semidefinite()和lorentz()這樣的集合原子的傳回值是仿射的,是以僅僅驗證集合成員限制的剩餘部分就足夠了。 對于像{x,y}這樣的複合值,每個元素必須是仿射的。
嚴格的不平等
正如在限制中提到的,嚴格不等式<,>被解釋為與非嚴格不等式> =,<=相同的方式。 重要的是要注意,CVX不能保證在計算的解決方案中嚴格滿足不等式。 這不僅僅是我們在CVX上做出的選擇, 這是基礎數學和凸優化求解器設計的自然結果。 是以,我們強烈建議不要在CVX中使用嚴格的不平等,未來的版本可能會将其徹底清除。
嚴格的不平等對于您的模型至關重要時,您可能需要采取額外措施來確定合規性。 在某些情況下,這可以通過标準化來完成。 例如,考慮一組齊次方程和不等式:
除了嚴格的不等式,x = 0将是一個可接受的解決方案; 事實上,避免起源的必要性是嚴重不平等的根本原因。 但是,請注意,如果給定的xx滿足這些限制條件,那麼αx對于所有α> 0也是如此。 通過消除這種正常化的自由度,我們可以消除嚴格的不平等; 例如:
如果規範化對于你的模型不是一個有效的方法,你可能隻需要通過增加一個小的偏移量來将嚴格的不等式轉換成非嚴格的不等式。 例如将x> 0轉換成比如x> = 1e-4。 請注意,界限必須足夠大,以便底層解算器認為它在數值上很重要。
最後,請注意,對于具有由嚴格不等式定義的域的log(x)和inv_pos(x)等函數,域限制由函數本身處理。 您不需要為模型添加明确的限制x> 0來保證解決方案是正确的。
表達規則
到目前為止,所述的規則并沒有特别的限制,因為所有凸面的程式(有紀律的或其他的)通常都遵守它們。 有紀律的凸面程式設計與更一般的凸面程式設計的差別在于管理在目标函數和限制中使用的表達式的構造的規則。
受訓凸程式設計通過遞歸地應用以下規則來确定标量表達式的曲率。 雖然這個清單可能看起來很長,但大多數情況下,凸數分析的基本規則的列舉是凸,凹和仿射形式的組合:和,乘以标量等等。
1、一個有效的常量表達式是
任何形式良好的Matlab表達式,評估為有限的值。
2、一個有效的仿射表達式是
一個有效的常量表達式
一個聲明的變量;
有效地調用原子庫中具有仿射結果的函數;
仿射表達式的總和或差别;
仿射表達式和常量的乘積。
3、一個有效的凸表達式是
一個有效的常量或仿射表達式;
一個有效的調用函數在原子庫中的凸結果;
一個仿射标量上升到一個恒定的功率p≥1,p≠3,5,7,9,…
一個凸的标量二次形式 - 見标量二次形式;
兩個或多個凸表達式的總和;
凸表達式和凹表達式之間的差別;
凸表達式和非負常數的乘積;
凹表達與非正定常數的乘積;
否定的凹面表達。
4、一個有效的凹面表達式是
一個有效的常量或仿射表達式;
對原子庫中的函數進行有效的調用,結果為凹形;
p∈(0,1)的凹标量;
一個凹标量二次形式 - 見标量二次形式;
兩個或多個凹面表情的總和;
凹表達式和凸表達式之間的差異;
凹表示和非負常數的乘積;
凸表達式與非正定常數的乘積;
否定凸表達式。
如果一個表達式不能被這個規則集分類,它将被CVX拒絕。 對于矩陣和數組表達式,這些規則是以元素為基礎應用的。 我們注意到上面列出的規則是多餘的; 有相當小的一套規則。
特别值得注意的是,這些表達規則通常禁止非恒定表達式之間的産品,除了标量二次形式。 例如,表達式x * sqrt(x)恰好是x的一個凸函數,但是它的凸性不能使用CVX規則集來驗證,是以被拒絕。 (然而,它可以表示為pow_p(x,3/2))。我們稱之為無産品規則,密切關注它會大大地保證你構造的表達式是有效的。
函數
在CVX中,函數被分為兩個屬性:曲率(常量,仿射,凸或凹)和單調性(非遞減,非遞增或非單調)。 曲率根據上面給出的表達式确定它們可以在表達式中出現的條件。 單調性決定了它們如何用于函數組合中,我們将在下一節中看到。
對于隻有一個參數的函數,分類很簡單。 下表給出了一些例子。
根據凸分析的标準實踐,當參數在函數域外時,凸函數被解釋為+∞,當參數在域外時,凹函數被解釋為-∞。 換句話說,CVX中的凸函數和凹函數被解釋為它們的擴充值擴充。
這具有自動限制函數的參數在函數的域中的效果。 例如,如果我們在一個CVX規範中構造sqrt(x + 1),其中x是一個變量,那麼x将被自動限制為大于或等于-1-1。 沒有必要添加一個單獨的限制,x> = - 1來執行此操作。
函數的單調性在擴充意義上被确定,即包括在其域之外的自變量的值。 例如,sqrt(x)被确定為非遞減的,因為其參數的負值是常數(-∞); 然後在參數為零時跳到0。
即使參數限制在這些部分之一中,CVX也不認為函數是凸或凹的,如果僅僅是它的一部分域的話。 作為一個例子,考慮函數1 / x。 這個函數對于x> 0是凸的,對于x <0是凹的。 但是,即使已經施加了限制條件(如x> = 1),将x限制在函數1 / x的凸起部分,您也不能在CVX中寫入1 / x(除非x是常量)。 你可以使用CVX函數inv_pos(x),定義為1 / x對于x> 0,否則對于凸起部分1 / x定義為∞; CVX認識到這個函數是凸和不增加的。 在CVX中,可以使用-inv_pos(-x)來表示1 / x的凹入部分,其中x是負的,這将被正确識别為凹和不增加。(這段話的意思應該是在CVX中,要整個函數的定義域是凸/凹的,例如1/x在大于零的部分,可以指定x為負時,1/x為∞)。
對于具有多個參數的函數,曲率總是被認為是共同的,但是可以在逐個參數的基礎上考慮單調性。 例如,函數quad_over_lin(x,y)
在x和y中都是共凸的,但是在y中是單調的(不增加)。
一些函數是凸的,凹的,或者仿射它的參數的一個子集。 例如,函數norm(x,p)其中p \ geq 1僅在其第一個參數中是凸的。 無論何時在CVX規範中使用此函數,其餘參數必須是常量,否則CVX将發出錯誤消息。 這些參數對應于數學術語中的函數參數; 例如
是以我們也應該把這樣的論點作為參數在這個範圍内引用。 從此以後,每當我們将CVX函數稱為凸,凹或仿射時,我們将假設其參數是已知的并且已經被給予适當的,恒定的值。
組成
凸分析的一個基本規則是在仿射映射的組合下凸性是封閉的。 這也是DCP規則集的一部分:
凸,凹或仿射函數可以接受仿射表達式(相容大小)作為參數。 結果分别是凸面,凹面或仿射。
例如,考慮在CVX原子庫中提供的函數square(x)。 這個函數對其論點進行了平方 即它計算x * x(對于數組參數,它獨立地對每個元素進行平方)。它在CVX原子庫中,并且已知是凸的,隻要它的參數是實的。 是以如果x是維數n的實變量,則a是一個常數n向量,而b是一個常量,即表達式
會被CVX接受,它知道它是凸的。
上面的仿射合成規則是一個更複雜的合成規則的特例,我們現在描述它。 我們考慮一個具有
已知曲率和單調性的函數,它接受多個參數。 對于凸函數,規則是:
如果函數在參數中不減少,那麼參數必須是凸的。
如果這個函數在一個論證中是不增加的,那麼這個論證就必須是凹的。
如果這個函數在一個論證中既不是非遞減的也不是非遞增的,那麼這個論證必須是仿射的。
如果函數的每個參數滿足這些規則,則表達式被CVX接受,并被分類為凸。 回想一下,常數或仿射表達式既是凸凹的,是以任何參數都可以是仿射的,包括作為特例的常量。
凹函數的相應規則如下:
如果函數在參數中不減少,則該參數必須是凹形的。
如果函數在參數中不增加,則該參數必須是凸的。
如果這個函數在一個論證中既不是非遞減的也不是非遞增的,那麼這個論證必須是仿射的。
在這種情況下,表達式被CVX接受,并被分類為凹面。
有關這些組合規則的更多背景資訊,請參見凸面優化,第3.2.4節。 事實上,除了标量二次表達式之外,整個DCP規則集可以被認為是這六條規則的特例。
讓我們來看一些例子。 最大函數在每個參數中都是凸和不減的,是以它可以接受任何凸的表達式作為參數。 例如,如果x是一個向量變量,那麼
max( abs( x ) )
遵循六個組合規則中的第一個,是以被CVX接受,并被歸類為凸面。 作為另一個例子,考慮和函數,既是凸函數又是凹函數(因為它是仿射的),而且在每個參數中都是非遞減的。 是以表達式
sum( square( x ) )
sum( sqrt( x ) )
在CVX中被認為是有效的,分别被分類為凸和凹。 第一個是凸函數的第一條規則; 第二個是凹函數的第一條規則。
大多數知道基本凸分析的人喜歡用更具體的規則來思考這些例子:凸函數的最大值是凸的,凸(凹)函數的總和是凸的(凹的)。 但是這些規則隻是上面一般構成規則的特例。 一般合成規則中的一些其他衆所周知的基本規則是:
凸(凹)函數的非負多項是凸(凹)的;
凸(凹)函數的非正共轭是凹(凸)的。
現在我們深入考慮一個更複雜的例子。 假設x是一個向量變量,A,b和f是具有适當次元的常量。 CVX識别表達式
sqrt(f'*x) + min(,-norm(A*x-b))
作為凹面。 考慮術語sqrt(f’* x)。 CVX認識到sqrt是凹的,f’* x是仿射的,是以它得出sqrt(f’* x)是凹的。 現在考慮第二項min(4,1.3範數(A * x-b))。 CVX認識到min是凹的而非減的,是以它可以接受凹面的論點。 CVX認識到1.3範數(A * x-b)是凹的,因為它是常數和凸函數的差别。 是以CVX認為第二個詞也是凹的。 整個表達式被認為是凹的,因為它是兩個凹函數的和。
構圖規則(composition rules)是足夠的,但對于分類的正确性來說并不是必須的,是以一些實際上是凸面或凹面的表達将不能滿足它們,是以将被CVX拒絕。 例如,如果x是一個向量變量,則表達式
被CVX拒絕,因為沒有規則來規定具有凸函數的凹非遞減函數的組成。 當然,在這種情況下,解決方法很簡單:使用norm(x),因為norm在原子庫中,并且由CVX知道是凸的。
非線性組合中的單調性
單調性是非線性成分規則的一個重要方面。 這有一些不是很明顯的後果,我們将在這裡舉例說明。 考慮這個表達
其中x是一個标量變量。 這個表達式實際上是凸的,因為
是凸的。 但是CVX會拒絕這個表達式,因為外方不能接受一個凸參數。 事實上,凸函數的平方一般不是凸的:例如,
不是凸的。
有幾種方法可以修改上面的表達式以符合規則集。 一種方法是将其寫為x ^ 4 + 2 * x ^ 2 + 1,CVX認為是凸的,因為CVX允許使用^運算符為正整數。 (請注意,應用于函數
的相同技術将失敗,因為它的第二項是凹的。)
另一種方法是使用代表函數
,其中x + = max {0,x}的可選外部函數square_pos,包含在CVX庫中。 顯然,square和square_pos當它們的參數是非負的時候是重合的。 但是square_pos是非遞減的,是以它可以接受一個凸的參數。 是以,表達
在數學上等同于上面的拒絕版本(因為外部函數的參數總是正數),但它滿足DCP規則集,是以被CVX接受。
這就是CVX原子庫中的幾個函數有兩種形式的原因:“自然”形式,以及被修改為單調的形式,是以可用于合成。 其他這樣的“單調擴充”包括sum_square_pos和quad_pos_over_lin。 如果你正在自己實作一個新的功能,你可能想考慮一下這個功能的單調擴充也是有用的。
标量二次形式
在其純粹形式中,DCP規則集甚至禁止使用簡單的二次表達式,如x * x(假設x是一個标量變量)。 出于實際的原因,我們選擇規則集的一個例外,以允許識别直接映射到CVX原子庫中的某些凸二次函數(或它們的凹面底片)的某些特定的二次形式:
CVX檢測諸如左上方的二次表達式,并确定它們是凸起的還是凹入的; 如果是的話,将它們轉換為等價的函數調用,比如上面的那些。
CVX檢查仿射表達式的每個單一乘積,并且仿射表達式的每一個平方,檢查凸性; 它不會檢查例如仿射表達式的産品的總和。 例如,給定标量變量x和y,表達式
x ^ 2 + 2 * x * y + y ^2
會導緻CVX中的錯誤,因為三個項2 * x * y中的第二個既不是凸的也不是凹的。 但是等同的表達
( x + y ) ^ 2( x + y ) * ( x + y )
會被接受。
當CVX碰到一個标量二次形式時,CVX實際上完成了這個正方形,是以這個形式不需要是對稱的。 例如,如果z是一個向量變量,則a,b是常數,那麼Q是正定的
( z + a )' * Q * ( z + b )
将被識别為凸。 一旦CVX驗證了一個二次形式,它就可以以任何正常的凸或凹表達式的方式自由使用,如表達式規則中所述。
在有紀律的凸規劃中,實際上應該使用較少的二次形式,而不是在更傳統的數學規劃架構中,其中二次形式往往是一個真正希望使用的非光滑形式的平滑替代。 在CVX中,由于支援非平滑函數,是以這種替換很少是必需的。 例如,限制
用歐幾裡得規範等價地表示:
使用現代求解器,第二種形式更自然地使用二階錐限制表示 - 是以第二種形式實際上可能更有效。 事實上,根據我們的經驗,這個非平方的形式往往會被更準确地處理。 是以我們強烈建議您根據紀律凸函數提供的新功能重新評估模型中二次形式的使用。