題目描述:
愛麗絲參與一個大緻基于紙牌遊戲 “21點” 規則的遊戲,描述如下:
愛麗絲以 0 分開始,并在她的得分少于 K 分時抽取數字。 抽取時,她從 [1, W] 的範圍中随機獲得一個整數作為分數進行累計,其中 W 是整數。 每次抽取都是獨立的,其結果具有相同的機率。
當愛麗絲獲得不少于 K 分時,她就停止抽取數字。 愛麗絲的分數不超過 N 的機率是多少?
示例 1:
輸入:N = 10, K = 1, W = 10
輸出:1.00000
說明:愛麗絲得到一張卡,然後停止。
示例 2:
輸入:N = 6, K = 1, W = 10
輸出:0.60000
說明:愛麗絲得到一張卡,然後停止。
在 W = 10 的 6 種可能下,她的得分不超過 N = 6 分。
示例 3:
輸入:N = 21, K = 17, W = 10
輸出:0.73278
提示:
0 <= K <= N <= 10000
1 <= W <= 10000
如果答案與正确答案的誤差不超過 10^-5,則該答案将被視為正确答案通過。
此問題的判斷限制時間已經減少。
來源:力扣(LeetCode)
連結:https://leetcode-cn.com/problems/new-21-game
著作權歸領扣網絡所有。商業轉載請聯系官方授權,非商業轉載請注明出處。
參考這位師兄的部落格,這道題目我是真的沒搞清楚
添加連結描述
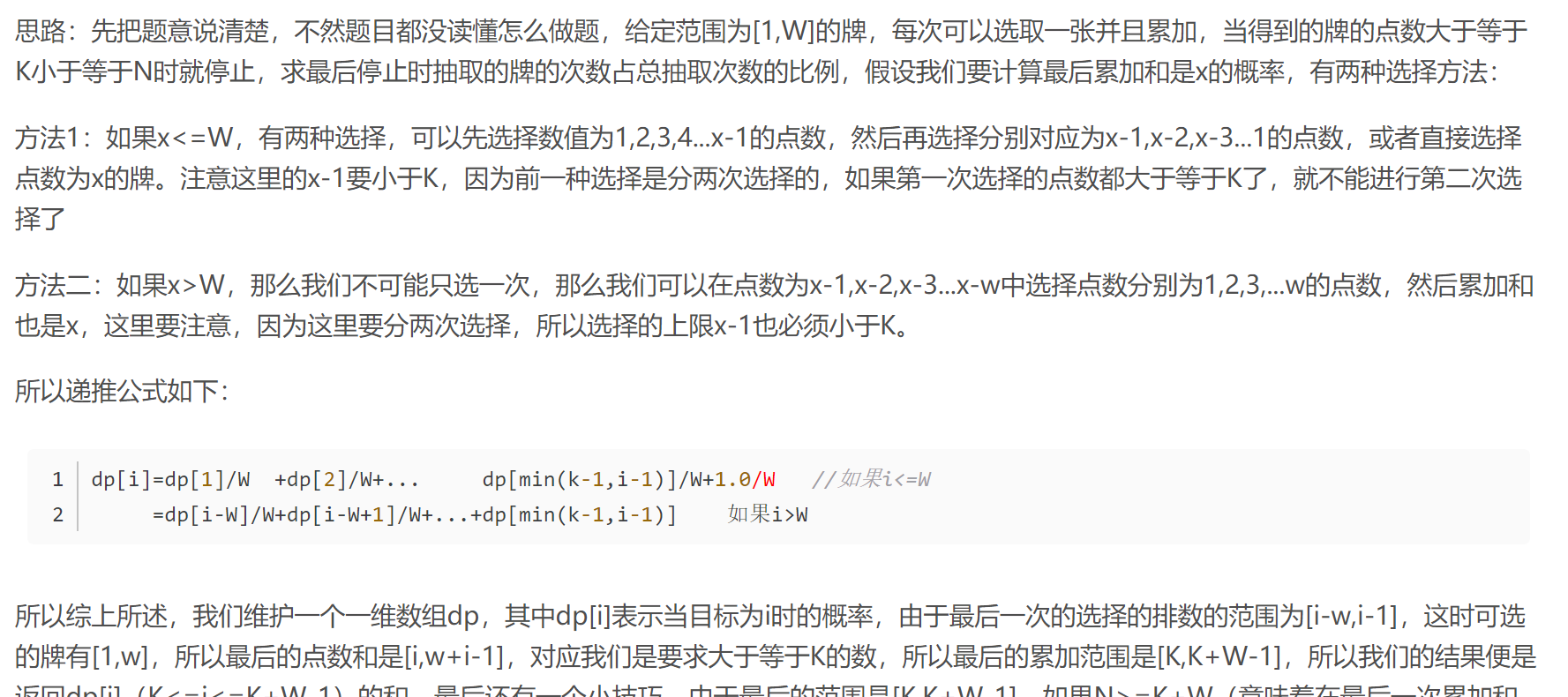
這位兄弟解釋的比較詳細
class Solution {
public:
double new21Game(int N, int K, int W) {
if (K == 0 || N >= (K + W)) return 1.0;
vector<double> dp(N + 1);
double res = 0.0;
double sum = 0.0;
for (int i = 1; i <= N; i++) {
dp[i] = i <= W ? sum / W + 1.0 / W : sum/W; //如遞推公式紅色标出所示,兩種的遞推公式隻有紅色是不一樣的,其餘都是累加前面W項的和
if (i < K) sum += dp[i]; //當i<k時min(k-1,i-1)=i-1,是以繼續累加前面的和,當i>=k時min(k-1,i-1)=k-1,是以就不累加了
if (i > W) sum -= dp[i - W];
if (i >= K) res += dp[i];
}
return res;
}
};