相信大家已經讀過資料科學中 17 種相似性和相異性度量(上),如果你還沒有閱讀,請戳????這裡。本篇将繼續介紹資料科學中 17 種相似性和相異性度量,希望對你有所幫助。
⑦ 皮爾遜相關距離
相關距離量化了兩個屬性之間線性、單調關系的強度。此外,它使用協方內插補點作為初始計算步驟。但是,協方差本身很難解釋,并且不會顯示資料與表示測量之間趨勢的線的接近或遠離程度。
為了說明相關性意味着什麼,回到我們的 Iris 資料集并繪制
Iris-Setosa
樣本以顯示兩個特征之間的關系:花瓣長度和花瓣寬度。
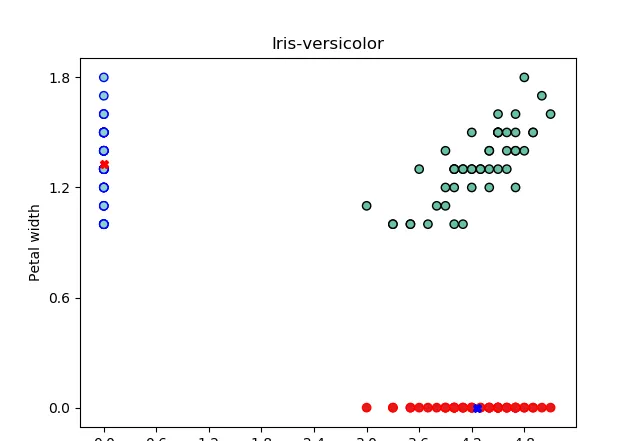
具有兩個特征測量值的 Iris-Setosa 樣本
已估計相同花卉樣本的兩個特征的樣本均值和方差,如下圖所示。
一般來說,我們可以說花瓣長度值相對較低的花的花瓣寬度值也相對較低。此外,花瓣長度值相對較高的花朵也具有花瓣寬度值相對較高的值。此外,我們可以用一條線來總結這種關系。
樣本均值和方差估計
這條線表示花瓣長度和花瓣寬度的值一起增加的積極趨勢。
協方內插補點可以對三種關系進行分類:
三種相關性
相關距離可以使用以下公式計算:
其中分子表示觀測值的協方內插補點,分母表示每個特征方差的平方根。
舉一個簡單的例子來示範我們如何計算這個公式。
紅點和藍點分别具有以下坐标:
A(1.2, 0.6) 和 B (3.0, 1.2)
。
兩次測量的估計樣本均值等于:
該名額的最後一點是相關性并不意味着因果關系。例如,具有相對較小花瓣長度值的
iris-Setosa
并不意味着花瓣寬度值也應該較小。是充分條件但不是必要條件!可以說,小花瓣長度可能導緻小花瓣寬度,但不是唯一的原因!
⑧ 斯皮爾曼相關
與
Pearson
相關性一樣,每當我們處理雙變量分析時,都會使用
Spearman
相關性。但是,與
Pearson
相關性不同,
Spearman
相關性在兩個變量都按等級排序時使用,它可用于分類和數字屬性。
虹膜資料集的相關矩陣
斯皮爾曼相關指數可以使用以下公式計算:
Spearman 相關性常用于假設檢驗。
⑨ 馬氏距離
馬氏距離Mahalanobis是一種主要用于多變量統計測試的度量名額,其中歐氏距離無法給出觀測值之間的實際距離。它測量資料點離分布有多遠。
來自平均值的具有相同 ED 值的兩個點。
如上圖所示,紅點和藍點與均值的歐幾裡得距離相同。但是,它們不屬于同一區域或叢集:紅點更有可能與資料集相似。但是藍色的被認為是異常值,因為它遠離代表資料集中最大可變性方向的線(長軸回歸)。是以,引入了馬哈拉諾比斯度量來解決這個問題。
Mahalanobis 度量試圖降低兩個特征或屬性之間的協方差,因為您可以将之前的圖重新縮放到新軸。并且這些新軸代表特征向量,如前面所示的第一個特征向量。
特征向量的第一個方向極大地影響了資料分類,因為它具有最大的特征值。此外,與其他垂直方向相比,資料集沿該方向展開得更多。
使用這種技術,我們可以沿着這個方向縮小資料集并圍繞均值(PCA)旋轉它。然後我們可以使用歐幾裡得距離,它給出了與前兩個資料點之間的平均值的不同距離。這就是馬哈拉諾比斯名額的作用。
兩個物體 P 和 Q 之間的馬氏距離。
其中C表示屬性或特征之間的協方差矩陣。
為了示範這個公式的用法,我們計算 A(1.2, 0.6) 和 B (3.0, 1.2) 之間的距離,來自之前在相關距離部分的例子。
現在評估協方差矩陣,其定義二維空間中的協方差矩陣如下:
其中 Cov[P,P] = Var[P] 和 Cov[Q,Q]= Var[Q],以及兩個特征之間的協方差公式:
是以,兩個物體 A 和 B 之間的馬哈拉諾比斯距離可以計算如下:
除了其用例之外,馬哈拉諾比斯距離還用于Hotelling t 方檢驗[2]。
⑩ 标準化歐幾裡得距離
标準化或歸一化是在建構機器學習模型時在預處理階段使用的一種技術。該資料集在特征的最小和最大範圍之間存在很大差異。在對資料進行聚類時,此比例距離會影響 ML 模型,進而導緻錯誤的解釋。
例如,假設有兩個不同的特征,它們在範圍變化方面表現出很大差異。例如,假設有一個從 0.1 到 2 變化的特征和另一個從 50 到 200 變化的特征。使用這些值計算距離會使第二個特征更具優勢,進而導緻不正确的結果。換句話說,歐氏距離将受到具有最大值的屬性的高度影響。
這就是為什麼标準化是必要的,以便這些特征以平等地做出貢獻。它是通過将變量轉換為所有具有等于 1 的相同方差并将特征集中在平均值周圍來完成的,如下面的公式所示 Z 分數标準化:
标準化的歐幾裡德距離可以表示為:
可以應用這個公式來計算 A 和 B 之間的距離。
⑪ 卡方距離
卡方距離通常用于計算機視覺中,同時進行紋理分析,以發現歸一化直方圖之間的(不同)相似性,稱為“直方圖比對”。
直方圖比對。資料來源:維基百科直方圖比對[3]
人臉識别算法将是一個很好的例子,它使用這個名額來比較兩個直方圖。例如,在新面孔的預測步驟中,模型根據新捕獲的圖像計算直方圖,将其與儲存的直方圖(通常存儲在 .yaml 檔案中)進行比較,然後嘗試為其找到最佳比對。這種比較是通過計算每對 n 個 bin 的直方圖之間的卡方距離來進行的。
此公式與标準正态分布的卡方統計檢驗不同,後者用于使用以下公式決定是保留還是拒絕原假設:
其中 O 和 E 分别代表觀察到的和預期的資料值。
假設對 1000 人進行了一項調查,以測試給定疫苗的副作用,并檢視是否存在基于性别的顯着差異。是以,每個人都可以是以下四類之一:
1- 男性無副作用。
2- 男性有副作用。
3- 女性無副作用。
4- 有副作用的女性。
零假設是:兩種性别之間的副作用沒有顯着差異。
為了接受或拒絕此假設,可以計算以下資料的卡方檢驗值:
收集的資料
通過将這些值代入卡方檢驗公式,将得到
1.7288
。
使用自由度等于1的卡方表[4],将獲得介于 0.2 和 0.1 > 0.05 之間的機率 → 接受原假設。
請注意,
自由度 =(列數 -1)x(數量或行數 -1)
這裡隻是想讓你快速回顧一下假設檢驗;我希望你覺得這對你有幫助。
⑫Jensen-Shannon 距離
Jensen-Shannon 距離計算兩個機率分布之間的距離。它使用 Kullback Leibler divergence(相對熵)公式來計算距離。
Jensen-Shannon 距離。
其中 R 是 P 和 Q 之間的中點。
此外,隻需簡要說明如何解釋熵的值:
事件A的低熵意味着知道這個事件會發生;換句話說,如果事件 A 會發生,我并不感到驚訝,而且我非常有信心它會發生。高熵的類比相同。
另一方面,Kullback Leibler 散度本身不是距離度量,因為它不是對稱的:。
⑬ 萊文斯坦距離
用于測量兩個字元串之間相似性的度量。它等于将給定字元串轉換為另一個字元串所需的最少操作數。共有三種類型的操作:
- 代換
- 插入
- 删除
對于 Levenshtein 距離,替代成本是兩個機關,另外兩個操作的替代成本是一個。
例如,取兩個字元串
s=“Bitcoin”
和
t=“Altcoin”
。要從 s 到 t,需要用字母
“A”
和
“l”
兩次替換字母
“B”
和
“I”
。是以,
d(t, s) = 2 * 2 = 4
。
Levenshtein 距離有很多用例,如垃圾郵件過濾、計算生物學、彈性搜尋等等。
⑭ 漢明距離
漢明距離等于兩個相同長度的碼字不同的位數。在二進制世界中,它等于兩個二進制消息之間不同位的數量。
例如,可以使用以下方法計算兩條消息之間的漢明距離:
它看起來像分類資料上下文中的曼哈頓距離。
對于長度為 2 位的消息,此公式表示分隔兩個給定二進制消息的邊數。它最多可以等于二。
二維
同樣,對于長度為 3 位的消息,此公式表示分隔兩個給定二進制消息的邊數,它最多可以等于三。
三維
舉一些例子來說明漢明距離是如何計算的:
H(100001, 010001) = 2
H(110, 111) = 1 如果其中一個消息包含全零,則漢明距離稱為漢明權重,等于給定消息中非零數字的數量。在我們的例子中,它等于 1 的總數。
H(110111,000000) = W (110111) = 5 如果可能,漢明距離用于檢測和糾正通過不可靠的噪聲信道傳輸的接收消息中的錯誤。
⑮ 傑卡德/谷本距離
用于衡量兩組資料之間相似性的名額。有人可能會争辯說,為了衡量相似性,需要計算兩個給定集合之間的交集的大小(基數、元素數)。
然而,僅憑公共元素的數量并不能告訴我們它與集合大小的相對關系。這就是 Jaccard 系數背後的直覺。
是以Jaccard提出,為了衡量相似度,你需要用交集的大小除以兩組資料的并集的大小。
傑卡德距離
Jaccard 距離與 Jaccard 系數互補,用于衡量資料集之間的差異,計算公式為:
下圖說明了如何将此公式用于非二進制資料的Jaccard 索引示例。
對于二進制屬性,Jaccard 相似度使用以下公式計算:
Jaccard 索引可用于某些領域,如語義分割、文本挖掘、電子商務和推薦系統。
現在你可能會想:“好吧,但你剛才提到餘弦距離也可以用于文本挖掘。你更喜歡使用什麼作為給定聚類算法的度量?無論如何,這兩個名額之間有什麼差別?”
很高興你問了這個問題。為了回答這個問題,我們需要比較兩個公式的每一項。
Jaccard 和餘弦公式
這兩個公式之間的唯一差別是分母項。不是用 Jaccard 計算兩個集合之間的聯合大小,而是計算 P 和 Q 之間點積的大小。而不是在 Jaccard 公式的分母中添加項;你正在計算餘弦公式中兩者之間的乘積。我不知道那是什麼解釋。據我所知,點積告訴我們一個向量在另一個方向上有多少。除此之外,如果有什麼要補充的,可在評論區給我留言。
⑯ Sørensen–Dice
Sørensen-Dice 距離是一種統計名額,用于衡量資料集之間的相似性。它被定義為 P 和 Q 的交集大小的兩倍,除以每個資料集 P 和 Q 中元素的總和。
Sørensen–Dice 系數。
與 Jaccard 一樣,相似度值的範圍從零到一。但是,與 Jaccard 不同的是,這種相異性度量不是度量标準,因為它不滿足三角不等式條件。
Sørensen–Dice 用于詞典編纂[5]、圖像分割[6]和其他應用程式。
????Pydist2
pydist2是一個python包,1:1代碼采用pdist[7]和pdist2[8] Matlab函數,用于計算觀測之間的距離。pydist2 目前支援的測量距離的方法清單可在閱讀文檔中找到[9]。
from pydist2.distance import pdist1, pdist2
import numpy as np
x = np.array([[1, 2, 3],
[7, 8, 9],
[5, 6, 7],], dtype=np.float32)
y = np.array([[10, 20, 30],
[70, 80, 90],
[50, 60, 70]], dtype=np.float32)
a = pdist1(x)
a
>>> array([10.39230485, 6.92820323, 3.46410162])
pdist1(x, 'seuclidean')
>>> array([3.40168018, 2.26778677, 1.13389339])
pdist1(x, 'minkowski', exp=3)
>>> array([8.65349742, 5.76899828, 2.88449914])
pdist1(x, 'minkowski', exp=2)
>>> array([10.39230485, 6.92820323, 3.46410162])
pdist1(x, 'minkowski', exp=1)
>>> array([18., 12., 6.])
pdist1(x, 'cityblock')
>>> array([18., 12., 6.])
pdist2(x, y)
>>> array([[ 33.67491648, 135.69819453, 101.26203632],
... [ 24.37211521, 125.35549449, 90.96153033],
... [ 27.38612788, 128.80217389, 94.39279634]])
pdist2(x, y, 'manhattan')
>>> array([[ 54., 234., 174.],
... [ 36., 216., 156.],
... [ 42., 222., 162.]])
pdist2(x, y, 'sqeuclidean')
>>> array([[ 1134., 18414., 10254.],
... [ 594., 15714., 8274.],
... [ 750., 16590., 8910.]])
pdist2(x, y, 'chi-squared')
>>> array([[ 22.09090909, 111.31927838, 81.41482329],
... [ 8.48998061, 88.36363636, 59.6522841 ],
... [ 11.75121275, 95.51418525, 66.27272727]])
pdist2(x, y, 'cosine')
>>> array([[-5.60424152e-09, 4.05881305e-02, 3.16703408e-02],
... [ 4.05880431e-02, 7.31070616e-08, 5.62480978e-04],
... [ 3.16703143e-02, 5.62544701e-04, -1.23279462e-08]])
pdist2(x, y, 'earthmover')
>>> array([[ 90., 450., 330.],
... [ 54., 414., 294.],
... [ 66., 426., 306.]]) ???? 寫在最後
這裡已到達本文的結尾,本次内容已經分享結束了,在本文中,你了解了資料科學中使用的不同類型的名額及其在許多領域的應用。如果你有什麼想說的,請盡管在文末留言區留言!
參考資料
[1]
參考原文: https://towardsdatascience.com/17-types-of-similarity-and-dissimilarity-measures-used-in-data-science-3eb914d2681
[2]
Hotelling t 方檢驗: https://en.wikipedia.org/wiki/Hotelling's_T-squared_distribution
[3]
維基百科直方圖比對: https://en.wikipedia.org/wiki/Histogram_matching
[4]
卡方表: https://www.statology.org/wp-content/uploads/2020/01/chi_square_table_small.jpg
[5]
詞典編纂: https://en.wikipedia.org/wiki/Lexicography
[6]
圖像分割: https://en.wikipedia.org/wiki/Image_segmentation
[7]
pdist: https://www.mathworks.com/help/stats/pdist.html
[8]
pdist2: https://www.mathworks.com/help/stats/pdist2.html
[9]