文章目錄
- 1、概述
- 2、十大算法性能比較
- 3、排序算法精講
-
- 3.1 超級經典的排序——冒泡排序和它的優化
- 3.2 最常用的排序——快速排序(基準值分段,交換,分而治之,遞歸實作)
- 3.3 最簡單直接的排序——直接選擇排序(挑最大/最小的那個)
- 3.4 看起來好煩的排序——堆排序(間接選擇排序、完全二叉樹)
- 3.5 分治法的典型應用——歸并排序(分治遞歸)
- 3.6 跟打牌一樣的排序——插入算法(每個數都找到它應該插入的位置)
- 3.7 改進直接插入排序的排序——希爾排序(縮小增量排序,Δ牛筆)
- 3.8 傳說中時間複雜度為O(n)的排序——計數排序(非比較穩定排序)
- 3.9 快快快的桶裝資料排序——桶排序(利用了快排的特性和計數裡的類似映射)
- 3.10 每次都看位數值的排序——基數排序(利用了桶,基數對應進制)
- 4、總結
1、概述
十種常見排序算法可以分為兩大類:
-
比較類排序
-
非比較類排序
:不通過比較來決定元素間的相對次序,它可以突破基于比較排序的時間下界,以線性時間運作,是以也稱為線性時間非比較類排序。
如圖所示
一些概念小結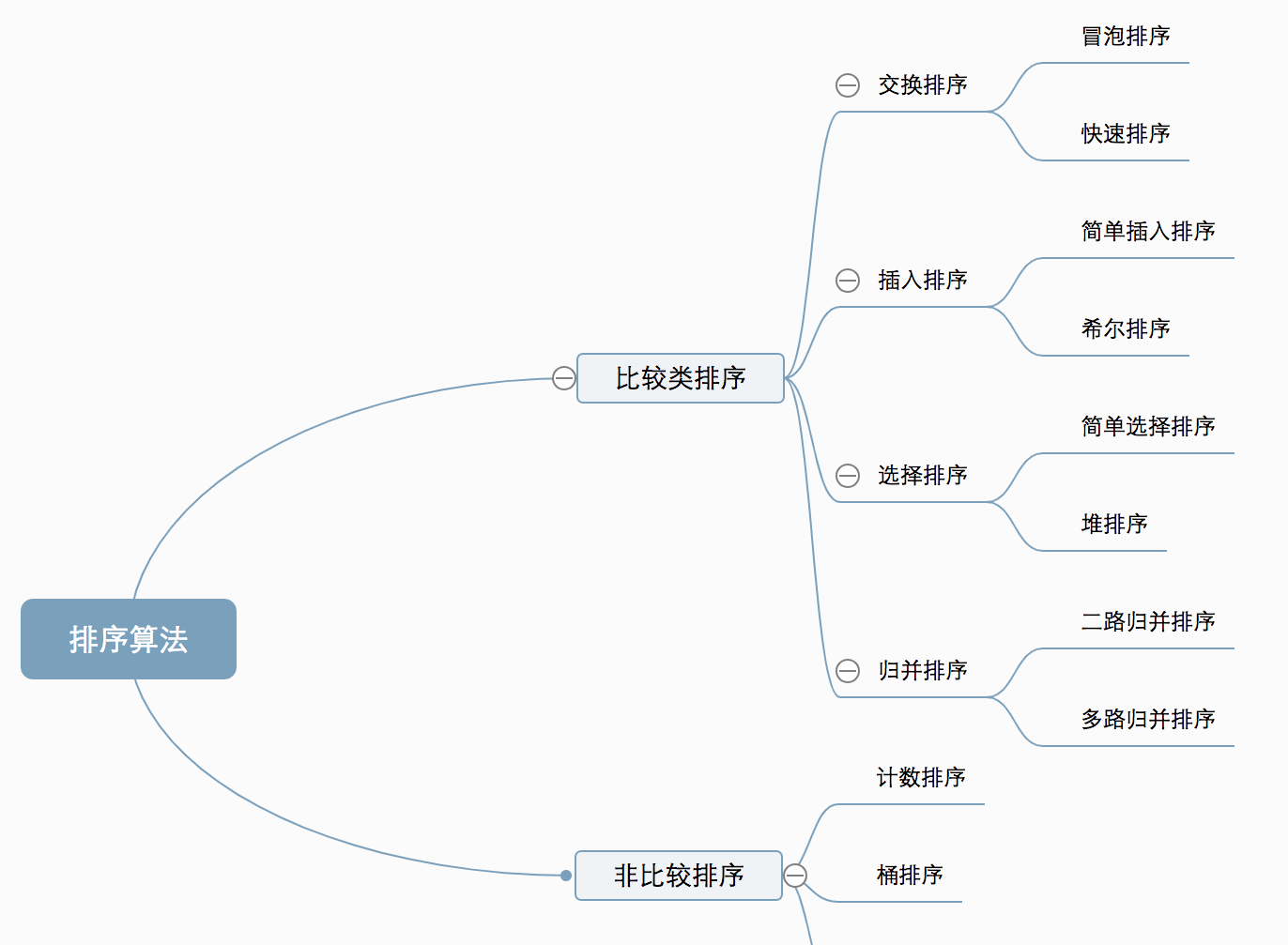
一點就懂的經典十大排序算法1、概述2、十大算法性能比較3、排序算法精講4、總結 - 穩定性判斷:假定在待排序的記錄序列中,存在多個具有相同的關鍵字的記錄,
若經過排序,這些記錄的相對次序保持不變,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序後的序列中,r[i]仍在r[j]之前,則稱這種排序算法是穩定的;否則稱為不穩定的。
- 時間複雜度:對排序資料的總的操作次數。反映當n變化時,操作次數呈現什麼規律。使用大O估計法
- 空間複雜度:是指算法在計算機内執行時所需存儲空間的度量,它也是資料規模n的函數。使用大O估計法
關于穩定性:
需要注意的是,排序算法是否為穩定的是由具體算法決定的,不穩定的算法在某種條件下可以變為穩定的算法,而穩定的算法在某種條件下也可以變為不穩定的算法。
2、十大算法性能比較
3、排序算法精講
3.1 超級經典的排序——冒泡排序和它的優化
1)原理
n個元素的序列,從第一個數開始,每次比較相鄰的兩個數,如果符合
a[j]<a[j+1]
,就交換,直到把目前的最大數“冒泡”到最上面,我們完成一輪的冒泡趟數;
每一輪冒泡趟數,找到最大的那個數放到數組最後面,然後接着對剩下的n-1個數進行下一輪的冒泡。
這樣總共要
冒泡 n-1趟
2)代碼實作(java)
public static void bubbleSort(int[]array,boolean exchange) {//重載,exchange标志表示為升序排序還是降序排序
for (int i =1; i < array.length; i++)//控制次數,第幾趟排序,隻需要n-1趟
{
for (int j = 0; j < array.length - i; j++)//i表示進行的趟數,每一趟能排好一個數,隻需要排剩下的array.length-i個數
if (exchange ? array[j] > array[j + 1] : array[j] < array[j + 1])//控制升序還是降序
{
int temp = array[j];
array[j]=arrjay[j+1];
array[j+1]=temp;//交換兩個數
}
}
}
3)優化
我們知道每一趟的進行,隻是為了把目前的最大的數冒泡上去,那如果目前趟數的最大數本身就是在數組的最右邊(即本身已經冒泡好了),那我們何必繼續該輪冒泡呢?基于這一點,我們可以推出:上一輪沒有發生交換,說明資料的順序已經排好,沒有必要繼續進行下去。
解決辦法:
加一個标志位,記錄上一次是否發生了交換,如果是,我們則進行下一輪,如果沒有,說明已經冒泡好了
代碼實作:
public static void bubbleSort(int[]array,boolean exchange) {//重載,exchange标志表示為升序排序還是降序排序
boolean flag = true;
for (int i =1; i < array.length&&flag; i++)//控制次數,第幾趟排序,隻需要n-1趟,有交換時進行,隻有flag=false就說明上一次一個元素都沒有進行交換
{
flag = false;//假定未交換
for (int j = 0; j < array.length - i; j++)//i表示進行的趟數,每一趟能排好一個數,隻需要排剩下的array.length-i個數
if (exchange ? array[j] > array[j + 1] : array[j] < array[j + 1])//控制升序還是降序
{
int temp = array[j];
array[j]=arrjay[j+1];
array[j+1]=temp;//交換兩個數
flag = true;//記錄是否發生交換,
}
}
}
4)Demo示範
原算法:
優化以後:
5)評價
它的時間複雜度達到了
O(N2)
。這是一個非常高的時間複雜度。冒泡排序早在 1956 年就有人開始研究,之後有很多人都嘗試過對冒泡排序進行改進,但結果卻令人失望。如 Knuth(Donald E. Knuth 中文名為高德納,1974 年圖靈獎獲得者)所說:“冒泡排序除了它迷人的名字和導緻了某些有趣的理論問題這一事實之外,似乎沒有什麼值得推薦的。” 假如我們的計算機每秒鐘可以運作
10 億次
,那麼對
1 億
個數進行排序,桶排序則隻需要
0.1 秒
,而冒泡排序則需要
1 千萬秒
,達到
115
天之久!有沒有既不浪費空間又可以快一點的排序算法呢?那就是“快速排序”啦!
3.2 最常用的排序——快速排序(基準值分段,交換,分而治之,遞歸實作)
1)原理
設要排序的數組是
A[0]……A[N-1]
,首先任意選取一個資料(通常選用數組的第一個數)作
為基準資料
,然後
将所有比它小的數都放到它左邊
,
所有比它大的數都放到它右邊
,
這個過程稱為一趟快速排序。
值得注意的是,然後我們就相當于将一個數組分成了兩截,這個時候我們可以繼續下去,對這兩個子數組繼續劃分,而實作這個,可以用遞歸。
我們将大的原始數組分成小的兩段,再繼續分,1分2,2分4...,展現了分而治之遞的思想,而實作上我們利用了遞歸!
一趟快速排序的算法是:
1)設定兩個變量i、j
(i,j我們可以看成是兩個哨兵,i是從左到右放哨,j是從右到左放哨)
排序開始的時候:i=0,j=N-1;
2)
每次都是将該數組第一個元素作為基準資料,指派給base
,即base=A[0];
3)從j(
哨兵j先走
)開始放哨,即由後開始向前搜尋(
j--
),找到第一個小于base的值
A[j]
,
每找到一個小于base的值,我們就檢視在i<j的條件下(哨兵i開始前進)是否存在比base值大的數A[i]
- 存在就進行交換
swap(A[i],A[j]
回跳到哨兵j繼續走
- 不存在,哨兵i就會繼續放哨,直到
i=j
最後
我們把這個過程遞歸即可,需要注意的就是分而治之時的基準值都是每一子數組的第一個元素
。(如圖,基準為6,第一個元素)
。。。。。
2)代碼實作
這是我自己看一半的原理,然後自己寫的:
public void quickSort(int[]array,int begin,int end){
if(begin>=0&&end>=0&&begin<end){//遞歸結束條件
int i=begin,j=end;
//以第一個為基準值
int base = array[begin];
while(i<j)//哨兵j先移動
{
if(array[j]<base)//哨兵j每找到一個小于基準值的
for(;i<j;i++){
if(array[i]>base){//哨兵i就找一次大于基準值的進行交換,交換一次就回去繼續下一輪交換
swap(array,i,j);
break;
}
//找不到比基準大的哨兵i繼續往右移動。
}
if(i==j)//因為現在i不清楚是從哪裡出來的我們需要判斷是break出來還是i==j
break;
j--;//否則我們哨兵j繼續搜尋
}
swap(array,begin,j);//交換基準值,實作小于基準值的都在左邊,大于基準值的都在右邊
//遞歸
quickSort(array,0,j-1);//左子數組
quickSort(array,j+1,end);//右子數組
}
}
書本的标準寫法:
public static int[] qsort(int arr[],int start,int end) {
int pivot = arr[start];
int i = start;
int j = end;
while (i<j) {
while ((i<j)&&(arr[j]>pivot)) {
j--;
}
while ((i<j)&&(arr[i]<pivot)) {
i++;
}
if ((arr[i]==arr[j])&&(i<j)) {
i++;
} else {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
if (i-1>start) arr=qsort(arr,start,i-1);
if (j+1<end) arr=qsort(arr,j+1,end);
return (arr);
}
3)Demo示範
我的:
public static void main(String[]args){
int[] array = new int[]{1,2,5,5,6,6,0,0,1,2,5,55,555,7777};
for(int arr:array){
System.out.print(arr+" ");
}
System.out.println();
new QuickSort().quickSort(array);
for(int arr:array){
System.out.print(arr+" ");
}
4)評價
從上面的結果就能知道快速排序是不穩定的,原因也很容易想,這裡就不贅述。快速排序的一次劃分算法從兩頭交替搜尋,直到i和j重合,是以
其時間複雜度是O(n);而整個快速排序算法的時間複雜度與劃分的趟數有關。
理想的情況是,每次劃分所選擇的中間數恰好将目前序列幾乎等分,經過
log2n
趟劃分,便可得到長度為1的子表。這樣,整個算法的時間複雜度為O(nlog2n)。
最壞的情況是,每次所選的中間數是目前序列中的最大或最小元素,這使得每次劃分所得的子表中一個為空表,另一子表的長度為原表的長度-1。這樣,長度為n的資料表的快速排序需要經過n趟劃分,使得整個排序算法的時間複雜度為O(n2)。
可以證明快速排序的平均時間複雜度也是O(nlog2n)。
是以,
該排序方法被認為是目前最好的一種内部排序方法。
從空間性能上看,盡管快速排序隻需要一個元素的輔助空間,但快速排序需要一個棧空間來實作遞歸。最好的情況下,即快速排序的每一趟排序都将元素序列均勻地分割成長度相近的兩個子表,所需棧的最大深度為log2(n+1);但最壞的情況下,棧的最大深度為n。這樣,快速排序的空間複雜度為
O(log2n))
。
3.3 最簡單直接的排序——直接選擇排序(挑最大/最小的那個)
1)原理
它的工作原理是:第一次從
待排序的n個資料元素中選出最小(或最大)的一個元素
,存放在序列的起始位置,然後
再從剩餘的n-1個未排序元素中尋找到最小(大)元素,然後放到目前的序列的起始位置。
以此類推,直到全部待排序的資料元素的個數為零。趟數是n-1趟。是不是很簡單啊?
我們每次都隻用找最小的一個數,然後把它從左到右依次放就好了。
2)代碼實作
public static void selectSort(int[]array){
for(int i=0;i<array.length;i++){
int min= i;//假定目前的序列第一個數就是最小的值
for(int j=i+1;j<array.length;j++){
if(array[j]<array[min])
min = j;//每次我們從剩下的數裡邊找最小值,記錄它的下标
}
//然後交換
if(i!=min)//如果最小值不是它自己我們才進行交換了。
swap(array,i,min);
}
}
3)Demo示範
public static void main(String[]args){
int[]array = {45,12,65,89,66,99,32,564,78};
for(int arr:array){
System.out.print(arr+" ");
}
System.out.println();
SelectSort.selectSort(array);
for(int arr:array){
System.out.print(arr+" ");
}
}
運作結果:
4)評價
首先我們肯定能夠知道
選擇排序是不穩定的排序方法。
它的比較次數與資料初始排序狀态無關,
第i趟比較的次數是 n-i
;
移動的次數與初始的排列有關,如果本來就排序好了,移動0次,反之最大移動了3*(n-1)次(我們交換一次要三步,總次數n-1)
。,
總的比較次數N=(n-1)+(n-2)+...+1=n*(n-1)/2。
時間複雜度O(n^2),空間複雜度明顯常數階O(1)
交換次數比冒泡排序少多了,由于交換所需CPU時間比比較所需的CPU時間多
,n值較小時,選擇排序比冒泡排序快。
但是因為
每次都要選擇最大的值交換,查找最大值浪費了好多時間。
3.4 看起來好煩的排序——堆排序(間接選擇排序、完全二叉樹)
1)原理
很口語的說法:
你有一個神器,每次都能一下子找到目前數組序列裡面的最小值所在(或者最大值所在,隻能其一)
那這個時候我們
進行直接選擇排序的時候
,
我們就能節省了找最值的時間了。直接交換到目前序列第一個元素就行了
。然後,在
剩下的數組序列
裡邊我們再用
神器
找到最小值所在,我們就交換,重複,直到排完數組的數。
那麼這個神器是什麼呢?那就是——堆,用數組實作的一個有特别屬性的完全二叉樹,戳我一下詳細了解堆的結構
堆分為兩種
- 最大堆,雙親結點的值比每一個孩子結點的值都要大。根結點值最大
- 最小堆,雙親結點的值比每一個孩子結點的值都要小。根結點值最小
注意:堆的根結點中存放的是最大或者最小元素,但是其他結點的排序順序是未知的。例如,在一個最大堆中,最大的那一個元素總是位于根結點 的位置,但是最小的元素則未必是最後一個元素。唯一能夠保證的是最小的元素是一個葉結點,但是不确定是哪一個。
數組實作的堆(完全二叉樹)圖示:
可以和層序周遊聯想一下就能清楚裡面的index的規律。
基于上面的一些介紹,我們可以知道算法的步驟應該是:
- 1)把輸入的數組建立堆的結構,可以神器般速度擷取(根結點)最大值(最小值)的所在
- 2)使用直接選擇排序将目前的堆擷取的最大值(最小值)與目前序列的末尾元素進行交換
- 3)此時我們破壞了堆原有的屬性,我們要把剩下的數組序列進行重建立立堆
- 4)回彈第二步,直到所有的數都排好序
是以難點就在于
怎麼建立堆,重建立立堆!
2)代碼實作
public static void heapSort(int[]array){
//1.對傳入的數組進行建立堆,這裡預設建立最小堆
heapSort(array,true);
}
public static void heapSort(int[]array,boolean minheap){
for(int i=array.length/2-1;i>=0;i--){
//建立最小最大堆,預設最小堆,即minheap=true
sift(array,i,array.length-1,minheap);
}
//排序,使用直接選擇排序
for(int j=array.length-1;j>0;j--){
//現在的數組第一個就是根結點,最小值所在,進行交換,把它放到最右邊
swap(array,0,j);
//重建立立堆
sift(array,0,j-1,minheap);//将剩下的j-1個數,把它們調整為堆, 實質上是自上而下,自左向右進行調整的
}
//建立堆的方法
/**
* 私有方法,隻允許被堆排序調用
* @param array 要排序數組
* @param parent 雙親結點
* @param end 數組長度
* @param minheap 是否建立最小堆
*/
private static void sift(int[]array,int parent,int end,boolean minheap){
int child = 2*parent+1;//利用公式,建立child是parent的左孩子,+1則是右孩子
int value = array[parent];//擷取目前雙親結點值
for(;child<end;child=child*2+1){//周遊
//注意這裡的child必須小于end,防止越界,建立最小堆,右孩子如果比左孩子小,我們就将現在的孩子換到右孩子
//因為現在如果右孩子大于雙親,自然左孩子也大于雙親
if(child<end&&(minheap?array[child]>array[child+1]:array[child]<array[child+1]))//比較左孩子與右孩子的大小
child++;//右孩子如果比左孩子大,我們就将現在的孩子換到右孩子
//判斷是否符合最小堆的特性, 如果右孩子大于雙親,自然左孩子也大于雙親,符合
if(minheap?value>array[child]:value<array[child]){
swap(array,parent,child);右孩子沒有大于雙親,我們将其交換
parent = child;//然後我們更新雙親結點和孩子結點
}
//如果不是,說明已經符合我們的要求了。
else
break;
}
}
3)Demo
4)評價
堆排序是利用堆這種資料結構而設計的一種排序算法,堆排序是一種選擇排序,整體主要由
建構初始堆
+
交換堆頂元素和數組末尾元素并重建堆
這
兩部分組成
。其中建構初始堆經推導複雜度為O(n),在交換并重建堆的過程中,需交換n-1次,而重建堆的過程中,根據完全二叉樹的性質,[log2(n-1),log2(n-2)…1]逐漸遞減,近似為nlogn。
是以堆排序時間複雜度一般認為就是O(nlogn)級。
5)應用
不僅用于排序算法,還可以應用于頻繁選擇極值的問題,如優先隊列,、Huffman、Prim、Kruskal、Dijkstra、Floyd等算法。
3.5 分治法的典型應用——歸并排序(分治遞歸)
1)原理
非常棒的歸并排序講解,圖解
歸并排序(英語:Merge sort,或mergesort),是建立在歸并操作上的一種有效的排序算法,效率為 O(nlog n)}(大O符号)。1945年由約翰·馮·諾伊曼首次提出。該算法是采用分治法(Divide and Conquer)的一個非常典型的應用,且各層分治遞歸可以同時進行。
原理描述:
遞歸回彈的過程真爽!
圖示:
分:
我們
遞歸序列進行對半分(奇數則相差1),繼續遞歸進行對半分,直到無法再分
治:然後遞歸回彈!開始
對這些子序列進行排序及合并操作
,兩個小小序列合并成小序列,兩個小序列合并成大序列,然後就排序好了。
作為一種典型的分而治之思想的算法應用,歸并排序的實作分為兩種方法:
- 自上而下的遞歸;
- 自下而上的疊代;
2)代碼實作
個人比較喜歡遞歸實作:
public static void mergeSort(int []arr){
int []temp = new int[arr.length];//在排序前,先建好一個長度等于原數組長度的臨時數組,避免遞歸中頻繁開辟空間
mergeSort(arr,0,arr.length-1,temp);
}
/**
*
* @param arr 傳入數組
* @param left 目前子數組的起始下标
* @param right 目前子數組的結束下标
* @param temp 拷貝暫存數組
*/
private static void mergeSort(int[] arr,int left,int right,int []temp){
if(left<right){//這裡是遞歸結束的條件,我們是對半分,那當left==right的時候肯定大家都是隻有一個元素了。
int mid = (left+right)/2;//對半分,比如總長度是10,left=0,right=9,mid=4确實是中間分了,0~4,5~9
//當長度9,left=0,right=8,mid=4,0~4,5~8
mergeSort(arr,left,mid,temp);//左邊歸并排序,使得左子序列有序
mergeSort(arr,mid+1,right,temp);//右邊歸并排序,使得右子序列有序
merge(arr,left,mid,right,temp);//将兩個有序子數組合并操作
}
}
private static void merge(int[] arr,int left,int mid,int right,int[] temp){
int i = left;//左序列起始下标
int j = mid+1;//右序列起始下标
int t = 0;//臨時數組指針
while (i<=mid && j<=right){
if(arr[i]<=arr[j]){//比較兩個序列第一個元素誰小,誰小先拷貝誰到temp,然後對應子序列下标加1
temp[t++] = arr[i++];
}else {
temp[t++] = arr[j++];
}
}
while(i<=mid){//将左邊剩餘元素填充進temp中——左序列有一些數總是比右邊的大的數
temp[t++] = arr[i++];
}
while(j<=right){//将右序列剩餘元素填充進temp中——右序列有一些數總是比左邊的大的數
temp[t++] = arr[j++];
}
t = 0;
//将temp中的元素全部拷貝到原數組中
while(left <= right){//注意這裡的條件是left——right
arr[left++] = temp[t++];
}
}
當然也得學會疊代法實作:
public static void mergeSort(int[] arr) {
int[] orderedArr = new int[arr.length];//建立一個數組用于臨時拷貝
for (int i = 2; i < arr.length * 2; i *= 2) {//逆向看,一個數組被拆分到最後有幾塊,對應子序列起始下标末尾下标的規律是什麼
for (int j = 0; j < (arr.length + i - 1) / i; j++) {
int left = i * j;//規律所在
int mid = left + i / 2 >= arr.length ? (arr.length - 1) : (left + i / 2);
int right = i * (j + 1) - 1 >= arr.length ? (arr.length - 1) : (i * (j + 1) - 1);
int start = left, l = left, m = mid;
while (l < mid && m <= right) {
if (arr[l] < arr[m]) {
orderedArr[start++] = arr[l++];
} else {
orderedArr[start++] = arr[m++];
}
}
while (l < mid)
orderedArr[start++] = arr[l++];
while (m <= right)
orderedArr[start++] = arr[m++];
System.arraycopy(orderedArr, left, arr, left, right - left + 1);//拷貝
}
}
}
3)Demo
4)評價
歸并排序嚴格遵循從左到右或從右到左的順序合并子資料序列, 它不會改變相同資料之間的相對順序, 是以歸并排序是一種
穩定的排序算法
.分階段可以了解為就是遞歸拆分子序列的過程,遞歸深度為log2n,比較操作的次數介于
(nlog n)/2
和
nlog n-n+1
。 指派操作的次數是
2nlog n
。歸并算法的空間複雜度為:
O(n)
3.6 跟打牌一樣的排序——插入算法(每個數都找到它應該插入的位置)
1)原理
以第一個數為起始子序列
,從
第二個數
開始,将
這個數與與子序列比較
,
找到自己應該插入的位置
,找到了,就
插入
進去,
起始子序列變為從第一個數到第二個數
(
在這之前需要數組騰出空間
給它插入)。完成一個數的插入,繼續下一個數。直到最後一個數插入完畢。
簡單得跟我們打牌整理牌一樣。
2)代碼實作
//從右邊第二個數字開始,在與前面的子序列進行比較,找到屬于自己的位置進行插入
public static void straghtInsertSort(int []array){
//
straghtInsertSort(array,true);//預設進行升序
}
public static void straghtInsertSort(int []array,boolean flag){
if(flag){//選擇是升序還是降序排序
for(int i=1;i<array.length;i++){//從第二個數開始
int temp = array[i],j;
for( j=i-1;j>=0&&temp<array[j];j--)//array[i]是要插入的數
//即從j到i-1這些數都需要往後面移動一位,空出的位置給array[i]插入,
array[j+1] = array[j];//每比較一次我們就知道這個數需要往後面諾出一個位置了。
array[j+1] = temp ;//注意這裡要加1
System.out.println("插入位置是"+i+",插入的數字是"+temp);
}
}
else{//代碼基本一緻
for(int i=1;i<array.length;i++){//從第二個數開始,預設第一個數是最小的
int temp = array[i],j;
for( j=i-1;j>=0&&temp>array[j];j--)//array[i]是要插入的數
//即從j到i-1這些數都需要往後面移動一位,空出的位置給array[i]插入,
array[j+1] = array[j];//每比較一次我們就知道這個數需要往後面諾出一個位置了。
array[j+1] = temp ;//注意這裡要加1
System.out.println("插入位置是"+i+",插入的數字是"+temp);
}
}
}
3)Demo
4)優化
我們在查找該數的插入位置是用順序查找,但是因為與該數比較的序列它是有序的啊,那不就可以用二分查找的辦法了?這就是——二分法插入排序
代碼:
public static void straghtInsertSort1(int []array){//優化
for(int i=1;i<array.length;i++){//從第二個數開始,預設第一個數是最小的
int temp = array[i],start=0,end=i-1,mid=-1;
for( ;end>=start;)//array[i]是要插入的數
{
mid = start+(end-start)/2;
if(array[mid]>temp)
end=mid-1;
else //元素相同時,我們也插入後面,肯能破壞穩定性
start=mid+1;
}
//移動元素
for(int len=i-1;len>=start;len--){
array[len+1] = array[len];
}
array[start]=temp;
System.out.println("插入位置是"+start+",插入的數字是"+temp);
}
}
5)展示
原算法未優化時
使用二分法插入優化時:
。。資料比較少,沒展現出來。。。。
6)評價
跟打牌一樣的算法,算法是穩定的。時間複雜度平均時間O(n^2),空間複雜度O(1)
3.7 改進直接插入排序的排序——希爾排序(縮小增量排序,Δ牛筆)
1)原理
很簡單,一張圖就能看懂
希爾排序是基于插入排序的以下兩點性質而提出改進方法的:
- 插入排序在對幾乎已經排好序的資料操作時,效率高,即可以達到線性排序的效率。
- 但插入排序一般來說是低效的,因為插入排序每次隻能将資料移動一位。
該方法實質上是一種分組插入方法
比較相隔較遠距離(稱為增量)的數,使得數移動時能跨過多個元素,則進行一次比較就可能消除多個元素交換。D.L.shell于1959年在以他名字命名的排序算法中實作了這一思想。算法先将要排序的一組數按
某個增量d分成若幹組
,每組中記錄的
下标相差d
.
對每組中全部元素進行排序
,然後再用一個較小的增量對它進行,在每組中再進行排序。當增量減到1時,整個要排序的數被分成一組,排序完成。
一般的初次取序列的一半為增量,以後每次減半,直到增量為1。
2)代碼實作
public static void shellSort(int[]array){
for(int delta=array.length/2;delta>0;delta=delta/=2){//控制增量的變化
for(int i=delta;i<array.length;i++){//周遊每個組
int temp = array[i],j;
//組内排序
for(j=i-delta;j>=0&&temp<=array[j];j-=delta){
array[j+delta]=array[j];
}
array[j+delta] = temp;
}
}
}
3)Demo
???????????????????????????
5)評價
希爾排序是非穩定排序算法。不需要大量的輔助空間,和歸并排序一樣容易實作。希爾排序是基于插入排序的一種算法, 在此算法基礎之上增加了一個新的特性,提高了效率。
希爾排序的時間的時間複雜度為O( n^1.5))
,希爾排序時間
複雜度的下界是n*log2n
。希爾排序
沒有快速排序算法快 O(n(logn))
,是以
中等大小規模表現良好,對規模非常大的資料排序不是最優選擇
。但是
比O( n^2)複雜度的算法快得多
。并且希爾排序非常容易實作,算法代碼短而簡單。 此外,希爾算法在最壞的情況下和平均情況下執行效率相差不是很多,與此同時快速排序在最壞的情況下執行的效率會非常差。
專家們提倡,幾乎任何排序工作在開始時都可以用希爾排序,若在實際使用中證明它不夠快,再改成快速排序這樣更進階的排序算法.
本質上講,希爾排序算法是直接插入排序算法的一種改進,減少了其複制的次數,速度要快很多。 Good?
3.8 傳說中時間複雜度為O(n)的排序——計數排序(非比較穩定排序)
1)原理
計數排序(Counting sort)是一種
穩定的線性時間排序算法
。該算法于1954年由 Harold H. Seward 提出。計數排序使用一個額外的數組用來計數。
簡單巧妙的原理,假設有數組A[10]值為:
1~10個數
,現在我們
統計出現的每一個數的個數,如出現5一次我們記一次,假設出現了3次
,我們就把
3存進一個數組計數器相應的位置
,這個數組計數器相應的下标都加上或者減去一個定值(delta)能夠讓我們知道存進來的是數組A中的哪個數(看作映射),而這個計數器下标裡邊的數代表該數出現的次數。
這樣我們就知道一個數出現的次數是多少了。我們利用了映射——找到最大最小值
max,min
,建立數組計數器
count
的長度
max-min+1
,那我們令delta為0+min;那count[0]存放的是(0+delta)的值出現的個數,即min的個數!
排序過程:就是把計數器裡的數一個一個地放回去。
是以就分兩步:
- 計數
- 放回排序
圖解
2)代碼實作
public static void countSort(int[]array){
//找到最大最小值,建立基于這個長度(max-min+1)的一個數組容器來計數,我們可以建立一個下标與存儲的數組的0值的映射
int delta,min=array[0],max=array[0];
//1.找最大最小值
for(int i=1;i<array.length;i++){
if(array[i]<min)
min=array[i];//找最小值
if(array[i]>max)
max=array[i];//找最大值
}
//建立一個用于計數的數組,對應的下标映射實際數組的值
delta = 0+min;//映射關系就是計數的數組下标與實際的值相差delta
int []count_map = new int[max-min+1]; //count_map裡的值都初始化為0;
//開始計數
for(int i=0;i<array.length;i++)
//實作計數,array[i]-delta表示array[i]在count_map的數組下标映射,同一個下标則表示相同的數,該數大小為i+delta,++則實作計數
count_map[array[i]-delta]++;
//計算完數組以後,我們開始依次放回,預設升序
int i=0;//用來訓示計數數組的下标是否需要移動,當對應的count_map[i]==0,i++
for(int j=0;j<array.length;){//填充,j用來控制array下标
if(count_map[i]>0){
array[j] =i+delta;//放回一個數
j++;
count_map[i]--;//計數器減1;
}
else i++;//放完了,就進行放下一個不重複的數
}
}
3)Demo
還是上次選擇排序的那個數組,我這裡使用了降序:
int []array1 = {12,121,5,45,4,4,74,978,979,7,4,6,64,6,4554,979,44,55,1,215,46,22,6464,7977,797,797,79,9,11};
long t1 = System.currentTimeMillis();
for(int i=0;i<100;i++)
countSort(array1);
//countSort(array1,false);
System.out.println((System.currentTimeMillis()-t1)+"ms");
4)評價
當輸入的元素是n 個0到k之間的整數時,它的運作時間是 O(n + k)。計數排序不是比較排序,排序的速度快于任何比較排序算法。由于用來計數的數組的長度取決于待排序數組中資料的範圍(等于待排序數組的最大值與最小值的差加上1),這使得計數排序對于資料範圍很大的數組,需要大量時間和記憶體。值得一提它是
穩定
的排序。
最佳情況:T(n) = O(n+k) 最差情況:T(n) = O(n+k) 平均情況:T(n) = O(n+k)
3.9 快快快的桶裝資料排序——桶排序(利用了快排的特性和計數裡的類似映射)
1)原理
桶排序是計數排序的更新版。桶排序 (Bucket sort)的工作的原理:假設輸入資料服從均勻分布,将資料分到有限數量的桶裡,每個桶再分别排序(有可能再使用别的排序算法或是以遞歸方式繼續使用桶排序進行排
讓我想一下怎麼用口水話說:
- 1)我們收到一個數組,我們就
以某種規則指定了桶的個數n
每個飯桶有它自己的飯桶号碼,從0到n-1(嘻嘻)
- 2) 現在我們開始将數組裡的數放進桶裡了,放進哪個編号的桶呢?規則就是找到最大值,最小值max,min,
進而制定了每個飯桶它的“飯量範圍”
飯量範圍
把數放進自己對應的飯桶!
-
一點就懂的經典十大排序算法1、概述2、十大算法性能比較3、排序算法精講4、總結 - 3)現在就是
将每個飯桶内部的數進行排序
- 4)将
内部排好序的桶按照飯量大小進行合并
一個很棒的視訊講解——點我快速了解桶排序
2)代碼實作
我自己寫的使用二維數組實作的:(有點麻煩,因為二維數組在插入數的時候,如果同時進行排序,要移動很多數)這裡設定桶數10。當然我們也可以使用函數映射生成桶的個數
public static void bucketSort(int[] array)//data為待排序數組
{
int n = array.length, max = array[0], min = array[0];
int[][] bask = new int[10][n];//定義10個桶來放資料,桶的索引為0到9,每個桶的數量最多存放n個數,
//1、找最大值最小值制定桶的飯量
for (int i = 1; i < array.length; i++) {
if (min > array[i])
min = array[i];
if (max < array[i])
max = array[i];
}
int delta = (max - min ) / 10+1;//注意這裡要加1,不然num會越界
//定義一個數組來記錄對應的桶現在吃了多少個數
int[] len_bask = new int[n];//預設值為0
//2、開始将數放進桶裡
for (int i = 0; i < n; i++) {//周遊原數組
int num = (array[i] - min) / delta;//每一個數對應的桶号
// 放進對應桶号的對應位置
bask[num][len_bask[num]] = array[i];
//桶内數的個數加1
len_bask[num]++;
}
//3、各個桶分别排序,這裡使用計數排序
for (int i = 0; i < 10; i++) {//周遊桶,進行排序
//因為我們使用二維數組實作,目前每個桶存放的數值個數為len_bask[i]
if(len_bask[i]!=0)//對非空的桶排序
countSort(bask[i], len_bask[i]);
}
//4、合并桶喽
int k=0;
for(int i=0;i<10;i++){//周遊桶,進行合并
for(int j=0;j<len_bask[i];j++){
array[k++]=bask[i][j];
}
}
}
3)Demo
還是上次的計數排序的原數組
我把列印資訊去掉以後,隻用了
1ms
,而計數排序(3.8的計數排序用了
9ms
)
4)評價
桶排序最好情況下使用線性時間O(n),桶排序的時間複雜度,取決與對各個桶之間資料進行排序的時間複雜度,因為其它部分的時間複雜度都為O(n)。很顯然,桶劃分的越小,各個桶之間的資料越少,排序所用的時間也會越少。但相應的空間消耗就會增大。
平均時間複雜度為線性的O(N+C),其中C=N*(logN-logM)。如果相對于同樣的N,桶數量M越大,其效率越高,最好的時間複雜度達到O(N)(當N=M時)即極限情況下每個桶隻有一個資料時。桶排序的最好效率能夠達到O(N)。
當然桶排序的空間複雜度 為O(N+M),如果輸入資料非常龐大,而桶的數量也非常多,則空間代價無疑是昂貴的
。此外,
桶排序是穩定的。
5)應用
1.海量資料
一年的全國聯考考生人數為500 萬,分數使用标準分,最低100 ,最高900 ,沒有小數,要求對這500 萬元素的數組進行排序。
分析:對500W資料排序,如果基于比較的先進排序,平均比較次數為O(5000000log5000000)≈1.112億。但是我們發現,這些資料都有特殊的條件: 100=<score<=900。那麼我們就可以考慮桶排序這樣一個“投機取巧”的辦法、讓其在毫秒級别就完成500萬排序。
方法:建立801(900-100)個桶。将每個考生的分數丢進f(score)=score-100的桶中。這個過程從頭到尾周遊一遍資料隻需要500W次。然後根據桶号大小依次将桶中數值輸出,即可以得到一個有序的序列。而且可以很容易的得到100分有**人,501分有***人。
2.大檔案的資料排序
在一個檔案中有10G個整數,亂序排列,要求找出中位數。記憶體限制為2G。隻寫出思路即可(記憶體限制為2G意思是可以使用2G空間來運作程式,而不考慮本機上其他軟體記憶體占用情況。) 關于中位數:資料排序後,位置在最中間的數值。即将資料分成兩部分,一部分大于該數值,一部分小于該數值。中位數的位置:當樣本數為奇數時,中位數=(N+1)/2 ; 當樣本數為偶數時,中位數為N/2與1+N/2的均值(那麼10G個數的中位數,就第5G大的數與第5G+1大的數的均值了)。
分析:既然要找中位數,很簡單就是排序的想法。那麼基于位元組的桶排序是一個可行的方法。
思想:将整型的每1byte作為一個關鍵字,也就是說一個整形可以拆成4個keys,而且最高位的keys越大,整數越大。如果高位keys相同,則比較次高位的keys。整個比較過程類似于字元串的字典序。
參考資料:百度百科桶排序的應用
3.10 每次都看位數值的排序——基數排序(利用了桶,基數對應進制)
1)原理
以LSD實作為例:(從最低位開始進桶的基數排序)
如下圖,最低位數相同的都進入相應下标的桶,如第一次,最低位是3的全進了3号桶,最低位是9的全進了9号桶。因為正整數的最低位隻能是0~9,是以我們使用數組bask的長度為10,相應的下标為對應的位數的值,全部數組都進桶了完成一次對目前最低位的周遊,然後将桶按照編号合并(跟桶排序的最後一步相同),我們開始進行下一個位的進桶,比如十位是1的全進1号桶,我們這個時候不去理個位了。重複直到周遊完最大的數的最高位。最後得到的數組就排好序了。這就是10進制的LSD基數排序原理
實際例子:
假設原來有一串數值如下所示:
73, 22, 93, 43, 55, 14, 28, 65, 39, 81
1)首先根據
個位數的數值
,在走訪數值時将它們配置設定至編号0到9的桶子中:
1 81
2 22
3 73 93 43
4 14
5 55 65
6
7
8 28
9 39
2)接下來将
這些桶子中的數值重新串接起來
,成為以下的數列:
81, 22, 73, 93, 43, 14, 55, 65, 28, 39
接着再進行一次配置設定,這次是
根據十位數來配置設定
:
1 14
2 22 28
3 39
4 43
5 55
6 65
7 73
8 81
9 93
3)接下來将這些桶子中的數值重新串接起來,成為以下的數列:
14, 22, 28, 39, 43, 55, 65, 73, 81, 93
這時候整個數列已經排序完畢;如果排序的對象有三位數以上,則
持續進行以上的動作直至最高位數為止。
LSD的基數排序适用于位數小的數列,如果位數多的話,使用MSD的效率會比較好。MSD的方式與LSD相反,是由高位數為基底開始進行配置設定,但在配置設定之後并不馬上合并回一個數組中,而是在每個“桶子”中建立“子桶”,将每個桶子中的數值按照下一數位的值配置設定到“子桶”中。在進行完最低位數的配置設定後再合并回單一的數組中。
2)代碼實作
這裡示範全是正整數的排序:
public static void radixSort(int[]array){
int n=1;//表示從個位開始
int max=array[0];//最大的數預設a【0】
int [][]baske=new int[10][array.length];//因為位數隻能是0~9,是以我們建立了10個桶,每個桶最多容納array.length個數
//我們又是用二維數組表示桶,則一樣需要一個數組來記錄該桶裡面存了多少個數
int []len_bask = new int[array.length];
for(int i=0;i<array.length;i++){
len_bask[i]=0;//初始化為0
if(max<array[i])
max = array[i];
}
int k=0;//用來控制array數組指派下标
//找到該數組裡最大是數有幾位
while(max!=0){
for (int value : array) {
//取最低位的數值出來
int lsd = (value / n) % 10;
baske[lsd][len_bask[lsd]] = value;//位數相同的進同一個桶,
len_bask[lsd]++; // 同時桶内數的個數加1
}
//現在将桶内的數取出來合并
for(int i=0;i<10;i++){//外圍控制桶的下标
if(len_bask[i]!=0)//桶不空
{
for(int j=0;j<len_bask[i];j++){//控制桶内
array[k]=baske[i][j];
k++;
}
len_bask[i]=0;//周遊完該桶内的數,桶内的數就沒有了。
}
}
//繼續進行下一個位
k=0;
n *=10;
max/=10;//,同時我們讓最大值位數降1,假設剛才是max=9,我們就隻需要比較一個位數了。
}
}
3)Demo
還是上次的那個數組:
4)評價
标準的基數排序每次從小到大排序十進制下的一個位,并且隻關心這一個位,也可以進行設計二進制的基數排序。
不知道細心的夥伴發現沒有,上面的算法我們隻能進行正整數的排序。那
假設有負整數和正整數呢?我們可以加桶的個數,比如0~9的桶裝正整數,10到19的桶裝負整數
;那如果不是整數呢?感謝
IEEE 754的标準
,它制定的浮點标準還帶有一個特性:如果不考慮符号位(浮點數是按照類似于原碼使用一個bit表示符号位s,s = 1表示負數),那麼同符号浮點數的比較可以等價于無符号整數的比較,方法就是先做一次基數排序,然後再調整正負數部分順序即可。是以現在已經可以實作浮點數的基數排序了!!!點我檢視基數排序之浮點數排序
最佳情況:T(n) = O(n * k) 最差情況:T(n) = O(n * k) 平均情況:T(n) = O(n * k)
基數排序有兩種方法:
- MSD 從高位開始進行排序
- LSD 從低位開始進行排序
5)基數排序 vs 計數排序 vs 桶排序
這三種排序算法都利用了桶的概念,但對桶的使用方法上有明顯差異:
- 基數排序:根據鍵值的每位數字來配置設定桶(根據位數)
- 計數排序:每個桶隻存儲單一鍵值(下标映射實際的數)
- 桶排序:每個桶存儲一定範圍的數值(根據一個函數映射得到一個桶容納數的範圍)
4、總結
借一張圖來總結吧:
以上是一邊學一邊總結的,如果有錯誤,請大佬們給小弟指出。