回歸分析的定義:回歸分析是确定兩種或兩種以上變量間互相依賴的定量關系的一種統計分析方法。運用十分廣泛。其表達形式為y = w'x+e,e為誤差服從均值為0的正态分布。回歸分析中,隻包括一個自變量和一個因變量,且二者的關系可用一條直線近似表示,這種回歸分析稱為一進制線性回歸分析。如果回歸分析中包括兩個或兩個以上的自變量,且因變量和自變量之間是線性關系,則稱為多元線性回歸分析。
多元線性回歸在醫學上有着廣泛的應用
1:影響因素分析,大多數疾病都有多種緻病原因,疾病的預後也是由多種因素決定的。
2:估計與預測。
3:統計控制,給定應變量y指定一個确定值或在一定範圍内波動,通過控制自變量的值來實作。
多元線性回歸分析的資料結構
| 實驗對象 | Y(因變量) | X1(自變量) | X2 | …… | Xm |
| 1 | Y1 | X11 | X12 | …… | X1m |
| 2 | Y2 | X21 | X22 | …… | X2m |
| 3 | …… | …… | …… | …… | …… |
| 4 | yn | Xn1 | Xn2 | …… | Xnm |
其中y取值服從正态分布
多元線性回歸分析方程:
y=b0+b1x1+b2x2+……+bmxm+e
其中b0為截距,b1,b2……為偏回歸系數,e表示去除m個自變量對y的影響後的随機誤差,也稱為殘差。bi表示當其他p-1個變量的作用加以固定後,xi改變一個機關,y改變bi個機關。多元線性回歸模型要滿足以下條件:
1:y與x之間有線性關系
2:各觀測值y之間互相獨立
3:殘差e服從均數為0,方差為σ2的正态分布,即對任意一組自變量x值,應變量y具有相同的方差,并服從正态分布。
例子:27名糖尿病患者的血清總膽固醇、甘油三酯、空腹胰島素、糖化血紅蛋白、空腹血糖測量值如下表,建立血糖與其他幾個名額的多元線性回歸方程。
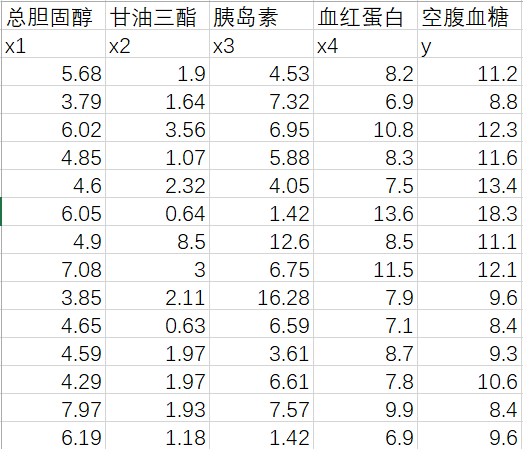
stata指令:regress y x1 x2 x3x4
結果:
F值=8.28,p值=0.0003,說明該回歸方程具有統計學意義。與空腹血糖有相關意義的名額為x3,x4(p<0.05).胰島素和糖化血紅蛋白。