Mayor’s posters(線段樹+離散化)
Time limit:1000 ms
Memory limit:65536 kB
OS:Linux
judge:https://vjudge.net/contest/295911#problem/D
描述
The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules:
Every candidate can place exactly one poster on the wall.
All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown).
The wall is divided into segments and the width of each segment is one byte.
Each poster must completely cover a contiguous number of wall segments.
They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections.
Your task is to find the number of visible posters when all the posters are placed given the information about posters’ size, their place and order of placement on the electoral wall.
Input
The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l i, l i+1 ,… , ri.
Output
For each input data set print the number of visible posters after all the posters are placed.
The picture below illustrates the case of the sample input.
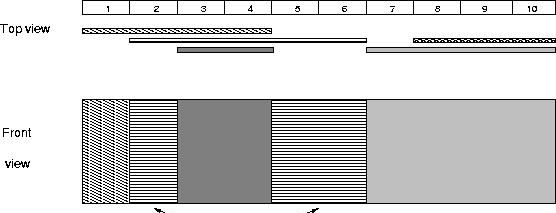
Sample Input
1
5
1 4
2 6
8 10
3 4
7 10
Sample Output
4
題意
AB州拜托鎮的公民無法忍受市長選舉競選中的候選人随心所欲地在各個地方張貼他們的選舉海報。市議會最終決定修建一道選舉牆,用于張貼海報,并引入以下規則:
每個候選人都可以在牆上貼一張海報。
所有海報的高度相同,等于牆的高度;海報的寬度可以是任意整數位元組(位元組是長度的機關,以位元組為機關)。
牆被分成段,每個段的寬度為一個位元組。
每幅海報必須完全覆寫相鄰數量的牆段。
他們已經建造了一堵10000000位元組長的牆(這樣就有足夠的地方容納所有候選人)。競選活動重新開始時,候選人把海報貼在牆上,海報的寬度差别很大。此外,候選人開始把他們的海報放在已經被其他海報占據的牆上。所有人都很好奇,在選舉前的最後一天,誰的海報會清晰可見(全部或部分)。
你的任務是找出所有海報放置時可見海報的數量,給出海報的尺寸、位置和在選舉牆上的放置順序。
輸入
輸入的第一行包含一個數字C,給出後面的事例數。單個案例的第一行資料包含數字1<=n<=10000。接下來的n行描述了海報的放置順序。n行中的i-th行包含兩個整數l i和ri,分别是i-th海報左端和右端所占的牆段數。我們知道,每1<=i<=n,1<=l i<=ri<=10000000。第i張海報貼好後,它完全覆寫了編号為l i、l i+1、…,RI。
産量
對于每個輸入資料集,在放置所有海報後列印可見海報的數量。
下圖說明了示例輸入的情況。
思路
一開始就想到了用線段樹,但牆的長度太大記憶體會超限,于是就想到了離散化:
把所有用到的節點存下來,存完排序,然後把這段序列建樹,就能大大縮減樹的大小。通俗來說就是如果按照牆的真實長度建樹,那麼其中有些節點是壓根用不到的,就像把1~3内的點變成0,那麼我們隻需要記錄下兩個端點1和3就可以了,2就是無用的
代碼
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <map>
#define maxn 100005
#define ll long long
#define _for(i, a) for(int i = 0; i < (a); i++)
#define _rep(i, a, b) for(int i = (a); i <= (b); i++)
using namespace std;
struct {
int l, r;
}tem[maxn];
int a[maxn * 4];
map<int, int> b;
int num[maxn * 2], tt = 0;
void upd(int node, int beg, int end, int l, int r, int val) {
if (a[node]) {
a[node * 2] = a[node];
a[node * 2 + 1] = a[node];
a[node] = 0;
}
if (beg == l && end == r) {
a[node] = val;
return;
}
int mid = (beg + end) / 2;
if (mid >= r) upd(node * 2, beg, mid, l, r, val);
else if (mid < l) upd(node * 2 + 1, mid + 1, end, l, r, val);
else {
upd(node * 2, beg, mid, l, mid, val);
upd(node * 2 + 1, mid + 1, end, mid + 1, r, val);
}
}
void query(int node, int beg, int end) {
if (a[node]) {
b[a[node]] += (end - beg + 1);
return;
}
if (beg == end) return;
int mid = (beg + end) / 2;
query(node * 2, beg, mid);
query(node * 2 + 1, mid + 1, end);
}
int main() {
//freopen("in.txt", "r", stdin);
int T;
scanf("%d", &T);
while (T--) {
memset(a, 0, sizeof(a));
b.clear();
int n;
scanf("%d", &n);
_for(i, n) {
scanf("%d%d", &tem[i].l, &tem[i].r);
num[tt++] = tem[i].l;
num[tt++] = tem[i].r;
}
sort(num, num + tt);
tt = unique(num, num + tt) - num;
_for(i, n) {
int l, r;
l = lower_bound(num, num + tt, tem[i].l) - num;
r = lower_bound(num, num + tt, tem[i].r) - num;
upd(1, 1, tt, l + 1, r + 1, i + 1);
}
query(1, 1, tt);
printf("%d\n", b.size());
}
return 0;
}