線性代數行列式方程求解(正交矩陣的行列式)

大家好，又見面了，我是你們的朋友全棧君。

C++代碼實作行列式求值

• 行列式求值的基本思路
• 思路一——行列式展開
  • 不利用輔助函數的遞歸：
  • 輔助函數遞歸
  • 奉上一個完整代碼，可以直接根據提示計算
• 思路二——逆序數全排列
• 思路三——初等變換
• 調試分析
• 實作線代其它操作的參考連結

線性代數行列式求值算的可真是讓人CPU疼，但計算機是不累的，是以用一個c++程式幫助你驗證求解行列式的值吧。

行列式求值的基本思路

行列式求值主要有以下這幾種思路：

1. 行列式等于它的任意列（或行）各個元素與其對應代數餘子式乘積的和。
2. 直接利用行列式的定義（逆序數）求解
3. 利用行列式的性質做初等變換在求解：

• 性質1：互換行列式的兩列（或兩行），行列式僅改變符号。
• 性質2：行列式某行（或某列）的 k 倍加到另一行（或列）上，行列式不變。

思路一——行列式展開

首先再次介紹下餘子式和代數餘子式：

• 餘子式：在 n 階行列式中，把某個元素所在的行列都去掉之後，剩下的 n-1 階行列式就叫做該元素的餘子式：

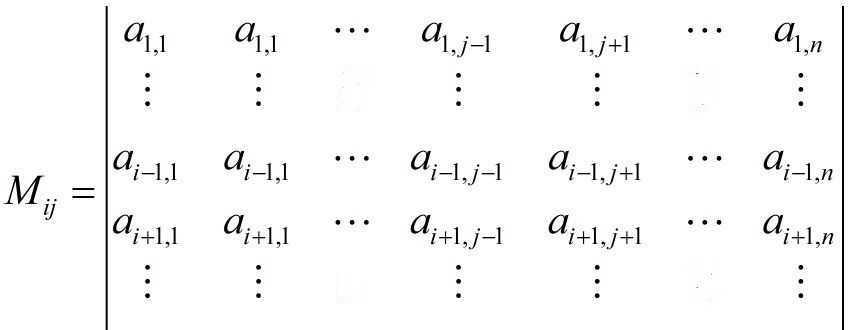
• 代數餘子式：

  餘子式再乘以-1的i+j次方（ij為行列式的行和列）

**我們可以看到行列式展開得到的代數餘子式又是一個行列式，這是一個逐漸求精的過程。顯然可以用遞歸的方法。

基本算法：

1. 行列式按第一行展開：
2. 循環求各個元素與其對應代數餘子式乘積的和。
3. 其中餘子式求值遞歸為行列式求值

4. 遞歸終止條件：

   行列式階數為1，傳回該數

下面給出兩種遞歸的方法：**

不利用輔助函數的遞歸：

代碼如下：

double cal(double **det,int n)//det-行列式，n:行列式的階數
{ 
   
	double detVal = 0;//行列式的值
	
	if(n == 1)//遞歸終止條件 
	return det[0][0]; 
	
	double **tempdet = new double *[n-1];//用來存儲餘相應的餘子式
	 for(int i=0;i<n-1;i++)
	  tempdet[i] = new double[n-1];
	for(int i=0;i<n;i++)//第一重循環，行列式按第一行展開 
	{ 
   
		for(int j=0;j<n-1;j++)
		for(int k=0;k<n-1;k++)
		{ 
   
			if(k <i)
			tempdet[j][k]=det[j+1][k] ;
			else
			tempdet[j][k]=det[j+1][k+1];
		}
		detVal += det[0][i] * pow(-1.0,i) * cal(tempdet,n-1);
	
	 } 
	 return detVal;
}            

複制

輔助函數遞歸

這一種建構了一個輔助函數，可以更加直覺的了解此遞歸算法

//獲得det[i][j]餘子式行列式 
vector<vector<double> > getComplementMinor(vector<vector<double> > det,int i,int j) ;
//獲得行列式det的值 
double getDetVal(vector<vector<double> > det);           

複制

//獲得det[i][j]餘子式行列式 
vector<vector<double> > getComplementMinor(vector<vector<double> > det,int i,int j) 
{ 
      
     
	int n=det.size(),m=det[0].size();//n為det的行，m為det的列；
	vector<vector<double> > ans(n-1);//儲存獲得的結果
	for(int k=0;k<n-1;k++)
	for(int l=0;l<n-1;l++)
	{ 
   
		ans[k].push_back(det[k<i?k:k+1][l<j?l:l+1]);
	}
	return ans;
}

double getDetVal(vector<vector<double> > det)
{ 
      
    double ans=0;
	int n=det.size(),m=det[0].size();//n為det的行，m為det的列；
	if(n != m)
    { 
   
    	 cout<<" 您輸入的矩陣不是方陣！求麼子行列式！";
    	 exit(1);
	} 
	if(det.size() == 1)
	return det[0][0];
	
	for(int i=0;i<m;i++)
	{ 
   
		ans+=det[0][i] * pow(-1,i)*getDetVal(getComplementMinor(det,0,i));
	}
	return ans;
}           

複制

奉上一個完整代碼，可以直接根據提示計算

#include<bits/stdc++.h>
using namespace std;

double cal(double **det,int n)//det-行列式，n:行列式的階數
{ 
   
	double detVal = 0;//行列式的值
	
	if(n == 1)//遞歸終止條件 
	return det[0][0]; 
	
	double **tempdet = new double *[n-1];//用來存儲餘相應的餘子式
	 for(int i=0;i<n-1;i++)
	  tempdet[i] = new double[n-1];
	for(int i=0;i<n;i++)//第一重循環，行列式按第一行展開 
	{ 
   
		for(int j=0;j<n-1;j++)
		for(int k=0;k<n-1;k++)
		{ 
   
			if(k <i)
			tempdet[j][k]=det[j+1][k] ;
			else
			tempdet[j][k]=det[j+1][k+1];
		}
		detVal += det[0][i] * pow(-1.0,i) * cal(tempdet,n-1);
	
	 } 
	 return detVal;
} 
int main()
{ 
   
	int n;
	cout<<" 輸入行列式的階數："; 
	cin >> n;//輸入行列式的階數 
	double **det = new double *[n];//需要動态記憶體 
	for(int i=0;i<n;i++)
       det[i] = new double[n];
	  

	
	cout<<" 輸入行列式："<<endl;
    for(int i=0;i<n;i++)
    for(int j=0;j<n;j++)
     cin >> det[i][j];
     
     cout<<" 該行列式的值為："<<cal(det,n);
	
}           

複制

思路二——逆序數全排列

思路三——初等變換

調試分析

第一種方法在精度上較好，但計算的階數有限；後兩者運算速度會比較好。但是本人最近較忙，後兩者暫未給出（不要打我）- . -。

做題時用第一種方法完全可以幫你解決線性代數的問題。

實作線代其它操作的參考連結

• 線性代數行列式求值/矩陣相乘/求矩陣的逆，一個c++程式全部解決
• 線性代數矩陣乘法用C++代碼實作
• 讓c++程式助你輕松求矩陣的逆

釋出者：全棧程式員棧長，轉載請注明出處：https://javaforall.cn/128986.html原文連結：https://javaforall.cn