大家好,我是快快。今天為大家講解幾道Python應用在
高中資訊技術
中的經典題目。
一、解析“雞兔同籠”問題
“雞兔同籠”最早記載于1500多年前的中國古代數學著作《孫子算經》中的“卷下”第31題(後傳至日本演變為“鶴龜算”),原題為:“今有雉兔同籠,上有三十五頭,下有九十四足,問雉兔各幾何?”意思是“雞和兔的總頭數是35,總腳數是94,雞和兔各有幾隻?”。
1.問題求解
假設雞有x隻,兔有y隻,根據題意列方程為:
x+y=35,2x+4y=94。
求解,得:x=23,y=12;即雞有23隻(46隻腳)、兔有12隻(48隻腳)。 複制
2.Python程式設計求解
如果使用Python語言來編寫程式的話,可使用for循環、range()函數和if條件判斷來完成。
- 先使用“heads = 35”和“feet = 94”兩個指派語句,儲存雞和兔的總頭數和總腳數;
- 接着使用range()函數進行for循環,讓雞的數目從1開始計數加1循環,循環體中的if條件為“2x + 4y ==feet”,即“雞數目的兩倍加兔數目的四倍之和等于總腳數”,條件成立的話,使用print語句進行最終雞兔數目的輸出。
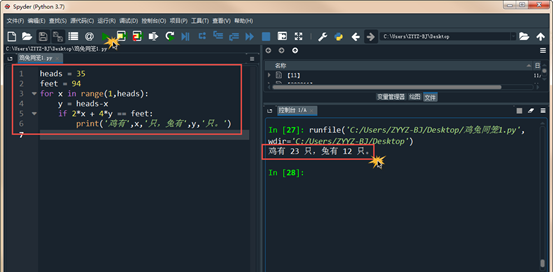
- 儲存程式為“雞兔同籠1.py”,運作結果顯示為“雞有 23 隻,兔有 12 隻。”(如下圖)。
3.更新版“雞兔同籠”問題的Python程式設計求解
考慮到
“雞兔同籠”
原題中所給出的總頭數和總腳數是固定的35和94,是以最終的求解也是固定的
“23隻雞、12隻兔”
。如果将題目進行
“更新”
,雞和兔的總頭數與總腳數均由使用者從鍵盤輸入,仍然來求雞和兔的數目,應該如何編寫程式代碼呢?
首先使用标準輸入函數input來接收使用者從鍵盤上輸入的資訊,比如
“heads = input('請輸入雞和兔的總頭數:')”
和
“feet = input('請輸入雞和兔的總腳數:')”
。但在此需要特别注意的是,Python的input函數接收到的輸入資料是str字元串(雖然表面上看是數字),必須要使用int來轉換成整數型才能進行數學運算,語句為
“heads = int(heads)”和“feet = int(feet)”
。
接下來仍然是使用range()函數進行for循環:
“for x in range(0,(heads+1))”
。此時要充分考慮到使用者所輸入資料的計算結果,很有可能會出現“隻有雞”或“隻有兔”的情況。舉例:使用者輸入的總頭數是10、總腳數是20,運算結果就應該是
“10隻雞、0隻兔”
;或輸入總頭數是10、總腳數是40,運算結果則是
“0隻雞、10隻兔”
。因為在計算機程式設計語言中,數字0總是被看作是最起始的值,Python的清單、字元串和元組等的元素均是從0開始進行索引的。不管是
“0隻雞”
還是
“0隻兔”
,在計算機看來,這都是“雞兔同籠”,隻不過數目是0而已。另外,由于range()函數的兩個參數是“左閉右開”型的區間,即第一個參數是被包括計算在内,而第二個參數卻是不包括在内的(隻計算到它的前一個元素);是以,第二個參數應該設定為“heads+1”,這樣就能在循環時計算到它的前一個元素(即“heads”),也就是“0隻兔”的情況(“x=0”則是“0隻雞”)。
循環體與之前類似,仍然是if條件判斷
“2*x + 4*y == feet”
是否成立,成立的話則使用print輸出結果,然後使用break語句跳出循環。因為不确定使用者從鍵盤上輸入的兩個資料是否恰好為“有效解”——雞和兔的數目必須是整數隻,是以在循環體外應該再添加一個
“if 2*x + 4*y != feet”
判斷語句,将這種無法進行整數結果計算的情況進行提示“輸入的總頭數和總腳數不合法”。沒有該print語句的話,程式也能正常運作,但對于這種
“意外”
沒有任何提示,程式缺少必要的友好性。
最後将程式儲存為
“雞兔同籠2.py”
,運作幾次進行測試,輸入的總頭數和總腳數包括原題目中的
“35、94”
、雞兔各為0隻、
“30、110”
四種合法數值,程式均輸出了正确的計算結果;最後一個測試輸入
“8、100”
,結果就提示“輸入不合法”(如下圖)。
二、解析“Fibonacci數列”問題
Fibonacci(音譯為:
斐波那契
)數列又稱
“黃金分割數列”
,最早是由意大利數學家Fibonacci以兔子繁殖為例引入,是以又稱“兔子數列”。其規則為:數列的第0項是0,第1項是第一個1,從第三項開始,每一項均等于前兩項之和,即:0,1,1,2,3,5,8,13,21……
1.Fibonacci數列的數學解析
一般而言,兔子在出生兩個月之後就會有繁殖能力,一對兔子每月能生出一對小兔子。假設兔子不死亡,一年之後會繁殖出多少對兔子?經分析後不難發現,成年兔子的對數符合這樣的函數定義:
F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N) 複制
如何使用Python程式設計來求解這樣的Fibonacci數列呢?
2.正常的Python“遞歸”程式設計求解
“遞歸”
即函數在運作過程中不斷地直接或間接調用自身的一種算法,比如在Python中通過
“def fib1(n):”
來定義fib1()函數,其主體内容為
“三分支”
結構:前兩種(if和elif)通過判斷參數n是0還是1來分别對應Fibonacci數列的前兩項0和1,二者均通過return語句來傳回對應的數值。注意判斷條件中的雙等号的含義是
“等于”
,一個等号是“指派”運算。第三個分支(else)是
“return fib1(n-1)+fib1(n-2)”
,意思是遞歸運算傳回該項前兩項值的和:F(n)=F(n-1)+F(n-2)。
最後使用
“print('一年之後會繁殖出的兔子對數為:',fib1(12))”
來輸出運算結果,其中的
“fib(12)”
作用是調用fib1()函數,參數為12(一年的月數)。儲存程式為fibonacci1.py,運作後得到結果是144(如下圖)。
3. “更新版”Python程式設計求解
Python支援多變量在一行語句中同時指派的運算,比如
“x,y=y,x”
,意思是x和y這兩個變量的值進行“互換”。對于這種兩個變量進行值互換的運算,其它程式設計語言幾乎都是通過第三方變量來“暫存”中間資料的方式來完成的,例如最初有
“x=3”和“y=4”
兩個指派語句,分别将3和4這兩個資料給變量x和y;接着需要再通過三個指派語句完成x和y資料的互換:
“z=x”、“x=y”和“y=z”
,意思分别是`“将x的值(3)給z”、“将y的值(4)給x”和“将z的值(3)給y”,此時x的值變成4、y的值變成3。
如果使用Python的多變量同時指派方法來程式設計,就可以通過
“def fib2(n):”
來定義fib2()函數。首先通過
“a,b = 0,1”
語句,實作變量a和b同時被分别指派0和1,對應Fibonacci數列的前兩項;接着使用for循環和range()函數
“for i in range(n):”
,其循環體為
“a,b = b,a+b”
,意思是将b的值給a、将a+b的值給b,實作之前使用遞歸算法完成的第三項及之後項的Fibonacci數列運算;for循環體結束後,通過“return a”語句将變量a的值傳回;最後仍是通過print語句的
“fib2(12)”
來調用函數計算并輸出,儲存程式為fibonacci2.py,運作結果仍是144(如下圖)。
4.求任意項Fibonacci數列的Python程式設計
理論上講,Fibonacci數列的值是無窮的,如何使用Python程式設計來實作輸出Fibonacci數列任意項?仍然可以先通過input函數來接收使用者從鍵盤上輸入的
“要求”
,注意一定要使用int()函數将該字元串型資料轉換為整數型資料;接着定義fib3()函數,内容與上面的fib2()完全相同,同樣是傳回a的值;然後使用print語句輸出提示資訊,再同樣是通過for循環加range()函數,循環體内的
“print(fib3(i),end=' ')”
是調用fib3()函數,其中的
“end=' '”
作用是控制列印輸出的各項Fibonacci數列值之間使用一個空格來分隔(預設是回車)。将程式儲存為fibonacci3.py,運作測試,分别嘗試輸入10、20和50,程式就會根據要求輸出Fibonacci數列的前10、20和50個數值(如下圖)。
三、解析“棋盤米粒倍增”和“九九乘法表”問題
印度有個古老傳說:舍罕王打算獎賞國際象棋的發明人——西薩宰相,在被問及想要得到的賞賜時,宰相回答說:“在棋盤的第1格放1粒大米,第2格放2粒,第3格放4粒,之後的每一格中的米粒數目都是相鄰前一格的兩倍,一直放到最後的第64格,我隻要這一棋盤的大米。”
最初國王不以為然,但最終的結果卻是舉全國之力都無法填滿這個棋盤。果真是這樣嗎?我們使用Python程式設計來解決這個
“棋盤米粒倍增”
問題。
1.正常的循環求和法
首先通過
“sum = 0”
語句建立并為變量sum指派為0,準備存放最終的米粒數目;接着使用for循環:
“for i in range(64):”
,其中的range()函數負責提供從0到63共64個循環計數;由于每格中米粒的數目可表示為
“2的(n-1)次方”
,是以循環體語句為
“sum += 2 ** i”
,将每次循環得到的該格子中米粒的數量與之前所有格子中米粒的數量和進行求和;循環結束後通過print語句将求和結果輸出。
将程式儲存為chessrice1.py,運作後得到結果(如下圖):
棋盤米粒的總數為:18446744073709551615 粒。
2.使用清單推導式計算
Python的清單推導式在邏輯上等同于循環語句,優點是形式簡潔且速度快,它能夠以非常簡潔的方式對清單(或其他可疊代對象)中的元素進行周遊、過濾或再次計算,進而快速生成滿足特定需求的清單。
Python的清單推導式可分解為
“表達式+循環”
兩部分,比如通過
“sum = sum([2**i for i in range(64)])”
這一個語句即可完成所有64格子中米粒的數量求和,其中的“2**i”即
“表達式”
部分,作用是計算每格中的米粒數量;後面的“for i in range(64)”是
“循環”
部分,作用是控制完成從0到63共64次循環;sum變量的指派,是通過内置求和sum()函數來完成的。
之前使用正常循環求和法得到的結果是一個20位長的天文數字,機關是“粒”,不夠直覺。經查詢,1千克大米約有52000粒,通過
“mass = int(sum / 52000000)”
語句,将這些大米的數目轉換成機關為“噸”并進行求整,指派給mass變量,最後列印輸出。将程式儲存為chessrice2.py,運作後得到結果(如下圖):
棋盤米粒的總數為:18446744073709551615 粒。
這些米粒的總品質為:354745078340 噸。
米粒總數的計算結果與循環求和法一緻,它們的總品質是個12位數字,約是3547.5億噸!當時,國王無論如何也拿不出數量如此龐大的大米,根本就填不滿宰相的棋盤。
3.兩種方法列印“九九乘法表”
不管是使用正常循環求和還是使用清單推導式,我們都可以正确求解“棋盤米粒倍增”問題,二者在各種問題的求解過程中都比較友善,包括循環的嵌套,比如列印“九九乘法表”。
(1)正常的雙層循環嵌套
外層循環語句為
“for i in range(1,10):”
,作用是從1到9循環;
内層循環語句為
“for j in range(1,i+1):”
,同樣是使用range()進行對應次數的循環;
循環體語句為
“print('{0}*{1} = {2}'.format(j,i,i*j),end=' ') ”
,這個print語句用到了Python的format()方法進行字元串格式化,其中的
“{0}”、“{1}”和“{2}”
是位置參數,作用是将後面
“format(j,i,i*j)”
中的三個變量的對應數值進行占位輸出;
“end=' '”
的作用是設定末尾不換行,而不是print的預設“換行”值;内層循環結束後是一個
“print()”
空語句,作用是換行,即列印完同一個乘數(比如同是乘以3)的一行循環後,回車換行。将程式儲存為ninenine1.py,運作後得到“九九乘法表”(如下圖)。
(2)清單推導式循環嵌套
外層循環語句仍為
“for i in range(1,10):”
,内層直接就是一個清單推導式(因為本身就是一層循環):
“print(" ".join(["%d*%d=%-2d"%(j,i,j*i) for j in range(1,i+1)]))”
。這個print語句中的“join()”方法是将序列中的元素以指定的字元連接配接生成一個新字元串,依次連接配接到前面的" "空串後面;其中的
“%d”
的作用是将資料按照整型格式化輸出,“-”表示左對齊,“2”表示數字不足兩位時進行位數補齊(不足位置用空格)。
清單推導式後面的循環部分是
“for j in range(1,i+1)”
語句,與正常雙層循環嵌套的内層循環語句完全相同。将程式儲存為ninenine2.py,運作後,同樣也得到了“九九乘法表”(如下圖)。
四、多法解析“随機抽獎”問題
假設要從10000個人中随機抽取出10人作為
“中獎者”
,每人對應一個0-9999中的整數,要求使用Python程式設計按從小到大的順序輸出中獎者數字代号。類似的“随機抽獎”程式一般均需要先導入random子產品,然後借助其中的randint()、shuffle()和sample()等函數進行随機數的選取;最後使用清單或集合對資料進行存儲、排序和輸出。
1.randint()生成随機整數後進行in成員運算判斷
首先,通過“import random”導入random子產品(下同);
接着,建立空清單“my_list1 = []”;建立while循環結構,判斷條件為
“len(my_list1) <= 10”
,即清單my_list1中元素的個數達到10為止(通過len()檢測清單的長度);在循環體中,第一條語句為
“x = random.randint(0,9999)”
,變量x取值為0-9999中的随機某個整數(包括0和9999);條件判斷語句
“if x not in my_list1”
的作用是,檢視生成的随機數x是否在清單my_list1中,防止多次生成的随機數中有重複值出現;如果不重複,則使用append()方法将x追加到清單my_list1中:
“my_list1.append(x)”
;當循環結束時,清單my_list1中就會儲存有10個0-9999間的不重複資料。
最後,通過sorted()函數對清單my_list1進行預設參數排序(升序):
“my_list2 = sorted(my_list1)”
,得到的清單my_list2就是從小到大順序中獎号碼,再使用print()輸出結果即可。運作程式,得到了10個“中獎”号碼(如圖10)。
2.randint()生成随機整數後存入集合“去重”
與法1類似,隻不過是使用集合而非清單來存儲生成的随機數:
“my_set = set()”
,建立一個空集合;接着,仍然是在while循環中,通過randint生成0-9999間的某随機數,再将它追加到集合my_set中。由于集合中的元素是不可能存在重複資料的,是以不必像法1中的清單元素進行in成員運算判斷,相當于直接進行了“去重”操作。循環結束後,仍然是使用sorted()函數進行排序并儲存至清單my_list中,進行print列印輸出(如下圖)。
3.shuffle()随機排序後進行“切片”
首先建立清單my_list1,其值為
“list(range(10000))”
,通過list()将0至9999共10000個資料儲存至清單my_list1中;接着使用random中的shuffle(),将清單my_list1中的資料進行随機排序:
“random.shuffle(my_list1)”
;
然後對清單my_list1進行切片操作,任意截取出10個資料,比如“my_list1[:10]”是指從索引的第0個切至第9個(當然也可以使用
“my_list2 = my_list1[99:109]”
,意思是從第99個切至第109個),将它們存入清單my_list2中;仍然是使用sorted()函數進行排序并儲存至第3個清單my_list3中,進行print列印輸出(如下圖)。
4.sample()随機多個“取樣”
Random中的sample()功能是從序列中随機多個
“取樣”
。首先建立清單my_list1,其值為從0-9999中随機抽取10個不重複的資料:
“my_list1 = random.sample(range(10000),10)”
;然後就可以使用sorted()函數進行排序,将結果儲存至清單my_list2中,最後進行print列印輸出(如下圖)。
5. numpy中的random.choice()随機項提取
Numpy中有個
random.choice()
,可以随機從指定清單中提取若幹個元素。
首先,通過“import numpy as np”導入numpy;
接着建立清單my_list1,存儲的資料是0-9999共10000個資料:
“my_list1 = list(range(10000))”
;建立清單my_list2,值為從清單my_list1中随機提取10個不重複的資料:
“my_list2 = np.random.choice(my_list1,10,replace=False)”
,其中的參數“replace=False”即為控制随機數“不重複”。
最後,使用
sorted()
函數進行排序并儲存至第3個清單my_list3中,進行print列印輸出即可(如下圖)。
五、多法解析“自幂數”問題
在程式設計語言的學習過程中,有一道經典的
“水仙花數”
求解問題,即某個三位整數每個數位上數字的三次幂之和等于它本身,比如
“153 = 1^3 + 5^3 + 3^3”
。其實,水仙花數隻是“自幂數”的一種,類似的還有四位數的“四葉玫瑰數”、五位數的“五角星數”、六位數的“六合數”等等。
Python文法靈活,可以使用多種方法程式設計來完成自幂數的求解,在此略舉幾種水仙花數的程式設計方法:
1.“整除”和“求餘”數位分解法
在Python中,運算符“//”代表
“整除”
運算,即求“整商”;而運算符“%”則是進行“求餘”,利用這兩種運算符可以将一個多位數的各位數字“分解”提取。
在判斷一個三位數是否為水仙花數時,首先建構循環結構“for i in range(100,1000):”,百位上的數字提取方法是通過“bai_wei = i//100”求
“整商”
來完成,比如計算“365//100”,結果就是“3”;十位上的數字提取方法是“shi_wei = (i%100)//10”,即先以100為除數進行“求餘”,再将這個中間結果除以10求“整商”,比如計算“(365%100)//10”,會先得到餘數65,然後計算“65//10”得到6;個位上的數字提取方法是“ge_wei = i%10”,即除以10求餘數,比如“365%10”的結果是5。
循環中的if判斷條件是“bai_wei3 + shi_wei3 + ge_wei**3 == i:”,即各數位上的數字的三次方之和與該數相等。最後,通過print列印輸出變量i的數值,結果得到四個水仙花數:153、370、371和407(如下圖)。
2.三層循環嵌套法
因為水仙花數是對一個三位數進行判斷,是以直接建構三層循環嵌套來實作從100到999的順序遞增。最外層的
“for bai_wei in range(1,10):”
控制百位數字循環,注意要從1開始(range()中的起始值和終止值參數為“左閉右開”區間);中間層的十位數字循環是
“for shi_wei in range(0,10):”
;内部的個位數字循環是“for ge_wei in range(0,10):”,變量my_data是計算存儲每個三位數的數值大小,即“bai_wei100+shi_wei10+ge_wei”;判斷條件與之前相同,最後也是列印輸出結果,同樣會得到四個水仙花數:153、370、371和407(如下圖)。
3.map()函數映射法
如果充分利用Python中的各種内置函數,比如
map()
映射函數,可以非常巧妙地快速“提取”出每個多位數上各數位的數字。首先,同樣是通過“for i in range(100,1000):”建構出循環結構;然後使用
“序列解包”
的方式,同時為三個變量指派——“bai_wei,shi_wei,ge_wei = map(int,str(i))”,借助map()函數将每個三位數先通過“str(i)”轉換為字元串,再将int()函數映射至剛剛生成的字元串序列(疊代對象),就
“還原”
得到了三個整形數字,分别指派給三個對應的變量。
接下來仍是使用相同的判斷語句和print()輸出語句,同樣會得到四個水仙花數:153、370、371和407(如下圖 )。
六、多法解析“均勻浮點數生成”問題
衆所周知,在Python中可構造“for i in range(100)”語句來執行100次循環,因為“range(100)”就相當于“range(0,100,1)”,是以1為步長、“左閉”(包括0)“右開”(不包括100)的;如果在該循環中被執行的語句是“print(i,end=' ')”的話,那就會列印輸出從0、1、2……98、99共100個整數。按照這個規律,是否可以使用range()函數來生成類似的均勻浮點數呢?比如從0.00、0.01、0.02……0.98、0.99共100個浮點數。如果直接構造“for i in range(0,1,0.01)”,Python就會給出“TypeError: 'float' object cannot be interpreted as an integer”的錯誤提示,意思是“類型錯誤:浮點型對象不能解釋為整數型”,因為range()函數接收的參數必須是整數(可以是負數),而不能直接處理float浮點數。那麼,如何解決均勻浮點數生成問題呢?
1.while循環控制變量i自增
首先建立并給變量i指派為0.00;接着構造“while i <= 1.00:”循環,其中的第一條語句為
“print('%.2f'%i,end=' ')”
,即以一個空格分隔并保留兩位小數輸出變量i的值;第二條語句為
“i += 0.01”
,即控制i的自增,步長為0.01。運作程式,得到了從0.00到0.99共100個均勻浮點數(如下圖)。
2.使用清單推導式
Python的清單推導式非常靈活,能夠以非常簡潔的方式來快速生成滿足特定需求的清單。比如直接使用一條
“my_list = [i/100 for i in range(100)]”
語句,即可在清單my_list中得到符合要求的100個浮點數,其實就是将“for i in range(100)”所得到的0-99分别進行了“i/100”的計算。最後再使用for循環以同樣的方式來列印輸出,同樣也得到了100個均勻浮點數(如下圖)。
3.借用numpy庫中的arange()
numpy庫中有個與Python的
range()
函數功能類似的
arange()
,它是支援浮點數運算的,而且同樣是使用
“初始值、終值、步長”
三個類似的參數進行調用。在使用“import numpy as np”語句以np為别名導入numpy庫之後,再使用“my_list = list(np.arange(0,1,0.01))”語句,即可将arange()生成的ndarray數組對象轉換為清單資料。最後,同樣是使用for循環列印輸出my_list中的所有元素,就得到了100個均勻浮點數(如下圖)。
4.自定義函數使用yield表達式
既然Python内置的range()函數不提供對浮點數的運算,那我們就可以自定義一個float_data()函數,三個參數依次為start、end和step,同樣是對應
“初始值、終值、步長”
。函數中使用變量i來接收初始值,然後通過while循環(當i<end時)中的“yield i”來向外傳回i的值,當然還要有變量i的步長自增語句:
“i += step”
。
在主程式中調用float_data()函數,接收到的資料存儲至變量my_generator中,最後仍然是通過for循環來将它們列印輸出,也可以得到100個均勻浮點數(如圖22)。
四種方法均能實作均勻浮點數的生成,大家可根據自己的程式設計習慣來使用。當然,如果想生成的是0.000、0.001、0.002……0.999這樣的千分位均勻浮點數,隻要在程式中将步長修改為0.001、print輸出
“%.3f”
以及方法2中将“i/100”修改為“i/1000”等等即可。