天天看點
傳回

CS231n 之 SVM

SVM模型原理

作者：JackMeGo

連結：https://www.jianshu.com/p/6340c6f090e9

來源：簡書

簡書著作權歸作者所有，任何形式的轉載都請聯系作者獲得授權并注明出處。

SVM通過平面将空間中的執行個體劃分到不同的類别，進而實作分類。這裡的空間包括二維空間，三維空間，一直到高維空間，具體的維數等于執行個體的特征數量，如果我們待分類的圖檔是32323（長寬分别是32個像素，RGB3個顔色通道）維的，那麼圖檔所處的空間就是3072維的空間。在這個高維空間，我們通過由權重向量W和偏置項b确定的一個（實際上是一組）超平面來将圖檔進行分類。為了可視化，我們将多元空間壓縮到二維空間，那麼就是下面的圖像：

CS231n 之 SVM

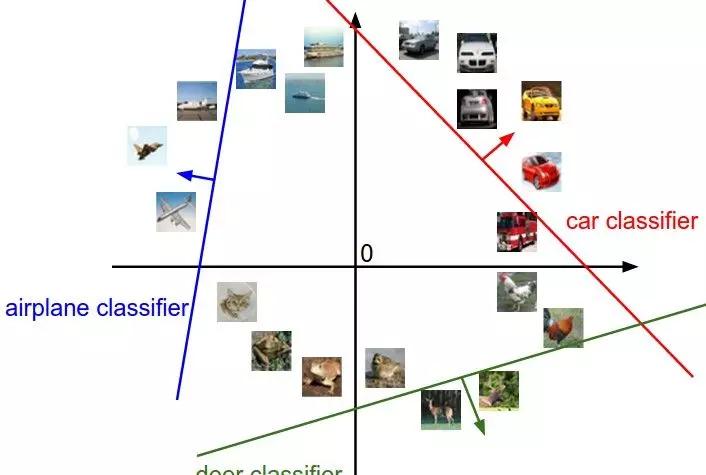
這裡每一個平面都将整個高維空間劃分成兩部分，平面的一側是某一類圖檔，另一側是這個類别之外的其他圖檔。比如紅色的平面一側是汽車這個類别，另一側是非汽車類别。每一個類别都對應一個平面，這些平面互相之間不存在關聯，利用SVM模型進行分類的目的就是确定這樣一組平面，使得同一類盡可能劃分在該類對應的平面的一側，其他類盡可能在另一側，而且兩種類别離平面的距離越大越好（平面盡可能把兩類分的更開），這是SVM模型的思路。

所有這些類别對應的平面通過下面的矩陣唯一确定：

CS231n 之 SVM

其中改變W可以使平面旋轉，而改變b使平面平移。如果b為0，此時W*0=0,那麼平面會經過原點。

SVM的一種直覺解釋

SVM模型圖像分類可以看做給每一種圖像的類别生成一個圖像模闆，然後拿待分類的圖像和這個圖像模闆做内積，計算他們的相似度，相似度最高的類别就是分類類别。根據這個思想，生成的權重向量可視化如下：

CS231n 之 SVM

可以看出，這些圖像模闆比較能夠代表某種類别的共性，比如car類别是一輛紅色的車的形象，而horse類型是左右兩匹馬的形象，這些是集合了所有訓練樣本得出的模闆。從這個角度，SVM可以看做KNN模型的一種簡化，KNN模型對一張圖檔分類時需要和所有訓練樣本做比較，而SVM隻需要和抽象出來的每個類别下的一個圖像模闆做比較即可，顯然更高效。

損失函數

SVM模型有多種不同的實作，差別主要展現在損失函數的定義上，可以根據實作分為：

  • 經典SVM

經典SVM模型核心思路是找一個超平面将不同類别分開，同時使得離超平面最近的點的距離最大，這樣能保證即使是最難區分的點，也有較大的确信度将它們分開，可以通過數學方法證明這樣的超平面是唯一存在的（參考《統計學習方法》）。

  • Structured SVM

    而Structured SVM 可以看做是對經SVM模型的泛化，則是通過事先構造損失函數來求解一個統計上的最優解，該方式避免了經典SVM簡單粗暴的懲罰方式(比如分錯懲罰1，分對懲罰0)，對分類錯誤程度不同的樣本進行程度不同的懲罰，對實際訓練資料中噪音資料具有更大的容錯性，分類效果也更好。

    Structured SVM模型中我們使用折頁損失函數（hinge loss function）來計算損失值。折頁損失函數可以有不同的表示，我們使用如下的表示：

CS231n 之 SVM

折頁損失

某個樣本經過f映射後會得到N個分值，對應為N個類别的得分。這N個類别中隻有一個類别是這個樣本的實際類别，用yi表示。類别yi的分值用Syi表示，其他不正确的類别得分用Sj表示，Δ是一個距離門檻值。從這個折頁損失函數的定義可以看出，這個樣本在N個類别上的得分，有些會産生損失，有些不會：

  1. 得分比正确類别yi高的類别肯定會産生損失，對于這些類别Sj>Syi，是以Sj-Syi+Δ>0，這說明正确分類的分值應該是最高的。
  2. 得分比正确類别yi低的那些類别也有可能會産生損失，如果Sj<Syi，但是他們的距離太近，小于一個Δ值，也就是Syi-Sj<Δ，此時Sj-Syi+Δ>0，也會貢獻損失。這說明我們不僅希望錯誤類别得分比正确類别低，而且要至少低一個Δ值。

損失函數加入正則化項

損失函數數值的大小跟權重參數W成正比，對于同一個樣本，成倍的擴大權重向量W會導緻損失值成倍增加，這是損失值的變化沒有意義的，為了限制這種變化，我們在損失函數中添加一個正則化項，L2正則化項定義如下：

CS231n 之 SVM

正則化損失項

這樣，當權重擴大的時候會導緻損失擴大，然後通過反向傳遞作用回權重矩陣W，進而對過大的權重加以修正，避免了權重向量的單向增大。

在資料損失(data loss)的基礎上，添加了L2正則化損失(regularization loss)項的損失函數如下：

CS231n 之 SVM

加入L2正則項的損失函數

舉個例子，假設輸入向量x=[1, 1, 1, 1], 權重向量W1=[1, 0, 0, 0]，權重向量 W2=[0.25, 0.25, 0.25, 0.25]，W1x = 1，W2x=1，可以看到兩個内積是一樣的。但是W1的L2懲罰是1，而W2的L2懲罰是0.25，是以會更傾向于選擇W2。直覺上解釋就是L2懲罰希望各個權重分量是比較均衡的，而不是某些分量權重一支獨大，因為這樣更能利用起樣本中各個特征，而避免過度依賴某幾個特征。

展開損失函數：

CS231n 之 SVM

損失函數

這裡Δ和λ是兩個超參數，它們的值是如何确定的？

  • Δ控制的是損失函數中資料損失部分，λ控制正則化損失部分，

這兩個變量對損失的貢獻是正相關的，實際上它們兩個共同控制着損失函數中資料損失和正則化損失的權衡，是以同時調整兩個值是沒意義的。實際使用中，我們一般設定Δ=1為固定值，而通過交叉驗證的方式調整λ值。也就是選擇不同的λ，通過訓練資料進行模型訓練，在驗證集上驗證，然後調整λ，看看結果是不是更優，最終選擇一個最優的λ，确定最優的模型。

梯度下降和梯度檢驗

定義好損失函數後，我們就可以通過梯度下降的方法利用訓練集來更新權重參數，也就是模型訓練的過程。

SVM模型中有兩個參數，權重矩陣W和偏移量b，我們可以将這兩個變量合并起來訓練，将b作為一列添加在W後面，同時在輸入向量X裡添加一行，值為1，這樣就可以值訓練一個合并後的矩陣：

CS231n 之 SVM

W和b合并技巧

梯度下降的核心就是計算損失函數對各個權重分量的梯度，然後根據梯度更新各個權重。

對SVM損失函數進行梯度計算，根據損失函數定義，一個樣本梯度的計算分為正确分類權重對應行和不正确分類權重對應的行兩種情況，資料損失項的梯度為下面兩個公式：

CS231n 之 SVM

錯誤分類項的梯度

CS231n 之 SVM

正确分類項的梯度

正則化損失項的梯度很簡單，2Wij，可以在正則化損失前面添加一個參數0.5，這樣可以将正則化損失項的梯度變為Wij，在代碼中會講到這一點。

這樣我們就得到了梯度的解析解，在利用梯度進行權重更新之前，我們還需要驗證一下這個梯度解析解是不是正确，方法就是利用梯度的定義求解權重向量分量的梯度的數值解，比較數值解和解析解，如果兩者的差距非常小，說明解析解是正确的，否則說明有誤，需要查找錯誤。

梯度數值解的計算很簡單，根據下面梯度的公式，在給定的樣本和權重矩陣下，計算輸出，然後讓權重矩陣的變量發生微小的變化，再計算輸出，兩次輸出的內插補點除以變化量就是權重矩陣的梯度：

CS231n 之 SVM

梯度的公式

檢驗沒問題後，就可以進行訓練了。

圖像預處理

通常我們會将所有圖檔，包括訓練資料和待分類資料，減去圖檔每個位置像素的均值，使得資料中心化，這樣可以提高模型的效果。同時，也可以對中心化後的資料歸一化處理，使其分布在[-1, 1]區間，進一步優化模型效果。

小批量資料梯度下降（Mini-batch gradient descent）

相比于每次拿一個樣例資料進行梯度更新，每次使用一個小批量資料進行梯度更新能夠更好的避免單個樣本資料的擾動，可以顯著提高模型訓練的效率，損失的變化更加平滑，使得模型更快的收斂。具體操作方法是一次計算一個批量的資料的結果，如256個樣本，計算每個結果下權重矩陣每個變量的梯度。對于每個權重分量，累加256個梯度值，求均值作為該分量的梯度，更新該分量。

代碼實作

完整的代碼在github，包括訓練資料，測試資料的擷取，圖像預處理等，這裡隻給出計算損失和梯度的關鍵代碼：

def svm_loss_vectorized(W, X, Y, reg):
    """
    :param X: 200 X 3073
    :param Y: 200
    :param W: 3073 X 10
    :return: reg: 正則化損失系數（無法通過拍腦袋設定，需要多試幾個值，交叉驗證，然後找個最優的）
    """
    delta = 1.0
    num_train = X.shape[0]

    patch_X = X  # 200 X 3073
    patch_Y = Y  # 200

    patch_result = patch_X.dot(W)  # 200 X 3073 3073 X 10 -> 200 X 10

    sample_label_value = patch_result[[xrange(patch_result.shape[0])], patch_Y]  # 1 X 200 切片操作，将得分array中标記位置的得分取出來作為新的array
    loss_array = np.maximum(0, patch_result - sample_label_value.T + delta)  # 200 X 10 計算誤差
    loss_array[[xrange(patch_result.shape[0])], patch_Y] = 0  # 200 X 10 将label值所在的位置誤差置零

    loss = np.sum(loss_array)

    loss /= num_train  # get mean

    # regularization: 這裡給損失函數中正則損失項添加了一個0.5參數，是為了後面在計算損失函數中正則化損失項的梯度時和梯度參數2進行抵消
    loss += 0.5 * reg * np.sum(W * W)

    # 将loss_array大于0的項（有誤差的項）置為1，沒誤差的項為0
    loss_array[loss_array > 0] = 1  # 200 X 10

    # 沒誤差的項中有一項是标記項，計算标記項的權重分量對誤差也有共享，也需要更新對應的權重分量
    # loss_array中這個參數就是目前樣本結果錯誤分類的數量
    loss_array[[xrange(patch_result.shape[0])], patch_Y] = -np.sum(loss_array, 1)

    # patch_X:200X3073  loss_array:200 X 10   -> 10*3072
    dW = np.dot(np.transpose(patch_X), loss_array)  # 3073 X 10
    dW /= num_train  # average out weights
    dW += reg * W  # regularize the weights

    return loss, dW

該模型的準确率在38%左右，是以SVM模型分類效果還是比較差的，通過更複雜的神經網絡，或者CNN等模型，可以實作95%以上的準确率。不過SVM是神經網絡的基礎，了解了SVM的原理，再學習神經網絡就比較容易觸類旁通。

GIT 完整代碼：https://github.com/452896915/cs231n_course_homework

作業講解

求損失Loss

  • 多分類線性SVM：y=Wx
  • Hinge Loss（Max margin），margin=1：
    CS231n 之 SVM
    CS231n 之 SVM
CS231n 之 SVM

舉個簡單的例子

CS231n 之 SVM

注意：這個式子中隻有錯誤的分類才會産生loss，即j=i 正确分類是沒有loss的。 設定Delta：超參數 ΔΔ應該被設定成什麼值？需要通過交叉驗證來求得嗎？在絕大多數情況下該超參數設為 Δ=1.0Δ=1.0 都是安全的。

實作代碼如下：

scores=X.dot(W)
margin=scores-scores[np.arange(num_train),y].reshape(num_train,1)+1
margin[np.arange(num_train),y]=0.0#正确的這一列不該計算，歸零
margin=(margin>0)*margin
loss+=margin.sum()/num_train
loss+=0.5*reg*np.sum(W*W)#乘0.5，因為後面是平方，求導時有一個2可以與0.5相乘為1

求梯度dW

  • Loss計算公式：
    CS231n 之 SVM
  • 梯度：
    CS231n 之 SVM
    其中 11 是一個示性函數，如果括号中的條件為真，那麼函數值為 11 ，如果為假，則函數值為 00 。雖然上述公式看起來複雜，但在代碼實作的時候比較簡單：隻需要計算沒有滿足邊界值的分類的數量（是以對損失函數産生了貢獻），然後乘以 xixi 就是梯度了。注意，這個梯度隻是對應正确分類的 WW 的行向量的梯度，那些 j≠yij≠yi 行的梯度是：
    CS231n 之 SVM
    具體實作代碼： 
margin=(margin>0)*1
row_sum=np.sum(margin,axis=1)
margin[np.arange(num_train),y]=-row_sum
dW=X.T.dot(margin)/num_train+reg*W

參見 CS231n課程學習筆記（二）——SVM的實作 https://blog.csdn.net/stalbo/article/details/79379070

神經網絡
上一篇: Maven NetBeans（上）
下一篇: SpringBoot使用JWT入門級示例準備工作：在pom.xml中映入依賴JWT簡單使用示例：測試一下：

繼續閱讀