樹結構
數組存儲方式的分析
優點:通過下标方式通路元素,速度快。對于有序數組,還可使用二分查找提高檢索速度。
缺點:如果要檢索具體某個值,或者插入值(按一定順序)會整體移動,效率較低
鍊式存儲方式的分析
優點:在一定程度上對數組存儲方式有優化(比如:插入一個數值節點,隻需要将插入節點,連結到連結清單中即可,删除效率也很好)。
缺點:在進行檢索時,效率仍然較低,比如(檢索某個值,需要從頭節點開始周遊)
樹存儲方式的分析
能提高資料存儲,讀取的效率, 比如利用 二叉排序樹(Binary Sort
Tree),既可以保證資料的檢索速度,同時也可以保證資料的插入,删除,修改的速度
二叉樹
二叉樹周遊
樹有很多種,每個節點最多隻能有兩個子節點的一種形式稱為二叉樹。 二叉樹的子節點分為左節點和右節點。
二叉樹周遊的說明
前序周遊: 先輸出父節點,再周遊左子樹和右子樹
中序周遊: 先周遊左子樹,再輸出父節點,再周遊右子樹
後序周遊: 先周遊左子樹,再周遊右子樹,最後輸出父節點
小結: 看輸出父節點的順序,就确定是前序,中序還是後序
二叉樹周遊查找的說明
二叉樹删除
二叉樹的周遊,查找以及删除 代碼
package com.atguigu.tree;
public class BinaryTreeDemo {
public static void main(String[] args) {
//先需要建立一顆二叉樹
BinaryTree binaryTree = new BinaryTree();
//建立需要的結點
HeroNode root = new HeroNode(1, "宋江");
HeroNode node2 = new HeroNode(2, "吳用");
HeroNode node3 = new HeroNode(3, "盧俊義");
HeroNode node4 = new HeroNode(4, "林沖");
HeroNode node5 = new HeroNode(5, "關勝");
HeroNode node6 = new HeroNode(6, "關勝222");
HeroNode node7 = new HeroNode(7, "關勝333");
//說明,我們先手動建立該二叉樹,後面我們學習遞歸的方式建立二叉樹
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
node5.setLeft(node7);
node5.setRight(node6);
binaryTree.setRoot(root);
//測試一把删除結點
// System.out.println("删除前,前序周遊");
// binaryTree.preOrder(); // 1,2,3,5,4
// binaryTree.delNode(5);
// System.out.println("删除後,前序周遊");
// binaryTree.preOrder(); // 1,2,3,4
// binaryTree.postOrder();
// binaryTree.preOrder();
binaryTree.preOrder();
// binaryTree.infixOrder();
// binaryTree.postOrder();
}
}
//定義BinaryTree 二叉樹
class BinaryTree {
//節點提供具體的底層實作方法 樹來提供接口調用
//節點用于遞歸 樹用于調用
private HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
//删除結點
public void delNode(int no) {
if(root != null) {
//如果隻有一個root結點, 這裡立即判斷root是不是就是要删除結點
if(root.getNo() == no) {
root = null;
} else {
//遞歸删除
root.delNode(no);
}
}else{
System.out.println("空樹,不能删除~");
}
}
//前序周遊
public void preOrder() {
if(this.root != null) {
this.root.preOrder();
}else {
System.out.println("二叉樹為空,無法周遊");
}
}
//中序周遊
public void infixOrder() {
if(this.root != null) {
this.root.infixOrder();
}else {
System.out.println("二叉樹為空,無法周遊");
}
}
//後序周遊
public void postOrder() {
if(this.root != null) {
this.root.postOrder();
}else {
System.out.println("二叉樹為空,無法周遊");
}
}
//前序周遊
public HeroNode preOrderSearch(int no) {
if(root != null) {
return root.preOrderSearch(no);
} else {
return null;
}
}
//中序周遊
public HeroNode infixOrderSearch(int no) {
if(root != null) {
return root.infixOrderSearch(no);
}else {
return null;
}
}
//後序周遊
public HeroNode postOrderSearch(int no) {
if(root != null) {
return this.root.postOrderSearch(no);
}else {
return null;
}
}
}
//先建立HeroNode 結點
class HeroNode {
private int no;
private String name;
private HeroNode left; //預設null
private HeroNode right; //預設null
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
//遞歸删除結點
//1.如果删除的節點是葉子節點,則删除該節點
//2.如果删除的節點是非葉子節點,則删除該子樹
public void delNode(int no) {
//思路
/*
* 1. 因為我們的二叉樹是單向的,是以我們是判斷目前結點的子結點是否需要删除結點,而不能去判斷目前這個結點是不是需要删除結點.
2. 如果目前結點的左子結點不為空,并且左子結點 就是要删除結點,就将this.left = null; 并且就傳回(結束遞歸删除)
3. 如果目前結點的右子結點不為空,并且右子結點 就是要删除結點,就将this.right= null ;并且就傳回(結束遞歸删除)
4. 如果第2和第3步沒有删除結點,那麼我們就需要向左子樹進行遞歸删除
5. 如果第4步也沒有删除結點,則應當向右子樹進行遞歸删除.
*/
//2. 如果目前結點的左子結點不為空,并且左子結點 就是要删除結點,就将this.left = null; 并且就傳回(結束遞歸删除)
if(this.left != null && this.left.no == no) {
this.left = null;
return;
}
//3.如果目前結點的右子結點不為空,并且右子結點 就是要删除結點,就将this.right= null ;并且就傳回(結束遞歸删除)
if(this.right != null && this.right.no == no) {
this.right = null;
return;
}
//4.我們就需要向左子樹進行遞歸删除
if(this.left != null) {
this.left.delNode(no);
}
//5.則應當向右子樹進行遞歸删除
if(this.right != null) {
this.right.delNode(no);
}
}
//編寫前序周遊的方法
public void preOrder() {
System.out.println(this); //先輸出父結點
//遞歸向左子樹前序周遊
if(this.left != null) {
this.left.preOrder();
}
//遞歸向右子樹前序周遊
if(this.right != null) {
this.right.preOrder();
}
}
//中序周遊
public void infixOrder() {
//遞歸向左子樹中序周遊
if(this.left != null) {
this.left.infixOrder();
}
//輸出父結點
System.out.println(this);
//遞歸向右子樹中序周遊
if(this.right != null) {
this.right.infixOrder();
}
}
//後序周遊
public void postOrder() {
if(this.left != null) {
this.left.postOrder();
}
if(this.right != null) {
this.right.postOrder();
}
System.out.println(this);
}
//前序周遊查找
/**
*
* @param no 查找no
* @return 如果找到就傳回該Node ,如果沒有找到傳回 null
*/
public HeroNode preOrderSearch(int no) {
System.out.println("進入前序周遊");
//比較目前結點是不是
if(this.no == no) {
return this;
}
//1.則判斷目前結點的左子節點是否為空,如果不為空,則遞歸前序查找
//2.如果左遞歸前序查找,找到結點,則傳回
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.preOrderSearch(no);
}
if(resNode != null) {//說明我們左子樹找到
return resNode;
}
//1.左遞歸前序查找,找到結點,則傳回,否繼續判斷,
//2.目前的結點的右子節點是否為空,如果不空,則繼續向右遞歸前序查找
if(this.right != null) {
resNode = this.right.preOrderSearch(no);
}
return resNode;
}
//中序周遊查找
public HeroNode infixOrderSearch(int no) {
//判斷目前結點的左子節點是否為空,如果不為空,則遞歸中序查找
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.infixOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
System.out.println("進入中序查找");
//如果找到,則傳回,如果沒有找到,就和目前結點比較,如果是則傳回目前結點
if(this.no == no) {
return this;
}
//否則繼續進行右遞歸的中序查找
if(this.right != null) {
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
//後序周遊查找
public HeroNode postOrderSearch(int no) {
//判斷目前結點的左子節點是否為空,如果不為空,則遞歸後序查找
HeroNode resNode = null;
if(this.left != null) {
resNode = this.left.postOrderSearch(no);
}
if(resNode != null) {//說明在左子樹找到
return resNode;
}
//如果左子樹沒有找到,則向右子樹遞歸進行後序周遊查找
if(this.right != null) {
resNode = this.right.postOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
System.out.println("進入後序查找");
//如果左右子樹都沒有找到,就比較目前結點是不是
if(this.no == no) {
return this;
}
return resNode;
}
}
順序存儲二叉樹
順序存儲二叉樹的特點:
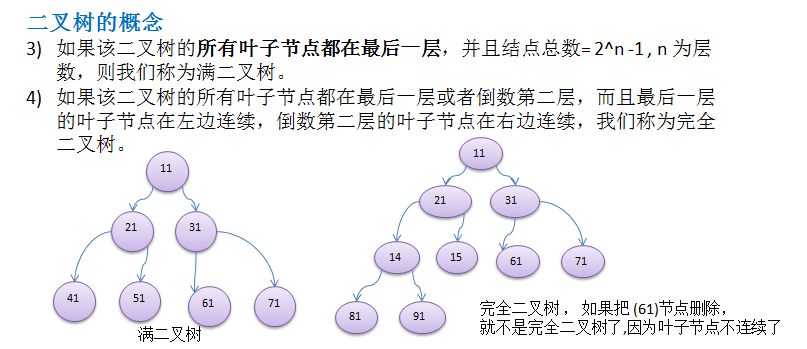
1)順序二叉樹通常隻考慮完全二叉樹
2)第n個元素的左子節點為 2 * n + 1
3)第n個元素的右子節點為 2 * n + 2
4)第n個元素的父節點為 (n-1) / 2
5)n : 表示二叉樹中的第幾個元素(按0開始編号
順序存儲二叉樹應用執行個體
八大排序算法中的堆排序,就會使用到順序存儲二叉樹
代碼
package com.atguigu.tree;
public class ArrBinaryTreeDemo {
public static void main(String[] args) {
int[] arr = { 1, 2, 3, 4, 5, 6, 7 };
//建立一個 ArrBinaryTree
ArrBinaryTree arrBinaryTree = new ArrBinaryTree(arr);
arrBinaryTree.preOrder(); // 1,2,4,5,3,6,7
}
}
//編寫一個ArrayBinaryTree, 實作順序存儲二叉樹周遊
class ArrBinaryTree {
private int[] arr;//存儲資料結點的數組
public ArrBinaryTree(int[] arr) {
this.arr = arr;
}
//重載preOrder
public void preOrder() {
this.preOrder(0);
}
//編寫一個方法,完成順序存儲二叉樹的前序周遊
/**
*
* @param index 數組的下标
*/
public void preOrder(int index) {
//如果數組為空,或者 arr.length = 0
if(arr == null || arr.length == 0) {
System.out.println("數組為空,不能按照二叉樹的前序周遊");
}
//輸出目前這個元素
System.out.println(arr[index]);
//向左遞歸周遊
if((index * 2 + 1) < arr.length) {
preOrder(2 * index + 1 );
}
//向右遞歸周遊
if((index * 2 + 2) < arr.length) {
preOrder(2 * index + 2);
}
}
}
線索化二叉樹
赫夫曼樹
1)給定n個權值作為n個葉子結點,構造一棵二叉樹,若該樹的帶權路徑長度(wpl)達到最小,稱這樣的二叉樹為最優二叉樹,也稱為哈夫曼樹(HuffmanTree),還有的書翻譯為霍夫曼樹。
2)赫夫曼樹是帶權路徑長度最短的樹,權值較大的結點離根較近
赫夫曼樹幾個重要概念和舉例說明
1)路徑和路徑長度:在一棵樹中,從一個結點往下可以達到的孩子或孫子結點之間的通路,稱為路徑。通路中分支的數目稱為路徑長度。若規定根結點的層數為1,則從根結點到第L層結點的路徑長度為L-1
2)結點的權及帶權路徑長度:結點的帶權路徑長度為:從根結點到該結點之間的路徑長度與該結點的權的乘積
3)樹的帶權路徑長度:樹的帶權路徑長度規定為所有葉子結點的帶權路徑長度之和,記為WPL(weighted path
length) ,權值越大的結點離根結點越近的二叉樹才是最優二叉樹。
4)WPL最小的就是赫夫曼樹
構成赫夫曼樹的步驟:
1)從小到大進行排序, 将每一個資料,每個資料都是一個節點 , 每個節點可以看成是一顆最簡單的二叉樹
2)取出根節點權值最小的兩顆二叉樹
3)組成一顆新的二叉樹, 該新的二叉樹的根節點的權值是前面兩顆二叉樹根節點權值的和
4)再将這顆新的二叉樹,以根節點的權值大小 再次排序, 不斷重複 1-2-3-4 的步驟,直到數列中,所有的資料都被處理,就得到一顆赫夫曼樹
例; {13,7,8,3,29,6,1}
代碼實作
package com.atguigu.huffmantree;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class HuffmanTree {
public static void main(String[] args) {
int arr[] = { 13, 7, 8, 3, 29, 6, 1 };
Node root = createHuffmanTree(arr);
//測試一把
preOrder(root); //
}
//編寫一個前序周遊的方法
public static void preOrder(Node root) {
if(root != null) {
root.preOrder();
}else{
System.out.println("是空樹,不能周遊~~");
}
}
// 建立赫夫曼樹的方法
/**
* @param arr 需要建立成哈夫曼樹的數組
* @return 建立好後的赫夫曼樹的root結點
*/
public static Node createHuffmanTree(int[] arr) {
// 第一步為了操作友善
// 1. 周遊 arr 數組
// 2. 将arr的每個元素構成成一個Node
// 3. 将Node 放入到ArrayList中
List<Node> nodes = new ArrayList<Node>();
for (int value : arr) {
nodes.add(new Node(value));
}
//我們處理的過程是一個循環的過程
while(nodes.size() > 1) {
//排序 從小到大
Collections.sort(nodes);
System.out.println("nodes =" + nodes);
//取出根節點權值最小的兩顆二叉樹
//(1) 取出權值最小的結點(二叉樹)
Node leftNode = nodes.get(0);
//(2) 取出權值第二小的結點(二叉樹)
Node rightNode = nodes.get(1);
//(3)建構一顆新的二叉樹
Node parent = new Node(leftNode.value + rightNode.value);
parent.left = leftNode;
parent.right = rightNode;
//(4)從ArrayList删除處理過的二叉樹
nodes.remove(leftNode);
nodes.remove(rightNode);
//(5)将parent加入到nodes
nodes.add(parent);
}
//傳回哈夫曼樹的root結點
return nodes.get(0);
}
}
// 建立結點類
// 為了讓Node 對象持續排序Collections集合排序
// 讓Node 實作Comparable接口
class Node implements Comparable<Node> {
int value; // 結點權值
char c; //字元
Node left; // 指向左子結點
Node right; // 指向右子結點
//寫一個前序周遊
public void preOrder() {
System.out.println(this);
if(this.left != null) {
this.left.preOrder();
}
if(this.right != null) {
this.right.preOrder();
}
}
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
@Override
public int compareTo(Node o) {
// TODO Auto-generated method stub
// 表示從小到大排序
return this.value - o.value;
}
}
赫夫曼編碼
基本介紹
1)赫夫曼編碼也翻譯為哈夫曼編碼(HuffmanCoding),又稱霍夫曼編碼,是一種編碼方式,屬于一種程式算法
2)赫夫曼編碼是赫哈夫曼樹在電訊通信中的經典的應用之一。
3)赫夫曼編碼廣泛地用于資料檔案壓縮。其壓縮率通常在20%~90%之間
4)赫夫曼碼是可變字長編碼(VLC)的一種。Huffman于1952年提出一種編碼方法,稱之為最佳編碼
原理剖析
Ø通信領域中資訊的處理方式1-定長編碼
•i like like like java do you like a java // 共40個字元(包括空格)
•105 32 108 105 107 101 32 108 105 107 101 32 108 105 107 101 32 106
97 118 97 32 100 111 32 121 111 117 32 108 105 107 101 32 97 32 106 97
118 97 //對應Ascii碼
•01101001 00100000 01101100 01101001 01101011 01100101 00100000
01101100 01101001 01101011 01100101 00100000 01101100 01101001
01101011 01100101 00100000 01101010 01100001 01110110 01100001
00100000 01100100 01101111 00100000 01111001 01101111 01110101
00100000 01101100 01101001 01101011 01100101 00100000 01100001
00100000 01101010 01100001 01110110 01100001 //對應的二進制
•按照二進制來傳遞資訊,總的長度是 359 (包括空格)
•線上轉碼 工具
:https://www.mokuge.com/tool/asciito16/
Ø通信領域中資訊的處理方式2-變長編碼
•i like like like java do you like a java // 共40個字元(包括空格)
•d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9 // 各個字元對應的個數
•0= , 1=a, 10=i, 11=e, 100=k, 101=l, 110=o, 111=v, 1000=j, 1001=u,
1010=y, 1011=d 說明:按照各個字元出現的次數進行編碼,原則是出現次數越多的,則編碼越小,比如 空格出現了9 次, 編碼為0
,其它依次類推.
•按照上面給各個字元規定的編碼,則我們在傳輸 “i like like like java do you like a java”
資料時,編碼就是
10010110100…
•字元的編碼都不能是其他字元編碼的字首,符合此要求的編碼叫做字首編碼, 即不能比對到重複的編碼(這個在赫夫曼編碼中,我們還要進行舉例說明,
不捉急)
Ø通信領域中資訊的處理方式3-赫夫曼編碼
•i like like like java do you like a java // 共40個字元(包括空格)
•d:1 y:1 u:1 j:2 v:2 o:2 l:4 k:4 e:4 i:5 a:5 :9 // 各個字元對應的個數
按照上面字元出現的次數建構一顆赫夫曼樹, .()
//根據赫夫曼樹,給各個字元
//規定編碼 , 向左的路徑為0
//向右的路徑為1 , 編碼如下:
o: 1000 u: 10010 d: 100110 y: 100111 i: 101
a : 110 k: 1110 e: 1111 j: 0000 v: 0001
l: 001 : 01
按照上面的赫夫曼編碼,我們的"i like like like java do you like a java" 字元串對應的編碼為
(注意這裡我們使用的無損壓縮)
1010100110111101111010011011110111101001101111011110100001100001110011001111000011001111000100100100110111101111011100100001100001110
長度為 : 133
說明:
1)原來長度是 359 , 壓縮了 (359-133) / 359 = 62.9%
2)此編碼滿足字首編碼, 即字元的編碼都不能是其他字元編碼的字首。不會造成比對的多義性
注意, 這個赫夫曼樹根據排序方法不同,也可能不太一樣,這樣對應的赫夫曼編碼也不完全一樣,但是wpl 是一樣的,都是最小的, 比如:
如果我們讓每次生成的新的二叉樹總是排在權值相同的二叉樹的最後一個,則生成的二叉樹為:
**赫夫曼樹的具體實作代碼**
//可以通過List 建立對應的赫夫曼樹
private static Node createHuffmanTree(List<Node> nodes) {
while(nodes.size() > 1) {
//排序, 從小到大
Collections.sort(nodes);
//取出第一顆最小的二叉樹
Node leftNode = nodes.get(0);
//取出第二顆最小的二叉樹
Node rightNode = nodes.get(1);
//建立一顆新的二叉樹,它的根節點 沒有data, 隻有權值
Node parent = new Node(null, leftNode.weight + rightNode.weight);
parent.left = leftNode;
parent.right = rightNode;
//将已經處理的兩顆二叉樹從nodes删除
nodes.remove(leftNode);
nodes.remove(rightNode);
//将新的二叉樹,加入到nodes
nodes.add(parent);
}
//nodes 最後的結點,就是赫夫曼樹的根結點
return nodes.get(0);
}
最佳實踐-**資料壓縮(**建立赫夫曼樹)
将給出的一段文本,比如 “i like like like java do you like a java” ,
根據前面的講的赫夫曼編碼原理,對其進行資料壓縮處理 ,形式如
“1010100110111101111010011011110111101001101111011110100001100001110011001111000011001111000100100100110111101111011100100001100001110”
步驟1:根據赫夫曼編碼壓縮資料的原理,需要建立 “i like like like java do you like a java”
對應的赫夫曼樹.
我們已經生成了 赫夫曼樹, 下面我們繼續完成任務
1)生成赫夫曼樹對應的赫夫曼編碼 , 如下表: =01 a=100 d=11000 u=11001 e=1110 v=11011
i=101 y=11010 j=0010 k=1111 l=000 o=0011
2)使用赫夫曼編碼來生成赫夫曼編碼資料 ,即按照上面的赫夫曼編碼,将"i like like like java do you like a
java" 字元串生成對應的編碼資料, 形式如下.
1010100010111111110010001011111111001000101111111100100101001101110001110000011011101000111100101000101111111100110001001010011011100
//可以通過List 建立對應的赫夫曼樹
private static Node createHuffmanTree(List<Node> nodes) {
while(nodes.size() > 1) {
//排序, 從小到大
Collections.sort(nodes);
//取出第一顆最小的二叉樹
Node leftNode = nodes.get(0);
//取出第二顆最小的二叉樹
Node rightNode = nodes.get(1);
//建立一顆新的二叉樹,它的根節點 沒有data, 隻有權值
Node parent = new Node(null, leftNode.weight + rightNode.weight);
parent.left = leftNode;
parent.right = rightNode;
//将已經處理的兩顆二叉樹從nodes删除
nodes.remove(leftNode);
nodes.remove(rightNode);
//将新的二叉樹,加入到nodes
nodes.add(parent);
}
//nodes 最後的結點,就是赫夫曼樹的根結點
return nodes.get(0);
}
最佳實踐-資料壓縮(生成赫夫曼編碼和赫夫曼編碼後的資料)
我們已經生成了赫夫曼樹,下面我們繼續完成任務
1)生成赫夫曼樹對應的赫夫曼編碼,如下表:=01a=100d=11000u=11001e=1110v=11011i=101y=11010j=0010k=1111l=000o=0011
2)使用赫夫曼編碼來生成赫夫曼編碼資料,即按照上面的赫夫曼編碼,将"ilikelikelikejavadoyoulikeajava"字元串生成對應的編碼資料,形式如下.1010100010111111110010001011111111001000101111111100100101001101110001110000011011101000111100101000101111111100110001001010011011100
3)思路:前面已經分析過了,而且我們講過了生成赫夫曼編碼的具體實作。
//為了調用友善,我們重載 getCodes
private static Map<Byte, String> getCodes(Node root) {
if(root == null) {
return null;
}
//處理root的左子樹
getCodes(root.left, "0", stringBuilder);
//處理root的右子樹
getCodes(root.right, "1", stringBuilder);
return huffmanCodes;
}
/**
* 功能:将傳入的node結點的所有葉子結點的赫夫曼編碼得到,并放入到huffmanCodes集合
* @param node 傳入結點
* @param code 路徑: 左子結點是 0, 右子結點 1
* @param stringBuilder 用于拼接路徑
*/
private static void getCodes(Node node, String code, StringBuilder stringBuilder) {
StringBuilder stringBuilder2 = new StringBuilder(stringBuilder);
//将code 加入到 stringBuilder2
stringBuilder2.append(code);
if(node != null) { //如果node == null不處理
//判斷目前node 是葉子結點還是非葉子結點
if(node.data == null) { //非葉子結點
//遞歸處理
//向左遞歸
getCodes(node.left, "0", stringBuilder2);
//向右遞歸
getCodes(node.right, "1", stringBuilder2);
} else { //說明是一個葉子結點
//就表示找到某個葉子結點的最後
huffmanCodes.put(node.data, stringBuilder2.toString());
}
}
}
最佳實踐-資料解壓(使用赫夫曼編碼解碼)
使用赫夫曼編碼來解碼資料,具體要求是
1)前面我們得到了赫夫曼編碼和對應的編碼byte[],即:[-88,-65,-56,-65,-56,-65,-55,77,-57,6,-24,-14,-117,-4,-60,-90,28]
2)現在要求使用赫夫曼編碼,進行解碼,又重新得到原來的字元串"ilikelikelikejavadoyoulikeajava"
3)思路:解碼過程,就是編碼的一個逆向操作
/**
* 将一個byte 轉成一個二進制的字元串, 如果看不懂,可以參考我講的Java基礎 二進制的原碼,反碼,補碼
* @param b 傳入的 byte
* @param flag 标志是否需要補高位如果是true ,表示需要補高位,如果是false表示不補, 如果是最後一個位元組,無需補高位
* @return 是該b 對應的二進制的字元串,(注意是按補碼傳回)
*/
private static String byteToBitString(boolean flag, byte b) {
//使用變量儲存 b
int temp = b; //将 b 轉成 int
//如果是正數我們還存在補高位
if(flag) {
temp |= 256; //按位與 256 1 0000 0000 | 0000 0001 => 1 0000 0001
}
String str = Integer.toBinaryString(temp); //傳回的是temp對應的二進制的補碼
if(flag) {
return str.substring(str.length() - 8);
} else {
return str;
}
}
//編寫一個方法,完成對壓縮資料的解碼
/**
*
* @param huffmanCodes 赫夫曼編碼表 map
* @param huffmanBytes 赫夫曼編碼得到的位元組數組
* @return 就是原來的字元串對應的數組
*/
private static byte[] decode(Map<Byte,String> huffmanCodes, byte[] huffmanBytes) {
//1. 先得到 huffmanBytes 對應的 二進制的字元串 , 形式 1010100010111...
StringBuilder stringBuilder = new StringBuilder();
//将byte數組轉成二進制的字元串
for(int i = 0; i < huffmanBytes.length; i++) {
byte b = huffmanBytes[i];
//判斷是不是最後一個位元組
boolean flag = (i == huffmanBytes.length - 1);
stringBuilder.append(byteToBitString(!flag, b));
}
//把字元串安裝指定的赫夫曼編碼進行解碼
//把赫夫曼編碼表進行調換,因為反向查詢 a->100 100->a
Map<String, Byte> map = new HashMap<String,Byte>();
for(Map.Entry<Byte, String> entry: huffmanCodes.entrySet()) {
map.put(entry.getValue(), entry.getKey());
}
//建立要給集合,存放byte
List<Byte> list = new ArrayList<>();
//i 可以了解成就是索引,掃描 stringBuilder
for(int i = 0; i < stringBuilder.length(); ) {
int count = 1; // 小的計數器
boolean flag = true;
Byte b = null;
while(flag) {
//1010100010111...
//遞增的取出 key 1
String key = stringBuilder.substring(i, i+count);//i 不動,讓count移動,指定比對到一個字元
b = map.get(key);
if(b == null) {//說明沒有比對到
count++;
}else {
//比對到
flag = false;
}
}
list.add(b);
i += count;//i 直接移動到 count
}
//當for循環結束後,我們list中就存放了所有的字元 "i like like like java do you like a java"
//把list 中的資料放入到byte[] 并傳回
byte b[] = new byte[list.size()];
for(int i = 0;i < b.length; i++) {
b[i] = list.get(i);
}
return b;
}
最佳實踐-檔案壓縮
我們學習了通過赫夫曼編碼對一個字元串進行編碼和解碼,下面我們來完成對檔案的壓縮和解壓,具體要求:給你一個圖檔檔案,要求對其進行無損壓縮,看看壓縮效果如何。
思路:讀取檔案->得到赫夫曼編碼表->完成壓縮
//編寫方法,将一個檔案進行壓縮
/**
*
* @param srcFile 你傳入的希望壓縮的檔案的全路徑
* @param dstFile 我們壓縮後将壓縮檔案放到哪個目錄
*/
public static void zipFile(String srcFile, String dstFile) {
//建立輸出流
OutputStream os = null;
ObjectOutputStream oos = null;
//建立檔案的輸入流
FileInputStream is = null;
try {
//建立檔案的輸入流
is = new FileInputStream(srcFile);
//建立一個和源檔案大小一樣的byte[]
byte[] b = new byte[is.available()];
//讀取檔案
is.read(b);
//直接對源檔案壓縮
byte[] huffmanBytes = huffmanZip(b);
//建立檔案的輸出流, 存放壓縮檔案
os = new FileOutputStream(dstFile);
//建立一個和檔案輸出流關聯的ObjectOutputStream
oos = new ObjectOutputStream(os);
//把 赫夫曼編碼後的位元組數組寫入壓縮檔案
oos.writeObject(huffmanBytes); //我們是把
//這裡我們以對象流的方式寫入 赫夫曼編碼,是為了以後我們恢複源檔案時使用
//注意一定要把赫夫曼編碼 寫入壓縮檔案
oos.writeObject(huffmanCodes);
}catch (Exception e) {
// TODO: handle exception
System.out.println(e.getMessage());
}finally {
try {
is.close();
oos.close();
os.close();
}catch (Exception e) {
// TODO: handle exception
System.out.println(e.getMessage());
}
}
}
最佳實踐-檔案解壓(檔案恢複)
具體要求:将前面壓縮的檔案,重新恢複成原來的檔案。
思路:讀取壓縮檔案(資料和赫夫曼編碼表)->完成解壓(檔案恢複
//編寫一個方法,完成對壓縮檔案的解壓
/**
*
* @param zipFile 準備解壓的檔案
* @param dstFile 将檔案解壓到哪個路徑
*/
public static void unZipFile(String zipFile, String dstFile) {
//定義檔案輸入流
InputStream is = null;
//定義一個對象輸入流
ObjectInputStream ois = null;
//定義檔案的輸出流
OutputStream os = null;
try {
//建立檔案輸入流
is = new FileInputStream(zipFile);
//建立一個和 is關聯的對象輸入流
ois = new ObjectInputStream(is);
//讀取byte數組 huffmanBytes
byte[] huffmanBytes = (byte[])ois.readObject();
//讀取赫夫曼編碼表
Map<Byte,String> huffmanCodes = (Map<Byte,String>)ois.readObject();
//解碼
byte[] bytes = decode(huffmanCodes, huffmanBytes);
//将bytes 數組寫入到目标檔案
os = new FileOutputStream(dstFile);
//寫資料到 dstFile 檔案
os.write(bytes);
} catch (Exception e) {
// TODO: handle exception
System.out.println(e.getMessage());
} finally {
try {
os.close();
ois.close();
is.close();
} catch (Exception e2) {
// TODO: handle exception
System.out.println(e2.getMessage());
}
}
}
赫夫曼編碼壓縮檔案注意事項
1)如果檔案本身就是經過壓縮處理的,那麼使用赫夫曼編碼再壓縮效率不會有明顯變化,比如視訊,ppt等等檔案[舉例壓一個.ppt]
2)赫夫曼編碼是按位元組來處理的,是以可以處理所有的檔案(二進制檔案、文本檔案)[舉例壓一個.xml檔案]
3)如果一個檔案中的内容,重複的資料不多,壓縮效果也不會很明顯
二叉排序樹
使用數組 數組未排序,優點:直接在數組尾添加,速度快。缺點:查找速度慢.
數組排序,優點:可以使用二分查找,查找速度快,缺點:為了保證數組有序,在添加新資料時,找到插入位置後,後面的資料需整體移動,速度慢。
使用鍊式存儲-連結清單
不管連結清單是否有序,查找速度都慢,添加資料速度比數組快,不需要資料整體移動。
使用二叉排序樹
二叉排序樹介紹
二叉排序樹:BST:(BinarySort(Search)Tree),對于二叉排序樹的任何一個非葉子節點,要求左子節點的值比目前節點的值小,右子節點的值比目前節點的值大。
特别說明:如果有相同的值,可以将該節點放在左子節點或右子節點
二叉排序樹建立和周遊
一個數組建立成對應的二叉排序樹,并使用中序周遊二叉排序樹,比如:數組為Array(7,3,10,12,5,1,9),建立成對應的二叉排序樹為:
二叉排序樹的删除
二叉排序樹的删除情況比較複雜,有下面三種情況需要考慮
1)删除葉子節點(比如:2,5,9,12)
2)删除隻有一顆子樹的節點(比如:1)
3)删除有兩顆子樹的節點.(比如:7,3,10)
4)操作的思路分析
第一種情況:
删除葉子節點 (比如:2, 5, 9, 12)
思路
(1) 需求先去找到要删除的結點 targetNode
(2) 找到targetNode 的 父結點 parent
(3) 确定 targetNode 是 parent的左子結點 還是右子結點
(4) 根據前面的情況來對應删除
左子結點 parent.left = null
右子結點 parent.right = null;
第二種情況: 删除隻有一顆子樹的節點 比如 1
思路
(1) 需求先去找到要删除的結點 targetNode
(2) 找到targetNode 的 父結點 parent
(3) 确定targetNode 的子結點是左子結點還是右子結點
(4) targetNode 是 parent 的左子結點還是右子結點
(5) 如果targetNode 有左子結點
\5. 1 如果 targetNode 是 parent 的左子結點
parent.left = targetNode.left;
5.2 如果 targetNode 是 parent 的右子結點
parent.right = targetNode.left;
(6) 如果targetNode 有右子結點
6.1 如果 targetNode 是 parent 的左子結點
parent.left = targetNode.right;
6.2 如果 targetNode 是 parent 的右子結點
parent.right = targetNode.right
情況三 : 删除有兩顆子樹的節點. (比如:7, 3,10 )
思路
(1) 需求先去找到要删除的結點 targetNode
(2) 找到targetNode 的 父結點 parent
(3) 從targetNode 的右子樹找到最小的結點
(4) 用一個臨時變量,将 最小結點的值儲存 temp = 11
(5) 删除該最小結點
(6) targetNode.value = temp
代碼實作:
package com.atguigu.binarysorttree;
public class BinarySortTreeDemo {
public static void main(String[] args) {
int[] arr = {7, 3};
BinarySortTree binarySortTree = new BinarySortTree();
//循環的添加結點到二叉排序樹
for(int i = 0; i< arr.length; i++) {
binarySortTree.add(new Node(arr[i]));
}
//中序周遊二叉排序樹
System.out.println("中序周遊二叉排序樹~");
binarySortTree.infixOrder(); // 1, 3, 5, 7, 9, 10, 12
//測試一下删除葉子結點
// binarySortTree.delNode(2);
// binarySortTree.delNode(1);
binarySortTree.delNode(3);
System.out.println("root=" + binarySortTree.getRoot());
System.out.println("删除結點後");
binarySortTree.infixOrder();
}
}
//建立二叉排序樹
class BinarySortTree {
private Node root;
public Node getRoot() {
return root;
}
//查找要删除的結點
public Node search(int value) {
if(root == null) {
return null;
} else {
return root.search(value);
}
}
//查找父結點
public Node searchParent(int value) {
if(root == null) {
return null;
} else {
return root.searchParent(value);
}
}
//編寫方法:
//1. 傳回的 以node 為根結點的二叉排序樹的最小結點的值
//2. 删除node 為根結點的二叉排序樹的最小結點
/**
*
* @param node 傳入的結點(當做二叉排序樹的根結點)
* @return 傳回的 以node 為根結點的二叉排序樹的最小結點的值
*/
public int delRightTreeMin(Node node) {
Node target = node;
//循環的查找左子節點,就會找到最小值
while(target.left != null) {
target = target.left;
}
//這時 target就指向了最小結點
//删除最小結點
delNode(target.value);
return target.value;
}
//删除結點
public void delNode(int value) {
if(root == null) {
return;
}else {
//1.需求先去找到要删除的結點 targetNode
Node targetNode = search(value);
//如果沒有找到要删除的結點
if(targetNode == null) {
return;
}
//如果我們發現目前這顆二叉排序樹隻有一個結點
if(root.left == null && root.right == null) {
root = null;
return;
}
//去找到targetNode的父結點
Node parent = searchParent(value);
//如果要删除的結點是葉子結點
if(targetNode.left == null && targetNode.right == null) {
//判斷targetNode 是父結點的左子結點,還是右子結點
if(parent.left != null && parent.left.value == value) { //是左子結點
parent.left = null;
} else if (parent.right != null && parent.right.value == value) {//是由子結點
parent.right = null;
}
} else if (targetNode.left != null && targetNode.right != null) { //删除有兩顆子樹的節點
int minVal = delRightTreeMin(targetNode.right);
targetNode.value = minVal;
} else { // 删除隻有一顆子樹的結點
//如果要删除的結點有左子結點
if(targetNode.left != null) {
if(parent != null) {
//如果 targetNode 是 parent 的左子結點
if(parent.left.value == value) {
parent.left = targetNode.left;
} else { // targetNode 是 parent 的右子結點
parent.right = targetNode.left;
}
} else {
root = targetNode.left;
}
} else { //如果要删除的結點有右子結點
if(parent != null) {
//如果 targetNode 是 parent 的左子結點
if(parent.left.value == value) {
parent.left = targetNode.right;
} else { //如果 targetNode 是 parent 的右子結點
parent.right = targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
}
//添加結點的方法
public void add(Node node) {
if(root == null) {
root = node;//如果root為空則直接讓root指向node
} else {
root.add(node);
}
}
//中序周遊
public void infixOrder() {
if(root != null) {
root.infixOrder();
} else {
System.out.println("二叉排序樹為空,不能周遊");
}
}
}
//建立Node結點
class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
//查找要删除的結點
/**
*
* @param value 希望删除的結點的值
* @return 如果找到傳回該結點,否則傳回null
*/
public Node search(int value) {
if(value == this.value) { //找到就是該結點
return this;
} else if(value < this.value) {//如果查找的值小于目前結點,向左子樹遞歸查找
//如果左子結點為空
if(this.left == null) {
return null;
}
return this.left.search(value);
} else { //如果查找的值不小于目前結點,向右子樹遞歸查找
if(this.right == null) {
return null;
}
return this.right.search(value);
}
}
//查找要删除結點的父結點
/**
*
* @param value 要找到的結點的值
* @return 傳回的是要删除的結點的父結點,如果沒有就傳回null
*/
public Node searchParent(int value) {
//如果目前結點就是要删除的結點的父結點,就傳回
if((this.left != null && this.left.value == value) ||
(this.right != null && this.right.value == value)) {
return this;
} else {
//如果查找的值小于目前結點的值, 并且目前結點的左子結點不為空
if(value < this.value && this.left != null) {
return this.left.searchParent(value); //向左子樹遞歸查找
} else if (value >= this.value && this.right != null) {
return this.right.searchParent(value); //向右子樹遞歸查找
} else {
return null; // 沒有找到父結點
}
}
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
//添加結點的方法
//遞歸的形式添加結點,注意需要滿足二叉排序樹的要求
public void add(Node node) {
if(node == null) {
return;
}
//判斷傳入的結點的值,和目前子樹的根結點的值關系
if(node.value < this.value) {
//如果目前結點左子結點為null
if(this.left == null) {
this.left = node;
} else {
//遞歸的向左子樹添加
this.left.add(node);
}
} else { //添加的結點的值大于 目前結點的值
if(this.right == null) {
this.right = node;
} else {
//遞歸的向右子樹添加
this.right.add(node);
}
}
}
//中序周遊
public void infixOrder() {
if(this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if(this.right != null) {
this.right.infixOrder();
}
}
}
平衡二叉樹(AVL樹)
基本介紹
1)平衡二叉樹也叫平衡二叉搜尋樹(Self-balancingbinarysearchtree)又被稱為AVL樹,可以保證查詢效率較高。
2)具有以下特點:它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1,并且左右兩個子樹都是一棵平衡二叉樹。平衡二叉樹的常用實作方法有紅黑樹、AVL、替罪羊樹、Treap、伸展樹等。
3)舉例說明,看看下面哪些AVL樹,為什麼?
應用案例-單旋轉(左旋轉 )
要求:給你一個數列,建立出對應的平衡二叉樹.數列{4,3,6,5,7,8}
思路分析
代碼實作
//左旋轉方法
private void leftRotate() {
//建立新的結點,以目前根結點的值
Node newNode = new Node(value);
//把新的結點的左子樹設定成目前結點的左子樹
newNode.left = left;
//把新的結點的右子樹設定成帶你過去結點的右子樹的左子樹
newNode.right = right.left;
//把目前結點的值替換成右子結點的值
value = right.value;
//把目前結點的右子樹設定成目前結點右子樹的右子樹
right = right.right;
//把目前結點的左子樹(左子結點)設定成新的結點
left = newNode;
}
應用案例-單旋轉(右旋轉)
要求:給你一個數列,建立出對應的平衡二叉樹.數列{10,12,8,9,7,6}
思路分析
代碼
//右旋轉
private void rightRotate() {
Node newNode = new Node(value);
newNode.right = right;
newNode.left = left.right;
value = left.value;
left = left.left;
right = newNode;
}
雙旋轉
前面的兩個數列,進行單旋轉(即一次旋轉)就可以将非平衡二叉樹轉成平衡二叉樹,但是在某些情況下,單旋轉不能完成平衡二叉樹的轉換。比如數列
int[] arr = { 10, 11, 7, 6, 8, 9 }; 運作原來的代碼可以看到,并沒有轉成 AVL樹
int[] arr = {2,1,6,5,7,3}; // 運作原來的代碼可以看到,并沒有轉成AVL樹
// 添加結點的方法
// 遞歸的形式添加結點,注意需要滿足二叉排序樹的要求
public void add(Node node) {
if (node == null) {
return;
}
// 判斷傳入的結點的值,和目前子樹的根結點的值關系
if (node.value < this.value) {
// 如果目前結點左子結點為null
if (this.left == null) {
this.left = node;
} else {
// 遞歸的向左子樹添加
this.left.add(node);
}
} else { // 添加的結點的值大于 目前結點的值
if (this.right == null) {
this.right = node;
} else {
// 遞歸的向右子樹添加
this.right.add(node);
}
}
//當添加完一個結點後,如果: (右子樹的高度-左子樹的高度) > 1 , 左旋轉
if(rightHeight() - leftHeight() > 1) {
//如果它的右子樹的左子樹的高度大于它的右子樹的右子樹的高度
if(right != null && right.leftHeight() > right.rightHeight()) {
//先對右子結點進行右旋轉
right.rightRotate();
//然後在對目前結點進行左旋轉
leftRotate(); //左旋轉..
} else {
//直接進行左旋轉即可
leftRotate();
}
return ; //必須要!!!
}
//當添加完一個結點後,如果 (左子樹的高度 - 右子樹的高度) > 1, 右旋轉
if(leftHeight() - rightHeight() > 1) {
//如果它的左子樹的右子樹高度大于它的左子樹的高度
if(left != null && left.rightHeight() > left.leftHeight()) {
//先對目前結點的左結點(左子樹)->左旋轉
left.leftRotate();
//再對目前結點進行右旋轉
rightRotate();
} else {
//直接進行右旋轉即可
rightRotate();
}
}
}
多路查找樹
二叉樹與B樹
二叉樹的操作效率較高,但是也存在問題,請看下面的二叉樹
1)二叉樹需要加載到記憶體的,如果二叉樹的節點少,沒有什麼問題,但是如果二叉樹的節點很多(比如1億),就存在如下問題:
2)問題1:在建構二叉樹時,需要多次進行i/o操作(海量資料存在資料庫或檔案中),節點海量,建構二叉樹時,速度有影響
3)問題2:節點海量,也會造成二叉樹的高度很大,會降低操作速度
多叉樹
1)在二叉樹中,每個節點有資料項,最多有兩個子節點。如果允許每個節點可以有更多的資料項和更多的子節點,就是多叉樹(multiwaytree)
2)後面我們講解的2-3樹,2-3-4樹就是多叉樹,多叉樹通過重新組織節點,減少樹的高度,能對二叉樹進行優化。3)舉例說明(下面2-3樹就是一顆多叉樹)
B樹的基本介紹
B樹通過重新組織節點,降低樹的高度,并且減少i/o讀寫次數來提升效率。
1)如圖B樹通過重新組織節點,降低了樹的高度.
2)檔案系統及資料庫系統的設計者利用了磁盤預讀原理,将一個節點的大小設為等于一個頁(頁得大小通常為4k),這樣每個節點隻需要一次I/O就可以完全載入
3)将樹的度M設定為1024,在600億個元素中最多隻需要4次I/O操作就可以讀取到想要的元素,B樹(B+)廣泛應用于檔案存儲系統以及資料庫系統中
2-3樹
2-3樹是最簡單的B樹結構,具有如下特點:
1)2-3樹的所有葉子節點都在同一層.(隻要是B樹都滿足這個條件)
2)有兩個子節點的節點叫二節點,二節點要麼沒有子節點,要麼有兩個子節點.
3)有三個子節點的節點叫三節點,三節點要麼沒有子節點,要麼有三個子節點.
4)2-3樹是由二節點和三節點構成的樹。
2-3樹應用案例
将數列{16,24,12,32,14,26,34,10,8,28,38,20}建構成2-3樹,并保證資料插入的大小順序。(示範一下建構2-3樹的過程.)
插入規則:
1)2-3樹的所有葉子節點都在同一層.(隻要是B樹都滿足這個條件)
2)有兩個子節點的節點叫二節點,二節點要麼沒有子節點,要麼有兩個子節點.
3)有三個子節點的節點叫三節點,三節點要麼沒有子節點,要麼有三個子節點
4)當按照規則插入一個數到某個節點時,不能滿足上面三個要求,就需要拆,先向上拆,如果上層滿,則拆本層,拆後仍然需要滿足上面3個條件。
5)對于三節點的子樹的值大小仍然遵守(BST二叉排序樹)的規則
B樹、B+樹和B*樹
B樹的介紹
B-tree樹即B樹,B即Balanced,平衡的意思。有人把B-tree翻譯成B-樹,容易讓人産生誤解。會以為B-樹是一種樹,而B樹又是另一種樹。實際上,B-tree就是指的B樹。
前面已經介紹了2-3樹和2-3-4樹,他們就是B樹(英語:B-tree也寫成B-樹),這裡我們再做一個說明,我們在學習Mysql時,經常聽到說某種類型的索引是基于B樹或者B+樹的,如圖:
對上圖的說明:
1)B樹的階:節點的最多子節點個數。比如2-3樹的階是3,2-3-4樹的階是4
2)B-樹的搜尋,從根結點開始,對結點内的關鍵字(有序)序列進行二分查找,如果命中則結束,否則進入查詢關鍵字所屬範圍的兒子結點;重複,直到所對應的兒子指針為空,或已經是葉子結點
3)關鍵字集合分布在整顆樹中,即葉子節點和非葉子節點都存放資料.
4)搜尋有可能在非葉子結點結束
5)其搜尋性能等價于在關鍵字全集内做一次二分查找
B+樹的介紹
B+樹是B樹的變體,也是一種多路搜尋樹。
對上圖的說明:
1)B+樹的搜尋與B樹也基本相同,差別是B+樹隻有達到葉子結點才命中(B樹可以在非葉子結點命中),其性能也等價于在關鍵字全集做一次二分查找
2)所有關鍵字都出現在葉子結點的連結清單中(即資料隻能在葉子節點【也叫稠密索引】),且連結清單中的關鍵字(資料)恰好是有序的。
3)不可能在非葉子結點命中
4)非葉子結點相當于是葉子結點的索引(稀疏索引),葉子結點相當于是存儲(關鍵字)資料的資料層
5)更适合檔案索引系統
6)B樹和B+樹各有自己的應用場景,不能說B+樹完全比B樹好,反之亦然
B*樹的介紹
B*樹是B+樹的變體,在B+樹的非根和非葉子結點再增加指向兄弟的指針。
1)B*樹定義了非葉子結點關鍵字個數至少為(2/3)M,即塊的最低使用率為2/3,而B+樹的塊的最低使用率為的1/2。2)從第1個特點我們可以看出,B樹配置設定新結點的機率比B+樹要低,空間使用率更高