SGU 298. King Berl VI
Time limit per test: 1.5 second(s)
Memory limit: 65536 kilobytes input: standard
output: standard
King Berl VI has N daughters and no sons. During his long life he gave a number of promises to his daughters. All the promises have the following wording: "daughter Xi, I promise to give you dowry not less than Ci burles more than to daughter Yi", where i represents the number of the promise. Before his death the king decided to give some amount of money to each daughter. As far as he was the fair king, he decided to fullfill all his promises. But he was not only fair but also very greedy, he decided that he can give negative amount of burles as a dowry (i.e. daughter should pay this amount of burles to the treasury). Because of his born greed and by advice of the minister of finances, he made a decision that absolute value of each dowry should not exceed 10000 burles and the difference between dowry of the oldest and of the youngest daughters should be as small as possible (note, this value can be negative).
I.e. if the dowry given to the i-th daughter is Ai, folllowing conditions should be satisfied:
- -10000≤ Ai≤ 10000
- AN - A1 should be minimal
Input
The fist line of the input file contains two integers numbers N and M (2≤ N≤ 10000; 0≤ M≤ 100000), where N is the number of daughters and M is the number of promises. The following M lines contain the description of promises in the following form: Xi, Yi, Ci (1≤ Xi, Yi≤ N; Xi≠ Yi; 0≤ Ci≤ 1000). The youngest daughter has the number one, the oldest — N. Each pair Xi, Yi can appear in the input several times.
Output
Write to the output number -1 if there is no solution for the problem (i.e. there is no sequence of N integers which satisfies all described above requirements). Write to the output N integer numbers — the amount of dowry of each daughter in burles, if solution exists. If there are several solutions output any of them.
Example(s)
| |
| |
| |
| |
************************************************
題目大意:一個國王給他的n的女兒有m個承諾:a女兒的嫁妝比b女兒的嫁妝多c元或者等于c元。女兒的嫁妝可以是負數。一個女兒的嫁妝的絕對值比10000小。現在要求第n個女兒減去第1個女兒的值最小,求出序列。
解題思路:蛋疼地苦思冥想了2的成果也是對差分限制的深刻了解了吧:
差分限制系統
差分限制的一類求最大最小值,一般都說用最短路求最大值,用最長路求最小值。一種有點YY的證明,就拿最短路求最大值來說,一般最短路的時候初始值都是指派為inf的,然後這個最短路不斷更新也就是頂點的值不斷減小,一旦更新到了最大一組解的時候,這個時候已經滿足所有邊的要求了,此時就不會再更新了,是以,最短路求出來的是最大解。比較YY的證明,總比沒有好,就這樣了解吧。
有一個定死的源點是有好處的。一個定死的源點的初始值是val,連到各個點的邊的權值為0:
在用最短路求的時候,一開始所有點的初始值為inf,而最終求出的解是所有裡面的最大值,并且,所有的值都比val小; 在用最長路求的時候,一開始所有的點初始值為-inf,而最終求出的解是所有裡面的最小值,并且,所有的值都比val大。這樣以來,如果一個差分限制系統的解有規定的上界uplim,我們可以外加一個源點,給它的初始值是uplim,然後從這個源點連到所有點的邊權值為0,再用最短路求,求出的解的值必定比uplim小,而且是最大解,換句話說最靠近uplim的解。反之,如果一個差分限制系統的解有規定的下界downlim,我們可以外加一個源點,給它的初始值是downlim,然後從這個源點連到所有點的邊權值為0,再用最長路求,求出的解的值必定比downlim大,而且是最小解,也就是最靠近downlim的解。
假設,一個差分限制系統有3個限制條件:a-b>=1,a-c>=2,c-b>=3,如果我們要求出a,b,c不比0大且最靠近0的那組解,我們就會建立如下的差分限制圖:
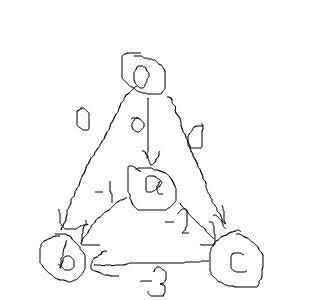
然後做最短路求最大解,求出了一組解{a,b,c}={0,-5,-2},但如果我們現在要求的是a,b,c都不比0大的且最靠近0的那組解,我們會建立這樣的差分限制圖:
可見除了源點連出去的邊不變外,其他邊的方向取反,大小變成相反數。然後我們做最長路求最小解,可以得到{a,b,c}={5,0,3},有點覺得怪異了:上面兩組解的結構是一樣的,他們互相之間都隻差了一個常數。然而,這個不是偶然,可以小證明一下:一個差分限制系統,先不考慮源點的問題,如果a有一條路徑L連到b,這個路徑是從a到b的最短路,a還可以通過其他途徑連到b,那麼當所有邊都取反,權值也取相反數,從b到a通過路徑L一定是最長路。那麼換句話說也就是a一開始被什麼東西制約,他後來還是被那個東西制約。是以第一次用正向邊正權(這個正權的含義是相對與權值取相反數之後的反權來說的)做最短路求出來解一定和第二次用反向邊反權做最長路求出來的解一定是結構相同都隻是差了一個k的值。這個結論的意義是:如果差分限制的點的被限定了上下界,我們可以用一次最短路一次最長路來算出的最靠近上界的一組解和最靠近下界的一組解結構相同,然後,所有的解取值範圍就一定在這兩個解的值之間,不可能出現有一個解中一個點的取值超過這兩組解的範圍的。
還有一個連等式:(規定求最短路的那個圖為正向邊和正權)正向邊正權最短路的解的結構=反向邊反權最長路解的結構=正向邊反權最長路解的值取相反數之後的結構=反向邊正權最短路解的值取相反數之後的結構。前兩個已經證明,第一個和第三個也很好證明:原來的最短路,取了相反數之後肯定變成最長路了,然而值也變成了相反數關系。并且,第一個和第三個的解是相反數,第二個和第四個解是相反數。
在一個差分限制系統中,如果之前已經做完最短路,現在把一個解xi給人為地縮小,然後再重新做最短路,這個是可以的。因為xi縮小,那麼所有指向vi的邊都還是能滿足dis[v]<=dis[u]+cost的,但是vi出去的邊就不能滿足上面那個不等式了,然後,重新spfa能更新vi點以後的所有滿足的點。但是如果做完最短路後把一個點人為擴大,我覺得這是不允許的,因為所有指向vi的邊就不滿足不等式了,重新spfa 的話應該不會有任何結果,因為vi指出去的邊都滿足,而指進來的邊不會更新到,這樣就搞笑了。與此同理,做完最長路後,我們可以把一個點人為地放大,然後spfa,但是不能縮小。
下面貼代碼(研究透了_LT_zyc的代碼http://hi.baidu.com/_lt_zyc/item/554a4f1979f311536826bb53):
//#pragma comment(linker, "/STACK:65536000")
#include <map>
#include <stack>
#include <queue>
#include <math.h>
#include <vector>
#include <string>
#include <fstream>
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>
#define N 10005
#define M 200005
#define E
#define inf 0x3f3f3f3f
#define dinf 1e10
#define linf (LL)1<<60
#define LL long long
#define clr(a,b) memset(a,b,sizeof(a))
using namespace std;
const int lim = 10000;
int n,m,eid;
int head[N],ed[M],nxt[M],val[M];
int x[M],y[M],v[M];
int d1[N],d2[N],vis[N],num[N];
queue<int>que;
void addedge(int s,int e,int v)
{
ed[eid]=e;val[eid]=v;
nxt[eid]=head[s];head[s]=eid++;
}
int spfa(int d[])
{
while(!que.empty())
{
int s=que.front();que.pop();
vis[s]=0;
for(int i=head[s];~i;i=nxt[i])
{
int e=ed[i],v=val[i];
if(d[e]>d[s]+v)
{
d[e]=d[s]+v;
if(!vis[e])
{
if(num[e]>n)return -1;
num[e]++;vis[e]=1;
que.push(e);
}
}
}
}
return 1;
}
int main()
{
//freopen("/home/axorb/in","r",stdin);
scanf("%d%d",&n,&m);
for(int i=0;i<m;i++)
scanf("%d%d%d",&x[i],&y[i],&v[i]);
eid=0;clr(head,-1);
for(int i=0;i<m;i++)addedge(x[i],y[i],-v[i]);
clr(vis,0);clr(num,0);
while(!que.empty())que.pop();
for(int i=1;i<=n;i++){d1[i]=0;que.push(i);}
int k=spfa(d1);
if(k==-1){puts("-1");return 0;}
for(int i=1;i<=n;i++)d1[i]+=lim;
eid=0;clr(head,-1);
for(int i=0;i<m;i++)addedge(y[i],x[i],-v[i]);
clr(vis,0);clr(num,0);
while(!que.empty())que.pop();
for(int i=1;i<=n;i++){d2[i]=0;que.push(i);}
k=spfa(d2);
if(k==-1){puts("-1");return 0;}
for(int i=1;i<=n;i++)d2[i]=-d2[i]-lim;
// for(int i=1;i<=n;i++)
// printf("%d: %d %d\n",i,d1[i],d2[i]);
for(int i=1;i<=n;i++)
if(d2[i]>d1[i]){puts("-1");return 0;}
eid=0;clr(head,-1);
for(int i=0;i<m;i++)addedge(x[i],y[i],-v[i]);
clr(vis,0);clr(num,0);
while(!que.empty())que.pop();
d1[n]=d2[n];que.push(n);
spfa(d1);
for(int i=1;i<=n;i++)
if(i==n)printf("%d\n",d1[i]);
else printf("%d ",d1[i]);
return 0;
}
轉載于:https://www.cnblogs.com/Fatedayt/archive/2012/05/24/2517160.html