1 focal loss的概述
焦點損失函數 Focal Loss(2017年何凱明大佬的論文)被提出用于密集物體檢測任務。
當然,在目标檢測中,可能待檢測物體有1000個類别,然而你想要識别出來的物體,隻是其中的某一個類别,這樣其實就是一個樣本非常不均衡的一個分類問題。
而Focal Loss簡單的說,就是解決樣本數量極度不平衡的問題的。
說到樣本不平衡的解決方案,想必大家是知道一個混淆矩陣的f1-score的,但是這個好像不能用在訓練中當成損失。而Focal loss可以在訓練中,讓小數量的目标類别增權重重,讓分類錯誤的樣本增權重重。
先來看一下簡單的二值交叉熵的損失:
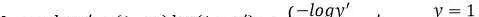
- y’是模型給出的預測類别機率,y是真實樣本。就是說,如果一個樣本的真實類别是1,預測機率是0.9,那麼
-log(0.9)
就是這個損失。
- 講道理,一般我不喜歡用二值交叉熵做例子,用多分類交叉熵做例子會更舒服。
【然後看focal loss的改進】:
這個增加了一個
(1-y')^\gamma
的權重值,怎麼了解呢?就是如果給出的正确類别的機率越大,那麼
(1-y')^\gamma
就會越小,說明分類正确的樣本的損失權重小,反之,分類錯誤的樣本的損權重大。
【focal loss的進一步改進】:
這裡增加了一個
\alpha
,這個alpha在論文中給出的是0.25,這個就是單純的降低正樣本或者負樣本的權重,來解決樣本不均衡的問題。
兩者結合起來,就是一個可以解決樣本不平衡問題的損失focal loss。
【總結】:
\alpha
解決了樣本的不平衡問題;
\beta
解決了難易樣本不平衡的問題。讓樣本更重視難樣本,忽視易樣本。
- 總之,Focal loss會的關注順序為:樣本少的、難分類的;樣本多的、難分類的;樣本少的,易分類的;樣本多的,易分類的。
2 GHM
- GHM是Gradient Harmonizing Mechanism。
這個GHM是為了解決Focal loss存在的一些問題。
【Focal Loss的弊端1】讓模型過多的關注特别難分類的樣本是會有問題的。樣本中有一些異常點、離群點(outliers)。是以模型為了拟合這些非常難拟合的離群點,就會存在過拟合的風險。
2.1 GHM的辦法
Focal Loss是從置信度p的角度入手衰減loss的。而GHM是一定範圍内置信度p的樣本數量來衰減loss的。
首先定義了一個變量g,叫做梯度模長(gradient norm):
可以看出這個梯度模長,其實就是模型給出的置信度
p^*
與這個樣本真實的标簽之間的內插補點(距離)。g越小,說明預測越準,說明樣本越容易分類。
下圖中展示了g與樣本數量的關系:
【從圖中可以看到】
- 梯度模長接近于0的樣本多,也就是易分類樣本是非常多的
- 然後樣本數量随着梯度模長的增加迅速減少
- 然後當梯度模長接近1的時候,樣本的數量又開始增加。
GHM是這樣想的,對于梯度模長小的易分類樣本,我們忽視他們;但是focal loss過于關注難分類樣本了。關鍵是難分類樣本其實也有很多!,如果模型一直學習難分類樣本,那麼可能模型的精确度就會下降。是以GHM對于難分類樣本也有一個衰減。
那麼,GHM對易分類樣本和難分類樣本都衰減,那麼真正被關注的樣本,就是那些不難不易的樣本。而抑制的程度,可以根據樣本的數量來決定。
這裡定義一個GD,梯度密度:
GD(g)=\frac{1}{l(g)}\sum_{k=1}^N{\delta(g_k,g)}
GD(g)
是計算在梯度g位置的梯度密度;
\delta(g_k,g)
就是樣本k的梯度
g_k
是否在
[g-\frac{\epsilon}{2},g+\frac{\epsilon}{2}]
這個區間内。
l(g)
就是
[g-\frac{\epsilon}{2},g+\frac{\epsilon}{2}]
這個區間的長度,也就是
\epsilon
總之,
GD(g)
就是梯度模長在
[g-\frac{\epsilon}{2},g+\frac{\epsilon}{2}]
内的樣本總數除以
\epsilon
.
然後把每一個樣本的交叉熵損失除以他們對應的梯度密度就行了。
L_{GHM}=\sum^N_{i=1}{\frac{CE(p_i,p_i^*)}{GD(g_i)}}
CE(p_i,p_i^*)
表示第i個樣本的交叉熵損失;
GD(g_i)
表示第i個樣本的梯度密度;
2.2 論文中的GHM
論文中呢,是把梯度模長劃分成了10個區域,因為置信度p是從0~1的,是以梯度密度的區域長度就是0.1,比如是0~0.1為一個區域。
下圖是論文中給出的對比圖:
【從圖中可以得到】
- 綠色的表示交叉熵損失;
- 藍色的是focal loss的損失,發現梯度模長小的損失衰減很有效;
- 紅色是GHM的交叉熵損失,發現梯度模長在0附近和1附近存在明顯的衰減。
當然可以想到的是,GHM看起來是需要整個樣本的模型估計值,才能計算出梯度密度,才能進行更新。也就是說mini-batch看起來似乎不能用GHM。
在GHM原文中也提到了這個問題,如果光使用mini-batch的話,那麼很可能出現不均衡的情況。
【我個人覺得的處理方法】
- 可以使用上一個epoch的梯度密度,來作為這一個epoch來使用;
- 或者一開始先使用mini-batch計算梯度密度,然後模型收斂速度下降之後,再使用第一種方式進行更新。