Chapter2.1 -- 整數規劃(ILP)
By 進棧需檢票
一、前情提要
當題目要求的最優解是整數,例如物件的數量,參與人員的數量等時,就不能繼續使用之前的線性規劃了(當出現小數的情況),這個時候需考慮整數規劃這樣的一種模組化形式
但是目前所流行的求整數規劃的方法,隻适用于整數線性規劃,不能解決一切的整數規劃問題
分類:
1.變量全限制為整數時,稱為純(完全)整數規劃
2.變量部分限制為整數時,稱為混合整數規劃
整數規劃特點:
1.原線性規劃有最優解,當自變量限制為整數的時候:
(1)原線性規劃的最優解全為整數,則整數規劃的最優解與原線性規劃的最優解一緻
(2)整數規劃可能無解(考慮原先自變量的取值範圍)
$$
0 \leq x_1\leq 1 \ \ \ \ \ 0.1 \leq x_2 \leq 0.9
$$
這樣的情況下,考慮到自身自變量無法取整,最後的最優解不是整數就是肯定的
(3)有可行解(存在最優解),但是最優解值有變差(效果worse)
2.整數規劃的最優解==不能按照實數最優解簡單的取整去得到==
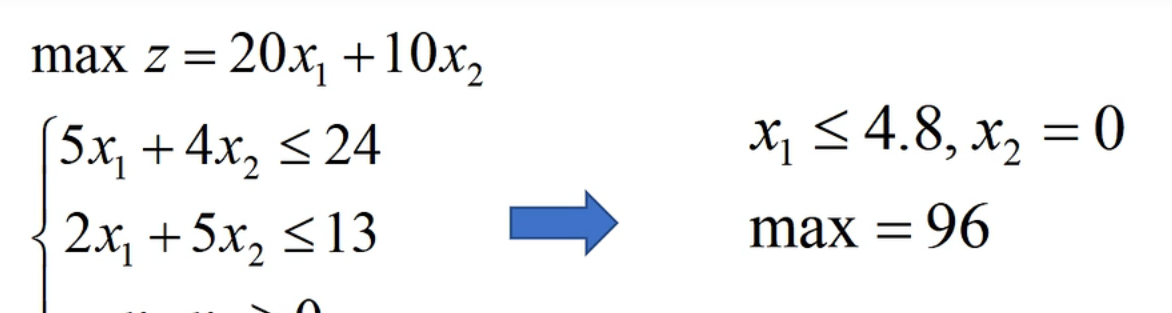
如此,如果簡單的把$x_1$約等為5,那麼第一個限制條件則無法完成
二、經典例子
1.初識
Example1 -- 下料
目标函數
$$
min\ Z = \sum_{j = 1}^nx_j
$$
限制條件
$$
\sum_{j = 1}^na_{ij}x_j\geq b_i\ \ (i = 1 , 2, L , n)
$$
$$
x_j \geq 0\ \ (j = 1 , 2 , L , n)
$$
Example2 -- 建廠
目标函數:
前半部分是運輸的總共費用,後半部分是建廠的費用(沒有建廠的$x_{ij} = 0$)
限制條件:
(1)運輸的量應該要小于總的生産能力
(2)同時運輸的量要滿足于運輸地的需求量
(3)定義取值限制
2.一般形式
其中$x_j$為考慮的整數
三、其他類型
1.1松弛變量
當題目中出現以下等式的時候(==小于等于一個整數==)
$$
x_1 + x_2 \leq 10
$$
此時不好去分析$x_1\ ,\ x_2$的整數情況
那麼此時引入臨時變量$x_3$
$$
x_1 + x_2 + x_3 = 10
$$
若
$$
x_3 \geq 0
$$
則必有
$$
x_1 + x_2 \leq 10
$$
那麼此時$x_1\ ,\ x_2$兩個變量的整數問題就轉化到了x3身上,x3就是所謂的松弛變量
1.2剩餘變量
與1.1類似,此時情況為==大于等于一個整數==
$$
x_1 + x_2 \geq 10
$$
$$
x_1+x_2-x_3 = 10
$$
$$
x_3 \geq 0
$$
隻要滿足$x_3$大于等于0,那麼$x_1 + x_2 \geq 10$就一定存在,在這裡,$x_3$就是所謂的剩餘變量
2.全整數規劃:
在這中情況下,所有的變量包括我們可能引入的松弛變量和剩餘變量都需要為整數的時候
3.混合整數規劃:
如名字所示
4. 0--1整數規劃(非黑即白)
所有的決策變量隻能去 $0 , 1$兩個整數(一般适用于工作安排,非黑即白)
四、整數規劃和線性規劃的關系
1.整數規劃可行解是松弛問題可行域中的整數網格點
2.松弛問題無可行解,整數規劃也不會有可行解
3.ILP最優質小于或等于松弛問題的最優解
4.松弛問題的最優解滿足整數條件,則該最優解可以作為整數規劃的最優解
五、算法1:分支定界算法
Example1
首先不考慮整數限制,得到一般的線性規劃問題
目标函數
$$
max\ Z = x_1+x_2
$$
限制條件
$$
14x_1 + 9x_2 \leq51
$$
$$
-6x_1+3x_2\leq 1
$$
$$
x_1\ ,x_2 \geq 0
$$
(一般稱之為松弛問題或者伴随問題)
法一:高中的圖解法
法二:分支定界法
假設$x_i^0 = 2.3$,則$[x_i^o] = 2$,也就是所謂的取整計算,通過分别的去構造新的兩個限制條件:
$$
x_i \leq [x_i^o] = 2
$$
$$
x_i \geq [x_i^o] + 1 = 3
$$
==注意==:一定記得是分别使用兩種限制條件!!
Example2
$$
max Z = 3x_1 + 2x_2 \
\begin{cases}
2x_1+3x_2 \leq 14\
2x_1+x_2 \leq 9\
x_1\ , x_2 \geq 0 \ \ 且為整數
\end{cases}
$$
松弛問題首先看待:
f = [-3 , -2];
A = [2 3;
2 1];
b = [14 , 9];
lb = [0 , 0];
ub = [inf , inf];
[x , fval] = linprog(f , A , b , [ ] , [ ] , lb , ub);
x
fval = -fval;
fval
----------
Output
x =
3.2500
2.5000
fval =
14.7500
此時均不是整數,采用分支定界算法
①$x_i^0 \leq [x_i^0]$
$$
max Z = 3x_1 + 2x_2 \
\begin{cases}
2x_1+3x_2 \leq 14\
2x_1+x_2 \leq 9\
x_1 \leq3 \
x_1\ , x_2 \geq 0 \ \ 且為整數
\end{cases}
$$
f = [-3 , -2];
A = [2 3;
2 1];
b = [14 , 9];
lb = [0 , 0];
ub = [3 , inf];
[x , fval] = linprog(f , A , b , [ ] , [ ] , lb , ub);
x
fval = -fval;
fval
----------
Output
x =
3.0000
2.6667
fval =
14.3333
此時任然不滿足整數的條件,繼續嘗試
②$x_i^0 \geq [x_i^0] + 1$
$$
max Z = 3x_1 + 2x_2 \
\begin{cases}
2x_1+3x_2 \leq 14\
2x_1+x_2 \leq 9\
x_1 \geq 4 \
x_1\ , x_2 \geq 0 \ \ 且為整數
\end{cases}
$$
f = [-3 , -2];
A = [2 3;
2 1];
b = [14 , 9];
lb = [4 , 0];
ub = [inf , inf];
[x , fval] = linprog(f , A , b , [ ] , [ ] , lb , ub);
x
fval = -fval;
fval
----------
Output
x =
4.0000
1.0000
fval =
14.0000
像啊,太像了,而且隻要決策變量為整數就行
==但是==,這個時候我們還不能确定,因為我們隻嘗試了$x_1$
③$x_2 \leq [x_2] = 2$
$$
max Z = 3x_1 + 2x_2 \
\begin{cases}
2x_1+3x_2 \leq 14\
2x_1+x_2 \leq 9\
x_2 \leq 2 \
x_1\ , x_2 \geq 0 \ \ 且為整數
\end{cases}
$$
f = [-3 , -2];
A = [2 3;
2 1];
b = [14 , 9];
lb = [0 , 0];
ub = [inf , 2];
[x , fval] = linprog(f , A , b , [ ] , [ ] , lb , ub);
x
fval = -fval;
fval
----------
Output
x =
3.5000
2.0000
fval =
14.5000
no
④$x_2 \geq [x_2]+1 = 3$
$$
max Z = 3x_1 + 2x_2 \
\begin{cases}
2x_1+3x_2 \leq 14\
2x_1+x_2 \leq 9\
x_2 \geq 3 \
x_1\ , x_2 \geq 0 \ \ 且為整數
\end{cases}
$$
f = [-3 , -2];
A = [2 3;
2 1];
b = [14 , 9];
lb = [0 , 3];
ub = [inf , inf];
[x , fval] = linprog(f , A , b , [ ] , [ ] , lb , ub);
x
fval = -fval;
fval
----------
Output
x =
2.5000
3.0000
fval =
13.5000
此時好像也沒有哦
==但是==,我們還有兩個決策變量一起的情況沒有與考慮
鑒于隻有第②種情況才是整數的,是以我們基于$x_1 \geq 4$來去思考$x_2$的範圍是否影響最後的值
⑤
$$
max Z = 3x_1 + 2x_2 \
\begin{cases}
2x_1+3x_2 \leq 14\
2x_1+x_2 \leq 9\
x_1 \geq 4 \ ,\ x_2 \leq 2\
x_1\ , x_2 \geq 0 \ \ 且為整數
\end{cases}
$$
f = [-3 , -2];
A = [2 3;
2 1];
b = [14 , 9];
lb = [4 , 0];
ub = [inf , 2];
[x , fval] = linprog(f , A , b , [ ] , [ ] , lb , ub);
x
fval = -fval;
fval
----------
Output
x =
4.0000
1.0000
fval =
14.0000
same
⑥
$$
max Z = 3x_1 + 2x_2 \
\begin{cases}
2x_1+3x_2 \leq 14\
2x_1+x_2 \leq 9\
x_1 \geq 4 \ ,\ x_2 \geq 3\
x_1\ , x_2 \geq 0 \ \ 且為整數
\end{cases}
$$
f = [-3 , -2];
A = [2 3;
2 1];
b = [14 , 9];
lb = [4 , 3];
ub = [inf , inf];
[x , fval] = linprog(f , A , b , [ ] , [ ] , lb , ub);
x
fval = -fval;
fval
----------
Output
Linprog stopped because no point satisfies the constraints.
當然,為了保險起見
⑦
$$
max Z = 3x_1 + 2x_2 \
\begin{cases}
2x_1+3x_2 \leq 14\
2x_1+x_2 \leq 9\
x_1 \leq 3 \ ,\ x_2 \geq 3\
x_1\ , x_2 \geq 0 \ \ 且為整數
\end{cases}
$$
x =
2.5000
3.0000
fval =
13.5000
no
⑧
$$
max Z = 3x_1 + 2x_2 \
\begin{cases}
2x_1+3x_2 \leq 14\
2x_1+x_2 \leq 9\
x_1 \leq 3 \ ,\ x_2 \leq 2\
x_1\ , x_2 \geq 0 \ \ 且為整數
\end{cases}
$$
x =
3
2
fval =
13
!,但是看來看去還是沒有第②種來得大
綜上所述,最大的情況為②
當然,增加了限制條件求出來的值肯定比沒增加之前來的差,是以,其實我們隻要分别考慮$x_1\ ,\ x_2$兩個決策變量的新的限制條件去分别限制求值就好了
intlinprog( )
intlinprog( )
在
linprog( )
的基礎上,基于整數的求解要求,發展出了
intlinprog( )
函數
x = intlinprog(f,intcon,A,b,Aeq,beq,lb,ub,x0,options)
[x,fval,exitflag,output] = intlinprog(...)
其格式标注如下
$$
min\ f^Tx\
\begin{cases}
x(intcon)\ are\ integers\
\textbf{A} \cdot x \leq b\
\textbf{Aeq} \cdot x = beq\
lb\leq x \leq ub
\end{cases}
$$
與
linprog
相比,多了參數
intcon
,代表了整數決策變量所在的位置
整數限制組成的向量,指定為正整數向量。
intcon
中的值訓示決策變量
x
中應取整數值的分量。
intcon
的值在
1
到
numel(f)
範圍内
intcon = [1,2,7]
表示
x(1)
、
x(2)
和
x(7)
僅取整數值
Example1 求解具有線性不等式的MILP
$$
min \ Z = 8x_1+x_2 \
\begin{cases}
x_2(intcon)\ are\ integers\
x_1+2x_2 \geq-14\
-4x_1-x_2 \leq -33\
2x_1+x_2 \leq20
\end{cases}
$$
f = [8 , 1];
intcon = 2;
A = [-1 , -2
-4 , -1
2 , 1];
b = [14 , -33 , 20];
[x , fval] = intlinprog(f,intcon,A,b);
x
fval
----------
Output
x =
6.5000
7.0000
fval =
59.0000
Example2
$$
max\ Z = 5x_1+8x_2\
\begin{cases}
x_1\ , \ x_2(intcon)\ are\ integers\
x_1+x_2\leq 6\
5x_1+9x_2\leq 45\
x_1\ ,\ x_2 \geq 0
\end{cases}
$$
f = [-5 , -8];
A = [1 1
5 9];
b = [6 , 45];
lb = zeros(2 , 1);
intcon=[1 , 2];
[x , fval] = intlinprog(f , intcon , A , b , [ ] , [ ] , lb , [ ]);
x
fval = -fval
----------
Output
x =
0
5.0000
fval =
40
Example3 0—1規劃
$$
max\ Z = 6x_1 + 2x_2 + 3x_3 + 5x_4\
\begin{cases}
3x_1 - 5x_2 + x_3 + 6x_4 \geq 4\
2x_1 + x_2 + x_3 - x_4 \leq 3\
x_1 + 2x_2 +4x_3 + 5x_4 \leq 10\
x_j=0\ or \ 1, \ \ j = 1\ ,2\ ,3\ ,4
\end{cases}
$$
f = [-6 , -2 , -3 , -5];
A=[-3 5 -1 -6
2 1 1 -1
1 2 4 5];
b=[-4 , 3 , 10];
intcon=[1 ,2 , 3 , 4];
lb = zeros(4 , 1);
ub = ones(4 , 1);
[x , fval] = intlinprog(f , intcon , A , b , [ ] , [ ] , lb , ub);
x
fval = -fval
----------
Ouptut
x =
1
0
1
1
fval =
14
當然,我們也可以使用Lingo這個軟體去實作以上功能
不在此次讨論範圍内
六、算法2:割平面算法(Branch-and-Cut 、Cutting Plane Method)
“本内容部分借鑒于:https://zhuanlan.zhihu.com/p/28387290”
1.基本原理
①如果松弛問題無解,則此題目也無解(通用)
②如果松弛問題的最優解就是整數,則也是割平面算法的最優解(通用)
③如果松弛問題(P0)無整數解,則對原始題目增加割平面條件:
a.對P0增加一個線性限制條件,将P0的可行區域割掉一小塊
b.使得整數解恰好落在割掉的那一部分,但又沒有割掉原問題的可行解
Example
$$
max\ Z = x_1 + x_2\
\begin{cases}
-x_1 + x_2 \leq 1\
3x_1 + x_2 \leq 4\
x_1\ ,\ x_2 \geq 0\
x_1\ ,\ x_2 \ are\ integers
\end{cases}
$$
% LP
f = [-1 , -1];
A = [-1 , 1
3 , 1];
b = [1 , 4];
lb = [0 , 0];
[x , fval] = linprog(f , A , b , [ ] , [ ] , lb);
x
fval = -fval
----------
Output
x =
0.7500
1.7500
fval =
2.5000
% ILP
f = [-1 , -1];
intcon = [1 , 2];
A = [-1 , 1
3 , 1];
b = [1 , 4];
lb = [0 , 0];
[x , fval] = intlinprog(f , intcon , A , b , [ ] , [ ] , lb);
x
fval = -fval
----------
Output
x =
1
1
fval =
2.0000
這就是以上兩種方法求出來的解
現在我們數形結合一下:
交點為(3/4 , 7/4),從這裡我們可以看到,$x_2 - 1\geq 0$以及$x_1-1\geq 0$這兩個區域,割掉并不會影響到最後的取值
是以最後隻保留那個正方形區域,易得解
2.使用方法:哥哥割格個個革
①實數解分割(UserCut)
“如上圖,有這麼一個整數規劃問題,黑色線段是線性不等式,藍色的點是離散的可行域,藍色線段包圍的空間是IP Hull(整數解形成的凸包,NP-hard to find,因為一旦找到,那麼求解整數規劃隻需要求解凸包這個LP問題),在其外面黑色線段的包圍是LP Hull(線性松弛解形成的凸包)
正是因為IP Hull和LP Hull中間的間隙,使得該LP的最優解是fractional(對于原問題infeasible)的,而這段間隙,對于LP(線性規劃)來講,是多餘的搜尋空間。如果我們在這個時候可以加上一個或多個線性不等式(cut),把無用空間完全“砍”掉,那麼LP Hull = IP Hull,這時我們就得到整數解了
當然一般情況沒有這麼好運,可以把無用空間完全砍掉。如上圖,加上紅色虛線這個cut,我們砍掉了紅色陰影區域這部分無用空間。雖然沒有把LP Hull直接縮小成IP Hull這麼立竿見影,但對于求解原問題,由于減少了搜尋空間,也是一種效率上的提升
另外值得注意的是,紅色虛線的cut,對于原問題(IP Hull)也是滿足的(valid),它砍掉的,隻是實數部分無用的搜尋空間”
②整數解分割(LazyCut)
“如上圖,我們有IP hull和LP hull,我們加上一個Lazy Constraints,這時候把頂上三個原問題的可行整數解也砍掉了
割平面法最經典的應用,莫過于Travelling Salesman Problem,個問題是每個學運籌學特别是組合優化必學的經典問題”
“如上圖,TSP需要找從一點出發,周遊所有城市(1-6點)再回到出發點的cycle(回路)。為了簡化問題,在master problem(初始問題)的表達式中,我們忽略subtour(小的cycle,例如上圖4-5-6)限制(因為有指數級個數該限制),然後求解該IP問題
忽略掉subtour求得的IP問題雖然是整數可行解,但是其中可能存在subtour(如上圖倆個subtour),是以其實并不是我們想要的解。這時候,我們設計一個啟發式算法,來探測這些subtour,然後加上相應的cut砍掉這些subtour對應的整數解,然後再次求解IP。由此循環,直到求得的IP整數解中,不再存在subtour,這時候我們找到了最終問題的全局最優解”
PS:了解就行,其實這個系列的問題,
intlinprog
走天下,實在不行轉戰
linpog
,淺嘗辄止即可
割平面在計算機視覺有所應用,==attention==
咱們還是接着上面來
截取平面之後,怎樣求出$x_1 =1 \ , \ x_2 = 1\ , \ z = 2$?
這個時候就需要:
引入松弛變量: (解出x1=1,x2=1,z=2的過程)
引入之後的效果與原先是一緻的
如:$-x_1+x_2<=1$引入$x_3\geq 0$$之後得到$$-x_1+x_2+x_3=1$$則此時$$-x_1+x_2\leq 1$$任然成立,是以不影響結果
$$
max\ Z = x_1 + x_2\
\begin{cases}{}
-x_1 + x_2 + x_3\leq 1\
3x_1 + x_2 + x_4\leq 4\
x_1\ ,\ x_2 \ ,\ x_3\ ,\ x_4\geq 0\
x_1\ ,\ x_2 \ ,\ x_3\ , \ x_4\ are\ integers
\end{cases}
$$
上面兩個式子通過一定的轉化可以轉化為:
$$
x_1-\frac{1}{4}x_3+\frac{1}{4}x_4 = \frac{3}{4}\ \ (1)\
{}\
x_2 + \frac{3}{4}x_3 + \frac{1}{4}x_4 = \frac{7}{4}\ \ (2)
$$
然後再把整數部分(系數為整數與單個整數)放在左邊,小數部分放在右邊(系數為小數+單個小數)
$$
(1-0)x_1 + (-1 + \frac{3}{4})x_3 + (0 + \frac{1}{4})x_4 = 0+\frac{3}{4}
$$
整理為整數部分=小數部分!!!
$$
x_1 - x_3 = \frac{3}{4}-(\frac{3}{4}x_3 + \frac{1}{4}x_4)
$$
也就是:
$$
\frac{3}{4}-正數=一個整數\
{}\
而且0\leq \frac{3}{4}\leq 1 \ \ \ x_3\ ,\ x_4>=0\
{}\
是以 ,\ \ \frac{3}{4}-正數\leq0\
{}\
是以 \ \ 3x_3+x_4\geq3\ (1)\ and\ 4x_2+3x_3+x_4 \geq 7\ (2)
$$
基本流程:
引入松弛變量,變不等式為等式$a_{ik}x_k$松弛變量
$a_{ik}=[a_{ik}]+f_{ik}$松弛變量的系數化為正數部分和小數部分
$[a_{ik}]\ ,\ x_k$正數部分彙合
$f_{ik}\ ,\ x_k$小數部分彙合
$[a_{ik}]x_k -[b_i]$整數部分放在左側
$[b_i]+f_i$小數部分放在右側
function [intx,intf] = DividePlane(A,c,b,baseVector)
%功能:用割平面法求解整數規劃
%調用格式:[intx,intf]=DividePlane(A,c,b,baseVector)
%其中, A:限制矩陣;
% c:目标函數系數向量;
% b:限制右端向量;
% baseVector:初始基向量;
% intx:目标函數取最值時的自變量值;
% intf:目标函數的最值;
sz = size(A);
nVia = sz(2);%擷取有多少決策變量
n = sz(1);%擷取有多少限制條件
xx = 1:nVia;
if length(baseVector) ~= n
disp('基變量的個數要與限制矩陣的行數相等!');
mx = NaN;
mf = NaN;
return;
end
M = 0;
sigma = -[transpose(c) zeros(1,(nVia-length(c)))];
xb = b;
%首先用單純形法求出最優解
while 1
[maxs,ind] = max(sigma);
%--------------------用單純形法求最優解--------------------------------------
if maxs <= 0 %當檢驗數均小于0時,求得最優解。
vr = find(c~=0 ,1,'last');
for l=1:vr
ele = find(baseVector == l,1);
if(isempty(ele))
mx(l) = 0;
else
mx(l)=xb(ele);
end
end
if max(abs(round(mx) - mx))<1.0e-7 %判斷最優解是否為整數解,如果是整數解。
intx = mx;
intf = mx*c;
return;
else %如果最優解不是整數解時,建構切割方程
sz = size(A);
sr = sz(1);
sc = sz(2);
[max_x, index_x] = max(abs(round(mx) - mx));
[isB, num] = find(index_x == baseVector);
fi = xb(num) - floor(xb(num));
for i=1:(index_x-1)
Atmp(1,i) = A(num,i) - floor(A(num,i));
end
for i=(index_x+1):sc
Atmp(1,i) = A(num,i) - floor(A(num,i));
end
Atmp(1,index_x) = 0; %建構對偶單純形法的初始表格
A = [A zeros(sr,1);-Atmp(1,:) 1];
xb = [xb;-fi];
baseVector = [baseVector sc+1];
sigma = [sigma 0];
%-------------------對偶單純形法的疊代過程----------------------
while 1
%----------------------------------------------------------
if xb >= 0 %判斷如果右端向量均大于0,求得最優解
if max(abs(round(xb) - xb))<1.0e-7 %如果用對偶單純形法求得了整數解,則傳回最優整數解
vr = find(c~=0 ,1,'last');
for l=1:vr
ele = find(baseVector == l,1);
if(isempty(ele))
mx_1(l) = 0;
else
mx_1(l)=xb(ele);
end
end
intx = mx_1;
intf = mx_1*c;
return;
else %如果對偶單純形法求得的最優解不是整數解,繼續添加切割方程
sz = size(A);
sr = sz(1);
sc = sz(2);
[max_x, index_x] = max(abs(round(mx_1) - mx_1));
[isB, num] = find(index_x == baseVector);
fi = xb(num) - floor(xb(num));
for i=1:(index_x-1)
Atmp(1,i) = A(num,i) - floor(A(num,i));
end
for i=(index_x+1):sc
Atmp(1,i) = A(num,i) - floor(A(num,i));
end
Atmp(1,index_x) = 0; %下一次對偶單純形疊代的初始表格
A = [A zeros(sr,1);-Atmp(1,:) 1];
xb = [xb;-fi];
baseVector = [baseVector sc+1];
sigma = [sigma 0];
continue;
end
else %如果右端向量不全大于0,則進行對偶單純形法的換基變量過程
minb_1 = inf;
chagB_1 = inf;
sA = size(A);
[br,idb] = min(xb);
for j=1:sA(2)
if A(idb,j)<0
bm = sigma(j)/A(idb,j);
if bm<minb_1
minb_1 = bm;
chagB_1 = j;
end
end
end
sigma = sigma -A(idb,:)*minb_1;
xb(idb) = xb(idb)/A(idb,chagB_1);
A(idb,:) = A(idb,:)/A(idb,chagB_1);
for i =1:sA(1)
if i ~= idb
xb(i) = xb(i)-A(i,chagB_1)*xb(idb);
A(i,:) = A(i,:) - A(i,chagB_1)*A(idb,:);
end
end
baseVector(idb) = chagB_1;
end
%------------------------------------------------------------
end
%--------------------對偶單純形法的疊代過程---------------------
end
else %如果檢驗數有不小于0的,則進行單純形算法的疊代過程
minb = inf;
chagB = inf;
for j=1:n
if A(j,ind)>0
bz = xb(j)/A(j,ind);
if bz<minb
minb = bz;
chagB = j;
end
end
end
sigma = sigma -A(chagB,:)*maxs/A(chagB,ind);
xb(chagB) = xb(chagB)/A(chagB,ind);
A(chagB,:) = A(chagB,:)/A(chagB,ind);
for i =1:n
if i ~= chagB
xb(i) = xb(i)-A(i,ind)*xb(chagB);
A(i,:) = A(i,:) - A(i,ind)*A(chagB,:);
end
end
baseVector(chagB) = ind;
end
M = M + 1;
if (M == 1000000)
disp('找不到最優解!');
mx = NaN;
minf = NaN;
return;
end
end
f = [-20 , -14 , -16 , -36 , -32 , -30]; % 不要加松弛變量
A = [0.01 0.01 0.01 0.03 0.03 0.03 1 0 0 0;
0.02 0 0 0.05 0 0 0 1 0 0;
0 0.02 0 0 0.05 0 0 0 1 0;
0 0 0.03 0 0 0.08 0 0 0 1]; % 加上松弛變量
b = [850 700 100 900];
[intx , intf] = DividePlane(A,c,b,[7 8 9 10]); % 松弛變量 7 8 9 10
intx
intf = -intf
----------
Output
intx =
35000 5000 30000 0 0 0
intf =
1250000