A - Game of Sum
dp[i, j]表示區間[i, j]範圍内能選擇的最大數。這個最大數不管是A還是B，也就是說可以當作是A B交替的。
由于區間範圍是不斷擴張的，是以求大區間的最大值時就要向小區間詢問，此時小區間相當于是個Oracle，無所不知，隻管負責問就行了。
于是對于此題A B可以從兩端選取任意多值，是以當A求dp[i, j]時需要詢問的區間（而且還要從兩端分别）為[i, k],[k+1, j]（i <= k < j）
詢問的這些子區間可以當作是B所能達到的最大值，使這些B最優值達到最小，即是A的目的。
最後還要考慮一點就是：如果A把區間[i, j]全部取完，還要和上述得到的結果作個比較。
#include <iostream>
#include<cstring>
#include<string>
#include<algorithm>
#include<cstdio>
#include<map>
#include<vector>
using namespace std;
const int maxn=100+5;
const int inf=0x3f3f3f3f;
int dp[maxn][maxn];
int sum[maxn];
int n;
void solve()
{
for(int p=2;p<=n;p++)
for(int i=1,j=p;j<=n;j++,i++)
{
int ans=-inf;
for(int k=i;k<j;k++) //判斷取走數目不同i-j值
{
int res=min(dp[i][k],dp[k+1][j]);
res=sum[j]-sum[i-1]-res;//B的最小取值，對應A的最大值
if(ans<res)
ans=res;
}
if(ans<sum[j]-sum[i-1])//需要比較全部取走
ans=sum[j]-sum[i-1];
dp[i][j]=ans;
}
}
int main()
{
while(cin>>n&&n)
{
memset(sum,0,sizeof(sum));
for(int i=1;i<=n;i++)
{
int x;
cin>>x;
dp[i][i]=x;
sum[i]=sum[i-1]+x;
}
solve();
printf("%d\n",2*dp[1][n]-sum[n]);//A-B = (A-(sum-A) = 2*A-sum
}
return 0;
}
；；
B - Brackets sequence
dp+遞歸
紫書p278
設 dp[i][j]表示第i個位置到第j個位置變成合法形式需要添加的字元數。
注意題目中的合法形式，1-->（A），2-->[A] , 3-->AB 。三種。
這裡 1.如果形式1或者2.則有 dp[i][j] = min(dp[i][j] , dp[i+1][j-1]) .
2.如果是形式3.則有 dp[i][j] = min(dp[i][j] , dp[i][k] + dp[k+1][j]) ,其中k>=i ,k < j ;
同時得注意 在遞推時，如論如何都要 進入到情況2.因為即使滿足形式1和2，不一定是所需添加的字母最少的情況，
例如: ()([])
還有就是遞推的方向問題。
當i== j 時 ,dp[i][i] = 1 ;
注意i < j .放到矩陣裡就是右上角的矩陣。
再者就是 遞推式。遞推式要求要先求出同一行的前面的值，還用同一列下面的值。
是以地推方向可以為 i從 n --> 0 ；j從0-->n.
#include <iostream>
#include<cstring>
#include<string>
#include<algorithm>
#include<cstdio>
#include<map>
#include<vector>
using namespace std;
const int maxn=100+5;
string s;
int dp[maxn][maxn];
int n;
int mach(int i,int j)
{
if((s[i]=='('&&s[j]==')')||(s[i]=='['&&s[j]==']'))
return 1;
return 0;
}
void fd()
{
for(int i=0;i<n;i++)
{
dp[i][i]=1;
dp[i+1][i]=0;
}
for(int i=n-2;i>=0;i--)
for(int j=i+1;j<n;j++)
{
dp[i][j]=n;
if(mach(i,j))
dp[i][j]=min(dp[i][j],dp[i+1][j-1]);
for(int k=i;k<j;k++)
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]);
}
}
void print(int i,int j)
{
if(i==j)
{
if(s[i]=='('||s[i]==')')
printf("()");
else
printf("[]");
return;
}
int ans=dp[i][j];
if(mach(i,j)&&ans==dp[i+1][j-1])
{
cout<<s[i];
print(i+1,j-1);
cout<<s[j];
return ;
}
for(int k=i;k<j;k++)
if(ans==(dp[i][k]+dp[k+1][j]))
{
print(i,k);
print(k+1,j);
return;
}
}
int main()
{
int T;
cin>>T;
getchar();
while(T--)
{
getline(cin,s);
getline(cin,s);
// cout<<"..."<<s<<endl;
n=s.size();
memset(dp,0,sizeof(dp));
fd();
print(0,n-1);
cout<<endl;
if(T!=0)
cout<<endl;
}
return 0;
}
;;
C - Robotruck
;;
D - Headmaster's Headache
;;
E - Blocks
;;
dp[l][r][k]表示将[l,r]區間連同之後的長度為k的一起消除的最大得分。
兩種決策如圖所示：
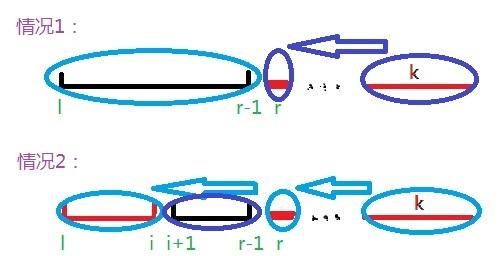
狀态轉移方程：dp[l][r][k] = max(dp[l][r-1][0] + (len[r]+k)^2, dp[l][i][len[r]+k] + dp[i+1][r-1][0]) (l <= i < r, color[i] = color[r])
用到了一個優化，現将相同顔色的分為一組，長度用len數組表示，之後的運算都在分組壓縮後重新編号的基礎上進行。
#include <iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=200+5;
int dp[maxn][maxn][maxn];
int cnt;
int color[maxn];
int len[maxn];
int s[maxn];
int DP(int l,int r,int k)
{
if(l>r)
return 0;
if(dp[l][r][k]!=-1)
return dp[l][r][k];
int res=DP(l,r-1,0)+(len[r]+k)*(len[r]+k);
for(int i=r-1;i>=l;i--)
if(color[i]==color[r])
res=max(res,DP(l,i,len[r]+k)+DP(i+1,r-1,0));
return dp[l][r][k]=res;
}
int main()
{
int T;
cin>>T;
for(int ka=1;ka<=T;ka++)
{
int n,x;
cin>>n;
cnt=0;
cin>>x;
int temp=x;
color[0]=temp;
len[cnt]=1;
for(int i=1;i<n;i++)
{
cin>>x;
if(x!=temp)
{
cnt++;
color[cnt]=x;
temp=x;
len[cnt]=1;
}
else
len[cnt]++;
}
// cout<<cnt<<endl;
memset(dp,-1,sizeof(dp));
printf("Case %d: %d\n",ka,DP(0,cnt,0));
}
return 0;
}
F - Party at Hali-Bula
樹形dp
我的一個小部落格：
點選打開連結
#include <iostream>
#include<cstring>
#include<string>
#include<algorithm>
#include<cstdio>
#include<map>
#include<vector>
using namespace std;
const int inf=0x3f3f3f3f;
const int maxn=200+5;
map<string,int>mp;
int n;
int vis[maxn];
vector<int> eg[maxn];
int flag;
int nn;
int ans;
int dp[maxn][3];
void dfs(int a,int ok)
{
if(eg[a].size()==0&&ok)
{
dp[a][1]=1;
dp[a][0]=0;
}
if(vis[a])
return;
if(ok)
{
dp[a][1]=1;
for(int i=0;i<eg[a].size();i++)
{ vis[a]=1;
dfs(eg[a][i],0);
dp[a][1]+=dp[eg[a][i]][0];
}
}
dp[a][0]=0;
for(int i=0;i<eg[a].size();i++)
{
dfs(eg[a][i],1);
dp[a][0]+=max(dp[eg[a][i]][1],dp[eg[a][i]][0]);
}
if(dp[a][0]==dp[a][1])
flag=1;
}
int oj(int a,int ok)
{
if(ok)
{
for(int i=0;i<eg[a].size();i++)
if(oj(eg[a][i],0))
return 1;
}
else
{
for(int i=0;i<eg[a].size();i++)
{
if(dp[eg[a][i]][0]==dp[eg[a][i]][1])
return 1;
}
}
return 0;
}
int main()
{
string a,b;
while(cin>>n&&n)
{
cin>>a;
int num=1;
mp.clear();
for(int i=0;i<=n;i++)
eg[i].clear();
mp[a]=num;
for(int i=0;i<n-1;i++)
{
cin>>a>>b;
if(!mp[a])
{
num++;
mp[a]=num;
}
if(!mp[b])
{
num++;
mp[b]=num;
}
eg[mp[b]].push_back(mp[a]);
}
nn=0;
ans=0;
flag=0;
memset(vis,0,sizeof(vis));
memset(dp,0,sizeof(dp));
dfs(1,1);
ans=max(dp[1][0],dp[1][1]);
if(dp[1][0]==dp[1][1])
flag=1;
else
{
if(dp[1][0]>dp[1][1])
flag=oj(1,0);
else
flag=oj(1,1);
}
cout<<ans<<" ";
if(flag)
cout<<"No"<<endl;
else
cout<<"Yes"<<endl;
}
return 0;
}
![程式員的算法趣題Q09: 落單的男女1. 問題描述2. 解題分析3. 代碼及測試4. 思考[圖]](data:image/gif;base64,R0lGODlhAQABAIAAAP///wAAACwAAAAAAQABAAACAkQBADs=)