【ELT.ZIP】OpenHarmony啃論文俱樂部——快速随機通路字元串壓縮

本文出自 ELT.ZIP 團隊，ELT<=>Elite(精英)，.ZIP為壓縮格式，ELT.ZIP即壓縮精英。
成員：
- 上海工程技術大學大二在校生
- 合肥師範學院大二在校生
- 清華大學大二在校生
- 成都資訊工程大學大一在校生
- 黑龍江大學大一在校生
- 華南理工大學大一在校生
我們是來自 7個地方 的同學，我們在 OpenHarmony成長計劃啃論文俱樂部 裡，與 華為、軟通動力、潤和軟體、拓維資訊、深開鴻 等公司一起，學習和研究 作業系統技術 ...

【往期回顧】

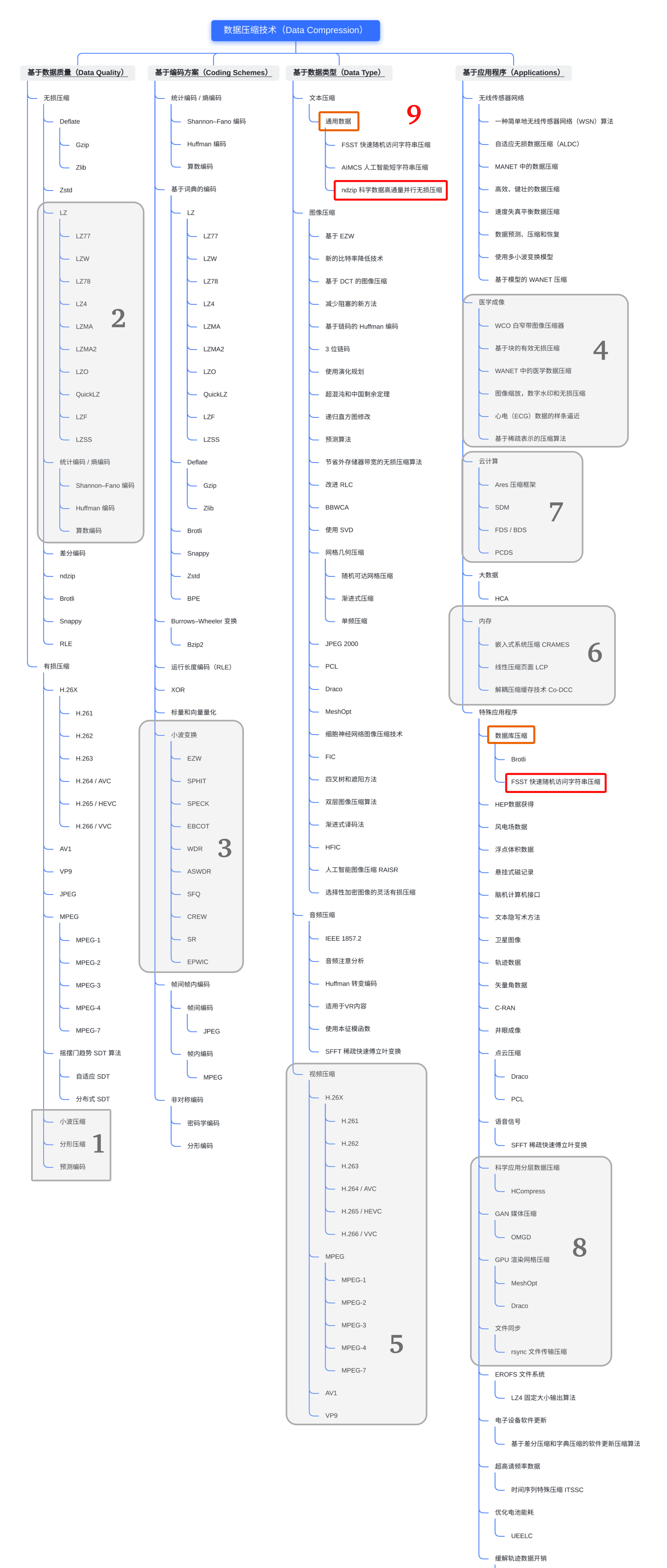
① 2月23日《老子到此一遊系列》之老子為什麼是老子 —— ++綜述視角解讀壓縮編碼++

② 3月11日《老子到此一遊系列》之老子帶你看懂這些風景 —— ++多元探秘通用無損壓縮++

③ 3月25日《老子到此一遊系列》之老子見證的滄海桑田 —— ++輕翻那些永垂不朽的詩篇++

④ 4月4日《老子到此一遊系列》之老子遊玩了一條河 —— ++細數生活中的壓縮點滴++

⑤ 4月18日 ++【ELT.ZIP】OpenHarmony啃論文俱樂部——一文穿透多媒體過往前沿++

⑥ 4月18日 ++【ELT.ZIP】OpenHarmony啃論文俱樂部——這些小風景你不應該錯過++

⑦ 4月18日 ++【ELT.ZIP】OpenHarmony啃論文俱樂部——淺析稀疏表示醫學圖像++

⑧ 4月29日 ++【ELT.ZIP】OpenHarmony啃論文俱樂部——計算機視覺資料壓縮應用++

⑨ 4月29日 ++【ELT.ZIP】OpenHarmony啃論文俱樂部——點燃主緩存壓縮技術火花++

⑩ 4月29日 ++【ELT.ZIP】OpenHarmony啃論文俱樂部——即刻征服3D網格壓縮編碼++

⑪ 5月10日 ++【ELT.ZIP】OpenHarmony啃論文俱樂部——雲計算資料壓縮方案++

⑫ 5月10日 ++【ELT.ZIP】OpenHarmony啃論文俱樂部——大資料架構性能優化系統++

⑬ 5月10日 ++【ELT.ZIP】OpenHarmony啃論文俱樂部——物聯網搖擺門趨勢算法++

⑭ 5月22日 ++【ELT.ZIP】OpenHarmony啃論文俱樂部——電子裝置軟體更新壓縮++

⑮ 5月22日 ++【ELT.ZIP】OpenHarmony啃論文俱樂部——人工智能短字元串壓縮++

⑯ 5月22日 ++【ELT.ZIP】OpenHarmony啃論文俱樂部——多層存儲分級資料壓縮++](https://ost.51cto.com/posts/13061)

【本期看點】

FSST思想核心
FSST的演化
FSST與LZ4對比
親手複現FSST

【技術DNA】

【智慧場景】

**********	********************	********************	********************	********************	********************	********************	********************	********************	********************	********************	********************	********************	********************	********************	*****************
場景	自動駕駛 / AR	語音信号	流視訊	GPU 渲染	科學、雲計算	記憶體縮減	科學應用	醫學圖像	資料庫伺服器	人工智能圖像	文本傳輸	GAN媒體壓縮	圖像壓縮	檔案同步	資料庫系統
技術	點雲壓縮	‎稀疏快速傅裡葉變換‎	有損視訊壓縮	網格壓縮	動态選擇壓縮算法架構	無損壓縮	分層資料壓縮	醫學圖像壓縮	無損通用壓縮	人工智能圖像壓縮	短字元串壓縮	GAN 壓縮的線上多粒度蒸餾	圖像壓縮	檔案傳輸壓縮	快速随機通路字元串壓縮
開源項目	Draco / 基于深度學習算法/PCL/OctNet	SFFT	AV1 / H.266編碼 / H.266解碼/VP9	MeshOpt / Draco	Ares	LZ4	HCompress	DICOM	Brotli	RAISR	AIMCS	OMGD	OpenJPEG	rsync	FSST

FSST

快速靜态符号表(FSST)壓縮，這是一種輕量級的字元串編碼方案。

引言：

::: hljs-left

• 字元串在現實世界的資料集中很普遍。它們通常占用大量資料，處理速度很慢。

• 在許多真實的資料庫中，很大一部分資料是用字元串表示的。

• 這是因為字元串經常被用作各種資料的萬能類型。

• 人工生成的文本(描述或評論字段)

:::

• 機器生成的辨別符(url、電子郵件位址、IP 位址）

1. 字元串處理的現有方案

• 字元串通常是高度可壓縮的，許多系統依賴字典來壓縮字元串。但是字典壓縮需要完全重複字元串來減少大小，是以當字元串相似但不相等時，字典壓縮沒有優勢。存儲在資料庫中的大多數字元串每個字元串通常小于 30 位元組。LZ4 就不适合壓縮小的、單個的字元串，因為它們需要達到 KB 數量級的輸入大小才能獲得良好的壓縮因子。但是，資料庫系統通常所需是對單個字元串随機通路，而LZ4算法是通過對資料塊的通路實作的，這就無法滿足資料庫系統的需求。

2.主要特點

• 随機通路(解壓縮單個字元串而無需解壓縮一個更大的塊的能力)

• 快速解碼(≈1-3 周期/位元組，或 1-3 GB/s 每個核)

• 文本字元串資料集的良好壓縮因子(≈2×)

• 高編碼性能(≈4 個周期每位元組，或≈1 GB每秒每位元組)

3.關鍵思想

• 是用 1 位元組代碼替換頻繁出現的最多 8 位元組的子字元串，這些元素構成一個不可變符号表。

4.前人的積澱

•

資料庫系統輕量級壓縮

的研究集中在

整數資料

，但字元串在現實工作負載中的普遍存在和性能挑戰需要進行更多的研究。壓縮字元串最常用的方法是使用

字典重複資料删除

。字典将每個唯一的字元串映射為整數代碼，使用整數壓縮方案對這些代碼進行壓縮。在大多數資料庫系統中，字元串本身沒有被壓縮。

Binnig 等人提出了一個帶 增量字首壓縮 的 保序字元串
字典。

字典被表示為一個混合的 try /B-tree 資料結構，以排序的順序存儲唯一的字元串。雖然對某些資料集(例如 url)有效，但許多其他常見字元串資料集(例如 uuid)沒有長時間的
共享字首 ，這使得該方案無效。全局字典還有如 更新昂貴
等缺點，這阻礙了它們的廣泛采用。
另一種壓縮字元串字典的方法是由 Arz 和 Fischer提出

他們開發了
LZ78的變體 ，允許 解壓單個字元串 。但是，這種方法的解壓縮 非常昂貴
，對于平均長度為 19 的字元串，需要超過 1 微秒的時間。這相當于每個字元大約 100 個 CPU 周期或每秒幾十兆位元組，這對于許多資料管理用例來說太慢了。
PostgreSQL

不使用字元串字典，而是實作了一種叫做
“超大屬性存儲技術”(TOAST)
的方法。大于 2 KB 的進行壓縮，較小的值保持不壓縮。
位元組對

此方案是少數
允許解壓縮單個短字元串 的壓縮方案之一。它首先對資料執行一次完整的傳遞，确定哪些位元組值沒有出現在輸入中，并計算每對位元組出現的頻率。然後用未使用的位元組值替換最常見的位元組對。重複這個過程，直到沒有更多未使用的位元組。位元組對對未使用位元組的依賴意味，給定一個現有的壓縮表，不可見的資料不能被壓縮。位元組對的遞歸性質使 解壓縮疊代，速度很慢
。
遞歸配對

一種
随機通路壓縮格式 ，它遞歸地構造 層次符号文法
。初始文法由所有單位元組符号組成，通過将源文本中頻率最高的連續符号對替換為一個新符号、相對于擴充的文法重新計算所有符号對的頻率，并遞歸地進行擴充。

主要步驟
制靜态符号表

識别經常出現的
公共子字元串 (稱之為符号)，并将它們替換為短的、固定大小的代碼，由于效率的原因，符号的長度在 1 到 8 位元組之間，并在位元組(而不是位)邊界上進行辨別。代碼總是 1 位元組長，這意味着最多可以有 256 個符号，其中一個碼被保留為 轉義碼 .
解壓縮

解壓縮是相當簡單的。每段代碼都通過
數組查找 轉換為其符号，并将符号追加到輸出緩沖區。為了有效地解壓縮，将每個符号表示為一個 8 位元組(64 位)的單詞，并将所有符号存儲在一個數組中。此外，還有第二個數組，用于存儲每個單詞的長度。使用這種表示，可以無條件地将 64 位字存儲到輸出緩沖區中，然後将輸出緩沖區向前推進符号的實際長度來解壓代碼，依賴于現代處理器上可用的 快速未對齊存儲 ，這種實作需要 很少的指令 ，而且 沒有分支 。它的 緩存效率也很高
，因為符号表(2048 位元組)和長度數組(256 位元組)都可以輕松地放入一級 CPU 緩存中。
幾點解釋

::: hljs-left

1.使用轉義字元的優勢

PS：（轉義碼并不是嚴格必要的;也可以隻使用那些沒有出現在輸入字元串中的位元組作為代碼）

直接原因：保留代碼 255 作為轉義标記，表示輸入中的以下位元組需要按原樣複制，而不需要在符号表中查找。

三個優點

（1）支援使用現有的符号表

壓縮任意

(看不見的)文本。

（2）允許在

資料樣本

上執行符号表

構造

，進而加速壓縮。

（3）它

釋放

了原本被保留為

低頻位元組的符号

，進而

提高了壓縮因子

。

2.連續注入單位元組符号

如果由兩個

較短

的符号

合并建立

一個

較長

的符号，如果較長的符号再之後的

增益排序

中處于

末尾

就會被其他增益較長的字元串

取代

，這也就意味着

原先

那兩個

較短

的字元串也就

随之消失

。

從本質上說，如果不考慮單位元組，符号隻會變長，如果這樣更好的話，就永遠不可能回到更短的符号。連續注入單位元組符号允許

重新生長

由于這種

太貪婪

的選擇而丢失的有價值的長符号。

FSST良好屬性

保有字元串屬性：不會因為編碼轉化變成其他類型的文本。
壓縮查詢處理。直接通過比較其再表中的符号即可。
字元串比對。也可以對壓縮的字元串執行更複雜的經常發生的字元串操作(例如，LIKE 模式比對)，通過轉換為位元組流中識别它們而設計的自動機，将它們重新映射到代碼流中。
符号表很小。符号表的最大大小為 8*255+255 位元組，但通常隻占用幾百位元組，因為平均符号長度通常在 2 左右。是以，使用單獨的符号表壓縮每個字元串列的每個頁面是完全可行的，但也可以采用更粗粒度的粒度(按行組或整個表)。更細粒度的符号表構造會帶來更好的壓縮因子，是以符号表将更适合于壓縮的資料。
并行性。由于沒有(解)壓縮狀态，FSST(解)壓縮并行化很簡單——隻有符号表構造算法可能需要序列化。另一方面，讓每個批量加載資料塊的線程構造一個單獨的符号表 (應該放在每個塊頭中)也是可以接受的，這樣壓縮也會變得非常并行。
0-terminated 字元串。FSST 可選地生成以 0 結尾的字元串，因為在以 0 結尾的字元串中位元組隻出現在每個字元串的末尾，實際上還有 254 個代碼需要壓縮。這稍微降低了壓縮的級别(價值最低的 255 個符号必須從符号表中删除，它的出現将使用轉義位元組進行處理)，但這種可選模式允許 FSST 适應許多現有的基礎結構。

:::

5.存在問題

重複

首先計算長度為 1 到 8 的子字元串在資料中出現的頻率，然後根據
增益順序 選擇前 255 個符号。這種方法的問題是: 選擇的符号可能重疊 ，是以計算的增益會被 高估 。例如，在 URL 資料集中，8 位元組符号 http://w 幾乎每個字元串都含有，最有希望被選中。但符号 ttp://ww 和 tp://www 看起來同樣有希望，将所有三個候選者添加到符号表中是對有限代碼數量的浪費，并會對壓縮因子産生負面影響。
貪婪性

在編碼期間貪婪地
選擇最長 的符号不一定能最大化壓縮效率。參考我們在上文提到的 連續單位元組注入 .
綜上所述，符号重疊與貪婪編碼相結合，造成符号之間的依賴問題，這使得難以估計增益，進而建立良好的符号表。

優化方案

::: hljs-left

（1)疊代語料庫，使用目前的符号表

動态編碼

。這個階段

計算

符号表的整體品質

(壓縮因子)

，但也計算每個符号在壓縮表示中的

出現頻率

，以及每個

連續符号對

。

(2)利用這些計數，通過選擇

表觀增益最高

的符号來

建構一個新的符号表

。

執行個體

語料庫“tumcwitumvldb”上的 4 次疊代。為了使示例易于說明，将最大符号長度限制為 3(而不是 8)，最大符号表大小限制為 5(而不是 255)。在每次疊代之後，在頂部顯示壓縮後的字元串，但為了可讀性，不顯示代碼，而是顯示相應的符号。“$”表示轉義位元組。

:::

這是最初未壓縮的字元串

在第一次疊代中，壓縮字元串的長度 臨時加倍 ，因為符号表 最初是空的 ，每個符号都必須轉義。在圖的底部，我們顯示了符号表，前 5 位符号基于 靜态增益 。

【ELT.ZIP】OpenHarmony啃論文俱樂部——快速随機通路字元串壓縮

疊代 1 後，靜态增益排名前 5 位的為“um”、“tu”、“wi”，“cw” 和 “mc”。前兩個最上面的符号(“um”，“tu”)出現了兩次，是以增益為 4，而後三個符号(“wi”，“cw”和“mc”)隻出現一次，是以增益為 2。注意，符号“mv”，“vl”，“ld”，“db”， “m”，“t”，“u”的增益也為 2，也可以被選取。換句話說，當選擇頂部符号時，算法會

任意地選取

。

在第 2、3 和 4 次疊代中，符号表的 品質穩步提高 。

疊代 4 之後，最初長度為 13 的語料庫被壓縮為 5。

【ELT.ZIP】OpenHarmony啃論文俱樂部——快速随機通路字元串壓縮
圖中還顯示，算法也 會出現錯誤 ，但這些錯誤會在 下一次疊代中得到修複 。
例如，在第 2 次疊代中，符号“tu”看起來相當有吸引力，靜态增益為 4，但由于“tum”也在符号表中，“tu”最終變得毫無價值

并在第 3 次疊代中被修正

【ELT.ZIP】OpenHarmony啃論文俱樂部——快速随機通路字元串壓縮

技術優化：

AVX512壓縮

第一步，FSST API 壓縮一批字元串，字元串被複制到一個由 512 個段組成的臨時

緩沖區

中，如果需要将

分割

長字元串，并添加

終止符

。

第二步，首先按反向字元串長度對作業隊列數組進行

基數排序

——速度很快，隻需一次傳遞——是以首先處理最長的字元串，這有助于

負載平衡

。作業可能以不連續的順序完成，是以由于排序而以不連續的作業順序開始編碼工作，不會使算法(進一步)複雜化。

第三步，AVX512 的優勢不是記憶體通路，而是在壓縮核心中利用的

并行計算

。不隻是一次性啟動

SIMD 核心

來處理 8 個通道中的 8 個字元串(或 24 個通道中的 24 個字元串，3×展開)，因為有些字元串會比其他字元串短得多，而有些字元串會比其他字元串壓縮得多。這将意味着在編碼工作結束時，許多通道将是空的。是以，緩沖 512 個作業，并在需要時在每次疊代中重新填充車道。退出作業(作業控制寄存器中的通道 )使用

compress_store 指 令

，并填充

expand_load 指令

。

FSST 與LZ4對比

· 速度

上表顯示了 LZ4 和 FSST 在每個資料集上分别和平均的三個名額的相對性能。

對于幾乎所有的資料集，FSST 在壓縮因子和壓縮速度方面都優于 LZ4。平均而言，除了産生更好的壓縮因子 FSST 的壓縮速度也提高了 60%。對于解壓速度，FSST 在某些資料集上更快，而 LZ4 在其他資料集上更快——平均速度幾乎相同。

· 随機存取

在資料庫場景中，通常不存儲大檔案，而是使用包含大量相對較短字元串的字元串屬性或字典。用 LZ4 單獨壓縮這些字元串會得到非常差的壓縮系數，普通 LZ4 (LZ4 行)不能合理地處理短字元串—壓縮因子低于 1，這意味着資料大小實際上略有增加。LZ4 還可選地支援使用額外的字典，該字典需要與壓縮資料一起提供。使用 zstd 預生成一個适合語料庫的字典(LZ4 字典)，在一定程度上提高了壓縮因子，但嚴重影響了壓縮速度。

下圖是測試結果

· 分文本資料

資料庫環境之外，壓縮社群經常評估

Silesia 語料庫

上的壓縮方法，該語料庫由 11 個檔案組成，其中 4 個是

文本檔案(dick- ens, reymont, mr, webster)

，1個是

XML

, 6 個是

二進制檔案

。FSST 對文本檔案的壓縮大小平均提高了 10%，但對二進制檔案的壓縮大小平均降低了 25%。雖然認為二進制檔案與 FSST 無關，但它在大型

XML

和

JSON 檔案

上的

壓縮比

比 LZ4 差 2-2.5 倍，這是相關的。但是，資料庫系統不應該将這些組合值存儲為簡單的字元串，而應該存儲為允許查詢處理的特殊類型。例如，

Snowflake

識别 JSON 列中的結構，并在内部将

每個經常出現的 JSON 屬性存儲在單獨的内部列中。

FSST的演化

FSST 壓縮算法經過多次疊代才達到目前的設計。上表顯示了 7 種變體的

壓縮因子(CF)、符号表建構成本(CS)和字 符串編碼速度(SE)

第一個設計基于字尾數組，壓縮因子達到1.97，但符号表的構造需要 74.3 cy- cles/位元組，編碼需要 160 cycles/位元組。

目前的 AVX512 版本(圖中的變體 7)在表建構方面快了 90 倍，快了40倍用于編碼比第一個版本-同時提供更高的壓縮因子。

最終的版本也比最初的 FSST 版本(變體 4)快得多，這要歸功于損耗完美哈希和 AVX512——盡管不得不犧牲相對于變體 4 大約 6%的空間增益。

盡管需要多次疊代，但符号表的構造時間隻占編碼時間的一小部分。優化構造需要将疊代次數從 10 次減少到 5 次，建構一個示例(每次疊代都會增長)，并縮小計數器的記憶體占用。

複現流程

系統需求

Linux、Windows、MacOS 均可，此處以 Linux 環境進行示範。

源碼準備

首先，來到 FSST 的開源倉庫 https://github.com/cwida/fsst，在已配置 Git 環境的情況下可以按照如圖所指位置複制 https 或 ssh 位址将源碼克隆至本地；若未配置 Git，可參考 github 或 gitee 的相關訓示進行配置操作。不過，Git 在此處并非必要條件，也可手動 "Download ZIP" 得到壓縮包後進行解壓。

【ELT.ZIP】OpenHarmony啃論文俱樂部——快速随機通路字元串壓縮
如上所述，針對 Git 環境，在終端中鍵入以下指令：

git clone https://github.com/cwida/fsst.git    # 若已配置SSH公鑰，可采用下圖形式
cd fsst/

環境搭建

1. CMake 安裝

FSST 使用 C++ 語言實作，依賴 CMake 工具進行編譯建構，Debian 系下可友善地使用 apt 實作安裝初始化，鍵入并執行以下指令：

sudo apt update
sudo apt install cmake

可以看到 cmake 在之前已經安裝過了，并且版本是 3.18.4 ：

2. Zstd 與 LZ4 庫的安裝

FSST 需要調用 zstd 與 lz4 的相關 API 以在壓縮過程中生成對應字典，是以還需要準備相應的動态庫：

sudo apt install zstd* lz4* libzstd* liblz4*   # 同 cmake 的安裝

完成後，可以在 /usr/lib/x86_64-linux-gnu/ 下看到相關檔案已生成：

此外，還需要建立到 /usr/lib/ 的軟連結，避免後續連結時出現找不到預設目錄的問題：

# 注意，下方諸如 '1.4.8' '1.8.3' 一類的版本号需要根據實際狀況進行相應地替換
cd /usr***/lib/x86_64-linux-gnu/
echo '../libzstd.so ../libzstd.so.1 ../libzstd.so.1.4.8' | sudo xargs -n 1 ln -s libzstd.so.1.4.8
echo '../liblz4.so ../liblz4.so.1 ../liblz4.so.1.8.3' | sudo xargs -n 1 ln -s liblz4.so.1.8.3

編譯建構

環境部署基本完成，下面開始編譯。

cd -
cmake ./
make -j8 && make binary

100% 完成後，說明編譯已成功，檢視所在目錄，可以看到 fsst 的二進制程式已生成：

為了友善後續操作，建議将其加入環境變量：

vim ~/.bashrc
export PATH=/home/yanxu/ELT.ZIP/fsst:$PATH    # 在尾行添加
:wq    # 儲存退出

已經可以正常使用，輸入 fsst 即可檢視說明：

評估測試

1. 自動化測試

倉庫中提供了足量的資料集用來對算法進行評估，并且也有自動化腳本幫助一鍵跑完全程，下面就來試一試吧：

cd paper/
chmod +x *.sh

results 目錄中已存放有作者測試過的結果，但我們同樣可以在自己機器上再跑一遍測試，執行如下指令：

make experiments

花費時間會較長，耐心等待即可，這裡舉出作者的其中一項示例：

最左側的一列是各式各樣的字元集，另外三個框框分别表示壓縮比、壓縮速度、解壓速度，其中，左側是 LZ4、右側是 FSST。不難看出，壓縮比方面，FSST 僅在 urls 上較 LZ4 弱了一點；壓縮速度方面，LZ4 僅在 hex 上取得了微弱的優勢；而解壓速度方面，則是二者互有勝負，可視作忽略不計。

看看 urls 和 hex 的差異究竟是怎樣：

【ELT.ZIP】OpenHarmony啃論文俱樂部——快速随機通路字元串壓縮

hex 是十六進制字元，urls 是文本連結，它們都是機器可讀的辨別符。

2. 手動測試

那麼除此之外，我們還可以手動進行對更多算法的對比。

參考文獻：

[1] Boncz P, Neumann T, Leis V. FSST: fast random access string compression[J]. Proceedings of the VLDB Endowment, 2020, 13(12): 2649-2661.

附件連結：https://ost.51cto.com/resource/2021