概述
在這篇部落格中我主要講解最短路徑算法中的Floyd算法,這是針對多源最短路徑的一個經典算法。對于單源最短路徑算法請詳見我的另一篇部落格:最短路徑算法(上)——迪傑斯特拉(Dijikstra)算法
弗洛伊德(Floyd)算法是解決任意兩點間的最短路徑的一種算法,可以正确處理有向圖或有向圖或負權(但不可存在負權回路)的最短路徑問題,同時也被用于計算有向圖的傳遞閉包。
算法思想與過程
(一)算法思想:
Floyd算法是一個經典的動态規劃算法。用通俗的語言來描述的話,首先我們的目标是尋找從點i到點j的最短路徑。從動态規劃的角度看問題,我們需要為這個目标重新做一個诠釋(這個诠釋正是動态規劃最富創造力的精華所在)。
從任意節點i到任意節點j的最短路徑不外乎2種可能,一是直接從i到j,二是從i經過若幹個節點k到j。是以,我們假設Dis(i,j)為節點u到節點v的最短路徑的距離,對于每一個節點k,我們檢查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,如果成立,證明從i到k再到j的路徑比i直接到j的路徑短,我們便設定Dis(i,j) = Dis(i,k) + Dis(k,j),這樣一來,當我們周遊完所有節點k,Dis(i,j)中記錄的便是i到j的最短路徑的距離。
(二)算法過程
1)首先把初始化距離dist數組為圖的鄰接矩陣,路徑數組path初始化為-1。其中對于鄰接矩陣中的數首先初始化為正無窮,如果兩個頂點存在邊則初始化為權重
2)對于每一對頂點 u 和 v,看看是否存在一個頂點 w 使得從 u 到 w 再到 v 比己知的路徑更短。如果是就更新它。
狀态轉移方程為
如果 dist[i][k]+dist[k][j] < dist[i][j]
則dist[i][j] = dist[i][k]+dist[k][j]
//Floyd算法(多源最短路徑算法)
bool Floyd(){
for(int k = 1 ; k < this->Nv+1 ; k++){ //k代表中間頂點
for(int i = 1 ; i < this->Nv+1 ; i++){//i代表起始頂點
for(int j = 1 ; j < this->Nv+1 ; j++){//j代表終點
if(this->dist[i][k] + this->dist[k][j] < this->dist[i][j]){
this->dist[i][j] = this->dist[i][k] + this->dist[k][j];
if(i == j && this->dist[i][j] < 0){//發現了負值圈
return false;
}
this->path[i][j] = k;
}
}
}
}
return true;
} 複制
例子
我們用如下圖結構來示範Floyd算法:
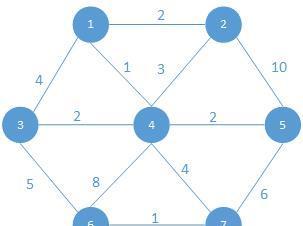
全部代碼為:
#include <iostream>
#include <cstring>
#include <stack>
#include <queue>
using namespace std;
const int MAX = 65535;
class Graph{
private:
int** G; // 鄰接矩陣
int** dist; // 距離數組
int** path; // 路徑數組
int Nv; // 頂點數
public:
//構造函數
Graph(int nv, int ne){
this->Nv = nv;
G = new int*[nv+1];
dist = new int*[nv+1];
path = new int*[nv+1];
for(int i = 0 ; i < nv+1 ; i++){
G[i] = new int[nv+1];
dist[i] = new int[nv+1];
path[i] = new int[nv+1];
memset(path[i],-1,sizeof(path[0][0])*(nv+1));
for(int j = 0 ; j < nv+1 ; j++){
this->G[i][j] = this->dist[i][j] = MAX;
}
this->G[i][i] = this->dist[i][i] = 0;
}
cout<<"請輸入邊與權重:"<<endl;
for(int i = 0 ; i < ne ; i++){
int v1,v2,weight;
cin>>v1>>v2>>weight;
this->G[v1][v2] = this->G[v2][v1] = weight;
this->dist[v1][v2] = this->dist[v2][v1] = weight;
}
}
//Floyd算法(多源最短路徑算法)
bool Floyd(){
for(int k = 1 ; k < this->Nv+1 ; k++){ //k代表中間頂點
for(int i = 1 ; i < this->Nv+1 ; i++){//i代表起始頂點
for(int j = 1 ; j < this->Nv+1 ; j++){//j代表終點
if(this->dist[i][k] + this->dist[k][j] < this->dist[i][j]){
this->dist[i][j] = this->dist[i][k] + this->dist[k][j];
if(i == j && this->dist[i][j] < 0){//發現了負值圈
return false;
}
this->path[i][j] = k;
}
}
}
}
return true;
}
// 分治法尋找start到end最短路徑的中間結點
void Find(queue<int> &q ,int start,int end){
int mid = this->path[start][end];
if(mid == -1){
return;
}
Find(q,start,mid);
q.push(mid);
Find(q,mid,end);
}
//列印start頂點到end頂點的路徑
void Print_Path(int start,int end){
queue<int> queue;
queue.push(start);
this->Find(queue,start,end);
queue.push(end);
cout<<queue.front();
queue.pop();
while(!queue.empty()){
cout<<"->"<<queue.front();
queue.pop();
}
cout<<endl;
}
void Print_Floyd(){
int i,j,k;
for(int i = 1 ; i < this->Nv+1 ; i++){
for(int j = 1 ; j < this->Nv+1 ; j++){
cout<<this->path[i][j]<<" ";
}
cout<<endl;
}
cout<<" length path"<<endl;
for(i = 1 ; i < this->Nv+1 ; i++){
for(j = i+1 ; j < this->Nv+1 ; j++){
cout<<i<<"->"<<j<<" ";
cout<<this->dist[i][j]<<" ";
this->Print_Path(i,j);
}
cout<<endl;
}
}
};
int main()
{
cout<<"請輸入頂點數與邊長數:"<<endl;
int nv,ne;
cin>>nv>>ne;
Graph graph(nv,ne);
if(graph.Floyd()){
cout<<"各個頂點的最短路徑為:"<<endl;
graph.Print_Floyd();
}
return 0;
} 複制
截圖如下: