1. 有一顆樹的括号表示為A(B, C(E, F(G)), D),回答下面的問題:
- 指出樹的根結點?
- 指出棵樹的所有葉子結點?
- 結點C的度是多少?
- 這棵樹的度為多少?
- 這棵樹的高度是多少?
- 結點C的孩子結點是哪?
- 結點C的雙親結點是誰?
答案:
這棵樹的根結點為A
這棵樹的葉子結點為B丶E丶G丶D // 葉子結點:一棵樹當中沒有子結點(即度為0)的結點稱為葉子結點,簡稱“葉子”。葉子是指出度為0的結點,又稱為終端結點。
結點C的度為2 // 結點度:結點擁有子結點的數量
這棵樹的度是3 // 二叉樹的度:是指樹中各結點度的最大值
這棵樹的高度為4 // 深度是從根節點到它的葉節點,高度是從葉節點數到它的根節點
節點C的孩子結點是E丶F
結點C的雙親結點是A 複制
2. 若一棵度為4的樹中度為2丶3丶4的結點個數分别為3丶2丶2,則該樹的葉子結點的個數是多少?
答案:
在樹中,結點有幾個分叉,度就是幾。
樹中結點數 = 總分叉樹 + 1。(這裡的分叉樹就是所有結點的度之和) 複制
❝ 那麼設葉子數為X,則此樹的總分叉樹為 2 * 3 + 3 * 2 + 4 * 2 = 20;樹中結點數 = 總分叉樹 + 1 = 20 + 1 = 21; 3 + 2 + 2 + X = 21,解得X = 14,即該樹的葉子結點的個數為14。
❞
3. 為了實作以下各種功能,其中X結點表示該結點的位置,給出樹的最适合的存儲結構:
- 求X和Y結點的最近祖先結點
- 求X結點的所有子孫
- 求根結點到X結點的路徑
- 求X結點的所有右邊結點的路徑
- 判斷X結點是否是葉子結點
- 求X結點的所有孩子
答案:
雙親存儲結構
孩子鍊存儲結構
孩子兄弟存儲結構
孩子存儲結構
孩子鍊存儲結構
孩子鍊存儲結構 複制
4. 設二叉樹BT的一種存儲結構如表7.1所示。其中,BT為樹根結點指針,Lichild丶rchild分别為結點的左丶右孩子指針域,在這裡使用結點編号作為指針域值,0表示指針域值為空;data為結點的資料域。請完成下列問題:
- 畫出二叉樹BT的樹形表示
- 寫出按先序丶中序和後續周遊二叉樹BT所得到的結點序列
- 畫出二叉樹BT的後續線索樹(不帶頭結點)
答案:
- BT的邏輯結構
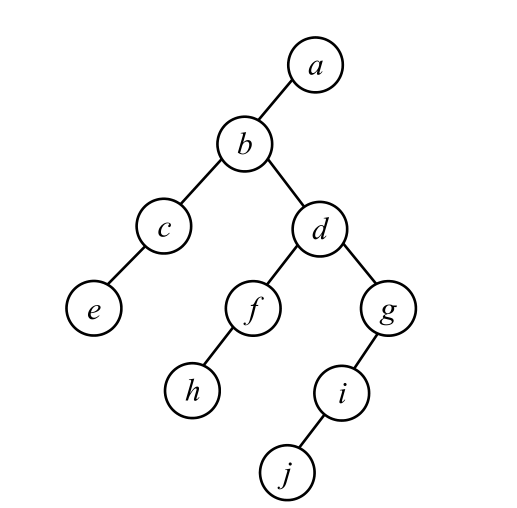
- 先序序列(根左右): abcedfhgij 中序序列(左根右): acbhfdjiga 後序序列(左右根): echfjigdba
- 先畫出周遊序列,後根據周遊序列例如ABC,看A的右子樹是否為空,如果為空,則指向B,再看B,如果B的左子樹為空,則指向A,以此類推,均符合這個規律。
5. 含有60個葉子結點的二叉樹的最小高度是多少?
答案
❝ 葉子結點:一棵樹中當中沒有子結點(即度為0)的結點,稱為葉子結點。葉子結點是指度為0的結點,又稱為終端結點。
❞
❝ 深度為h的二叉樹最多有2^h - 1個節點
❞
❝ n0: 指度(分叉)為0的結點 n1:指度(分叉)為1的結點 n2:指度(分叉)為2的結點
❞
❝ 二叉樹中的葉子節點個數等于度為2的節點個數+1: n0 = n2 + 1 證明連結
❞
答案:
在該二叉樹中,n0 = 60,
n = n0 + n1 + n2 = n0 + n1 + (n0 -1) = 60 + n1 + (60 - 1) = 119 + n1;
當n1= 0且為完全二叉樹時高度最小,
此時高度h = [log2^(n + 1)] = log(2)^120 = 7。是以含有60個葉子結點的二叉樹最小高度是7 複制
6. 已知一棵完全二叉樹的第6層(設根結點為第1層)有8個葉子結點,則該完全二叉樹的結點個數最多是多少?最少是多少?
❝ 滿二叉樹和完全二叉樹的差別:滿二叉樹:每層都達到最大數,稱為滿二叉樹。完全二叉樹:設二叉樹的高度為h層,其他各層(1~h-1)的結點數都達到最大個數,第h層從右向左連續缺若幹個結點。
❞
❝ 滿二叉樹也是完全二叉樹。
❞
答案:
完全二叉樹的葉子結點隻能在最下面兩層,是以結點最多的情況是第6層為倒數第2層,即1~6層構成一棵滿二叉樹,其結點總數為2^6-1=63。
其中第6層有2^5=32個結點,含8個葉子結點,則另外有32-8=24個非葉子結點,它們中每個結點有兩個孩子結點(均為第7層的葉子結點),計為48個葉子結點。
這樣最多的結點個數 = 63 + 48 = 111。
結點最少的情況是第6層為最小層,即1~5層構成一棵滿二叉樹,其結點總數為2^5 - 1 = 31,再加上第6層的結點,總計31 + 8 = 39。
這樣最少的結點個數為39。 複制
7. 已知一棵滿二叉樹的結點個數為20~40之間,此二叉樹的葉子結點有多少個?
答案:
滿二叉樹:除最後一層無任何子節點外,每一層上的所有結點都有兩個子結點的二叉樹。
一棵高度為h的滿二叉樹的結點個數為2(h) -1,有20<=2(h)-1<=40。
則h=5,滿二叉樹中葉子結點均集中在最底層,
是以葉子結點個數=2*(5-1) = 16個 複制
8. 已知一棵二叉樹的中序序列為cbedahgijf,後序序列為cedbhjigfa,給出該二叉樹樹形表示。
答案:
9. 給定5個字元a~f,它們的權值集合W = {2, 3, 4, 7, 8, 9},試構造關于W的一棵哈夫曼樹,求其帶權路徑長度WPL和各個字元的哈夫曼樹編碼。
❝ 哈爾曼樹是帶權路徑長度最短的樹,權值較大的結點離根較近。
❞
❝ 哈夫曼樹的構造方法:首先統計出每種字元出現的頻率(也可以是機率)// 權值。第一步:找出字元中最小的兩個,小的在左邊,大的在右邊,組成二叉樹。在頻率表中删除此次找到的兩個數,并加入此次最小兩個數的頻率和。 點選了解詳解
❞
❝ 每個葉子到根的距離乘以葉子權值結果之和
❞
❝ 添加0和1,規則左0 右1。
❞
❝ 哈爾曼樹和編碼都不唯一的 隻有WPL才是唯一的
❞
答案:
其帶權路徑長度WPL = (9 + 7 + 8) * 2 + 4 * 3 + (2 + 3) * 4 = 80。
各個字元的哈夫曼樹編碼:a: 0000 b: 00001 c: 001 d: 10 e: 11 f:01 複制
10. 假設二叉樹中每個結點的值為單個字元,設計一個算法将一棵以二叉鍊方式存儲的二叉樹b轉換成對應的順序存儲結構a。
答案:
❝ 順序存儲結構:該結構是把邏輯上的相鄰的結點存儲在實體位置上相鄰的存儲單元中,結點之間的邏輯關系由存儲單元的鄰接關系來展現。
❞
❝ void: 函數沒有傳回值 那麼應聲明為void類型。
❞
設二叉樹的順序存儲結構類型為SqBTree,先将順序存儲結構a中所有元素置為'#'(表示空結點)。
将b轉換成a的遞歸模型如下
f(b, a, i) = a[i] = '#; 當b = NULL
f(b, a, i) = 由b結點data域值建立a[i]元素; 其他情況
f(b -> lchild, a, 2 * i);
f(b -> rchild, a, 2 * i + 1);
調用方式為:f(b, a, 1)(a的下标從1開始)。
void Ctree(BTNode *b, SqBtree a, int)
{
if(b != NULL) // 非空結點
{
a[i] = b -> data;
Ctree(b -> lchild, a, 2 * i);
Ctree(b -> rchild, a, 2 * i + 1);
}
else // 空節點
{
a[i] = '#';
}
} 複制
11. 假設二叉樹中每個結點值為單個字元,采用順序存儲結構存儲。設計一個算法,求二叉樹t中的葉子結點個數。
答案:
用i周遊所有的結點,當i大于等于MaxSize,傳回0。
當t[i]是空結點時傳回0;
當t[i]是非空結點時,若它為葉子結點,num增1;
否則遞歸調用num1 = LeftNode(t, 2 * t)求出左子樹的葉子結點個數num1,
再遞歸調用num2 = LeftNode(t, 2*i + 1)求出右子樹的葉子結點個數num2,
置num += num1 + num2。最後傳回num。
int LeftNode(SqBTree t, int i)
{
int num1,
num2,
num = 0;
if(i < MaxSize)
{
if(t[i] != '#') // 非空結點
{
if(t[2 * i] == '#' && t[2 * i + 1] == '#') // 葉子結點
{
num ++;
}
else
{
num1 = LeftNode(t, 2 * i);
num2 = LeftNode(t, 2 * i + 1);
num += num1 + num2;
}
return num;
}
else
{
retrun 0;
}
}
else
{
return 0;
}
} 複制
12. 假設二叉樹中每個結點值為單個字元,采用二叉樹鍊存儲結構存儲。設計一個算法計算給定二叉樹b中的所有單分支結點個數。
答案:
計算一棵二叉樹的所有單分支結點個數的遞歸模型f(b)如下:
f(b) = 0 若b = NULL;
f(b) = f(b -> lchild) + f(b -> rchild) + 1; 若b結點為單分支
f(b) = f(b -> lchild) + f(b -> rchild) 其他情況
int SSonNodes(BTNode *b)
{
int num1,
num2 ,
n;
if(b == NULL) // 空結點
{
return 0;
}
else if((b -> lchild == NULL && b -> rchild != NULL) || (b -> lchild != NULL && b -> rchild == NULL)) // 為單個分支結點
{
n = 1;
}
else
{
n = 0;
}
// 遞歸
num1 = SSonNodes(b -> lchild); // 遞歸求左子樹單分支結點數
num2 = SSonNodes(b -> rchild); // 遞歸求右子樹單分支結點數
return (num1 + num2 + n);
} 複制
13. 假設二叉樹中每個結點值為單個字元,采用二叉樹存儲結構存儲。設計一個算法求二叉樹b中最小值的結點值。
答案:
設f(b, min)是在二叉樹b中尋找最小結點值min,其遞歸模型如下
f(b, min) = 不做任何事件 // 若b = NULL
f(b, min) = 當b -> data < min時置min = b -> data; // 其他情況
f(b -> lchild, min);f(b -> rchild, min);
void FindMinNode(BTNode *b, char min)// void的作用:1.當函數不需要傳回值時,必須使用void限定 2. 當函數不允許接受參數時,必須使用void限定
{
if(b -> data < min) // 目前結點值比最小值小則置換
{
min = b -> data;
}
// 遞歸
FindMinNode(b -> lchild, min); // 在左子樹中找最小結點值
FindMinNode(b -> rchild, min); // 在右子樹中找最小結點值
}
void MinNode(BTNode *b) // 輸出最小結點值
{
if(b != NULL) // 非空結點
{
char min = b -> data; // char是容納單字元的一種基本資料類型
FindMinNode(b, min);
printf("Min = %c\n", min);
}
} 複制
14. 假設二叉樹每個結點值為單個字元,采用二叉樹存儲結構存儲。設計一個算法将二叉樹b1複制到二叉鍊b2中。
答案:
當b1為空時,置b2為空樹。
當b1不為空時,建立b2結點(b2為根結點),置b2 -> data = b1 -> data;
遞歸調用Copy(b1 -> lchild, b2 -> lchild),由b1的左子樹建立b2的左子樹;
遞歸調用Copy(b1 -> rchild, b2 -> rchild),由b1的右子樹建立b2的右子樹。
對應的算法如下:
void Copy(BTNode *b1, BTNode *&b2)
{
if(b1 == NULL)
{
b2 = NULL;
}
else
{
b2 = (BTNode *)malloc(sizeof(BTNode)); // malloc:動态配置設定 BTNode *:強制轉換為 sizeof(BTNode):為了擷取BTNode類型占據空間的大小
b2 -> data = b1 -> data;
// 遞歸
Copy(b1 -> lchild, b -> lchild);
Copy(b1 -> rchild, b -> rhcild);
}
} 複制
15. 假設二叉樹中每個結點值為單個字元,采用二叉鍊存儲結構存儲。設計一個算法,求二叉樹b中第K層上葉子結點個數。
答案:
采用先序周遊方法,當B為空時傳回0。置num為0。
若b不為空,目前結點的層次為K,并且b為葉子結點,則num增1,遞歸,
遞歸調用num1 = LevelkCount(b -> child, k, h+1)求出左子樹中第K層的結點個數num1,
遞歸調用num2=LevelKCount(b -> rchild, k, h + 1)求出右子樹中第K層的結點個數num2,
置num += num1 + num2,最後傳回num。
對應的算法如下
int LevelkCount(BTNode *b, int k, int h)
{
int num1,
num2,
num = 0;
if(b != NULL) // 非空結點
{
if(h == k && b -> lchild == NULL && b -> rchild == NULL) // 葉子結點
{
num ++;
}
// 遞歸
num1 = LevelkCount(b -> lchild, k, h + 1);
num = LevelkCOunt(b -> rchild, k, h + 1);
num += num1 + num2;
return num;
}
return 0;
}
int Levelkleft(BTNode *b, int k)
{
return LevelkCount(b, k, 1);
} 複制
16. 假設二叉樹中每個結點值為單個字元,采用二叉樹結構存儲。設計一個算法,判斷值為X的結點與值為Y的結點是否互為兄弟,假設這樣的結點值是唯一的。
答案:
采用先序周遊,當b為空時直接傳回false,
否則,若目前結點b是雙分支結點,且有互為兄弟的結點x丶y,則傳回true;
否則,遞歸調用flag=Brother(b->lchild, x, y),求出x丶y在左子樹是否互為兄弟,若flag為true,則傳回true;
否則遞歸調用Brother(b->rchild, x, y),求出x丶y在右子樹中是否互為兄弟,并傳回其結果。
對應的算法如下:
bool Brother(BTNode *b, char x, char y)
{
bool flag;
if(b == NULL)
{
return false;
}
else
{
if(b -> lchild != NULL && b -> rchild != NULL) // 左兄弟結點和
{
if((b -> lchild -> data === x && b -> rchild -> data == y))
{
return true;
}
// 遞歸
flag = Brother(b -> lchild, x, y);
if(flag == true)
{
return true;
}
else
{
return Brother(b -> rchild, x, y);
}
}
}
} 複制
17.假設二叉樹中每個結點值為單個字元,采用二叉鍊存儲結構存儲。設計一個算法,采用先序周遊方法求二叉樹b中值為x的結點的子孫,假設值為x的結點是唯一的。
答案:
設計Output(p)算法輸出以p為根結點的所有結點。
首先在二叉樹b中查找值為X的結點,目前b結點是這樣的結點,調用Output(b->lchild)輸出其左子樹中所有結點,調用Output(b->rchild)輸出其右子樹中所有結點,并傳回;
否則,遞歸調用Child(b->lchild, x)在左子樹中查找值為X的結點,遞歸調用Child(b->rchild, x)在右子樹中查找值為X的結點。對應的算法如下
void Output(BTNode *p)
{
if(p != NULL)
{
printf("%c", p -> data);
Output(p -> lchild);
Output(p -> rchild);
}
}
viod Child(BTNode *b, char x)
{
if(b != NULL)
{
// 找到為X的結點
if(b -> data == x)
{
if(b -> lchild != NULL)
{
Output(b -> lchild);
}
if(b -> rchild != NULL)
{
Output(b -> rchild);
}
return;
}
// 找不到為X的結點 則繼續遞歸
Child(b -> lchild, x);
Child(b -> rchild, x);
}
} 複制
18.假設二叉樹采用二叉樹存儲,設計一個算法把二叉樹b的左丶右子樹進行交換。要求不破壞原二叉樹。并用相關資料進行測試。
答案:
交換二叉樹的左丶右子樹遞歸模型如下:
f(b, t) = t = NULL 若b = NULL
f(b, t) = 複制根結點b産生結點t; 其他情況
f(b -> lchild, t1); f(b -> rchild, t2);
t -> lchild = t2; t -> rchild = t1
對應的算法如下(算法傳回左丶右子樹交換後的二叉樹)
#include "btree.cpp" // 二叉樹基本運算算法
BTNode *Swap(BTNode *b)
{
BTNode *t,
*t1,
*t2;
if(b == NULL)
{
t = NULL;
}
else
{
t = (BTNode *)malloc(sizeof(BTNode));
t -> data = b -> data; // 複制産生根結點t
t1 = Swap(b -> lchild);
t2 = Swap(b -> rchild);
t -> lchild = t2;
t -> rchild = t1;
}
return t;
}
// 或者設計成如下算法(算法産生左丶右子樹交換後的二叉樹b1)
vold Swap1(BTNode *b, BTNode *&b1)
{
if(b == NULL)
{
b1 = NULL;
}
else
{
b1 = (BTNode *)malloc(sizeof(BTNode));
b1 -> data = b -> data;
Swap1(b -> lchild, b1 -> rchild);
Swap1(b -> rchild, b1 -> lchild);
}
}
// 設計如下主函數
int main()
{
BTNode *b,
*b1;
CreateBTree(b, "A(B(D(G)), C(E, F))");
printf("交換前的二叉樹:");DispBTree(b);printf("\n");
b1 = Swap(b);
printf("交換後的二叉樹:");DispBTree(b1);printf("\n");
DestroyBTree(b);
DestroyBTree(b1);
return 1;
}
程式執行結果如下:
交換前的二叉樹:A(B(D(,G)), C(E, F));
交換後的二叉樹:A(C(F, E), B(, D, (G))) 複制
19.假設二叉樹采用二叉鍊式存儲結構,設計一個算法判斷一棵二叉樹b的左丶右子樹是否同構。
答案:
❝ 給定兩顆二叉樹T1和T2,如果T1可以通過若幹次左右孩子互換變成T2,則我們稱為兩顆二叉樹是同構的。
❞
判斷二叉樹b1丶b2是否同構的遞歸模型如下:
f(b1, b2) = true b1= b2 = NULL
f(b1, b2) = false 若b1丶b2中有一個為空,另一個不為空
f(b1, b2) = f(b1 -> lchild, b2 -> lchild) & f(b1 -> rchild, b2 -> rchild)
對應的算法如下
bool Symm(BTNode *b1, BTNode * b2) // 判斷二叉樹b1和b2是否同構
{
if(b1 == NULL && b2 == NULL)
{
return true;
}
else if(b1 == NULL || b2 == NULL)
{
return false;
}
else {
return (Symm(b1 -> lchild, b2 -> lchild) & Symm(b1 -> rchild, b2 -> rchild));
}
}
bool Symmtree(BTNode *b) // 判斷二叉樹的左丶右子樹是否同構
{
if(b == NULL)
{
return true;
}
else {
retrun Symm(b -> lchild, b -> rchild);
}
} 複制
20.假設二叉樹以二叉樹存儲,設計一個算法,判斷一棵二叉樹B是否為完全二叉樹。
答案:
根據完全二叉樹的定義,對完全二叉樹按照從上到下丶從左到右的次序周遊(層次周遊)應該滿足:
某結點沒有左孩子,則一定無右孩子
若某結點缺左或右孩子(一旦出現這種情況,置bj = false),則其所有後繼一定無孩子。
若不滿足上述如何一種,均不為完全二叉樹(cm = true表示是完全二叉樹,cm = false表示不是完全二叉樹)。
對應的算法如下:
bool CompBtree(BTNode *b)
{
BTNode *Qu(MaxSize), // 定義一個隊列,用于層次周遊
*p;
int front = 0, // 環形隊列的對頭指針
rear = 0; // 環形隊列的隊尾指針
bool cm = true; // cm為真表示二叉樹完全二叉樹
bool bj = true; // bj為真表示到目前為止所有結點均有左右孩子
if(b = NULL) // 空樹當成特殊的完全二叉樹
{
return true;
}
rear ++;
Qu[rear] = b; // 根結點進隊
while(front != rear) // 隊列不空
{
front = (fornt + 1) % MaxSize;
p = Qu[front]; // 出隊結點p
if(p -> lchild == NULL) // p結點沒有左孩子
{
bj = false; // 出現結點P缺失左孩子的情況
if(p -> rchild != NULL) // 沒有左孩子但有右孩子,違反(1)
{
cm = false;
}
}
else // p結點有左孩子
{
if(!bj) // bj為假而結點p還有左孩子,違反(2)
{
cm = false;
}
rear = (rear + 1) % MaxSize;
Qu[rear] = p -> lchild; // 左孩子進隊
if(p -> rchild == NULL)
{
bj = false; // 出現結點P缺失右孩子的情況
}
else
{
rear = (rear + 1) % MaXSize;
Qu[rear] = p -> rchild; // 将p結點的右孩子進隊
}
}
}
return cm;
} 複制
如果你看完覺得這篇文章不錯
- 關注公衆号【前端應屆生】,持續為你推送精彩文章。