線性回歸模型預測B站視訊點贊量與收藏量的關系(華農兄弟)
文章目錄
- 線性回歸模型預測B站視訊點贊量與收藏量的關系(華農兄弟)
- 前言
- 一、線性回歸模型
- 二、擷取資料
- 三、模型訓練
- 四、代碼
- 參考文獻
前言
線性回歸模型可以用來預測資料的走勢。通過對現有資料集的訓練,可以得到一個線型函數Y=w*X+b,通過這個線性函數可以預測出後續的值。
一、線性回歸模型
線型回歸是在假設目标值X與特征值Y有線型相關關系的前提下,通過已知的資料集對線性模型:
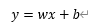
進行求解,具體的求解方式為建構損失函數,使得損失函數的值越來越小,直到達到精度要求或者是疊代次數要求。損失函數可以了解為在計算的過程種得到的預測值與真實值之間的差距,使得差距越小,模型就與真實值越相似。損失函數的定義:
要使得損失函數最小,對 Loss(w,b) 最小化。引入梯度下降算法,沿着梯度的方向下降的速度是最快的。每次疊代更新w和b,直到達到要求。
計算 Loss(w,b) 對于w和b的偏導數,分别為(可以将y=w*x+b導入到損失函數中):
二、擷取資料
爬取BILIBILI上的視訊資訊,本文擷取到“華農兄弟”的視訊資訊。可以參考部落格爬取B站UP的所有視訊細節資訊。取其中的視訊的點贊量和收藏量,對其建立線性回歸模型,預測其關系。視訊點贊量(x軸)與收藏量(y軸)的散點圖如下:
由于資料的集中性很差,需要對資料進行歸一化處理,本文使用最大最小值歸一化。
三、模型訓練
經過訓練得到w=0.7229486928307687 b=0.20322045504258518 訓練後的模型如下:
四、代碼
# 線型回歸模型預測B站視訊點贊量與收藏量的關系(華農兄弟)
import json
import numpy as np
import time
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
class LR(object):
def __init__(self, max_iterator = 1000, learn_rate = 0.01):
self.max_iterator = max_iterator
self.learn_rate = learn_rate
self.w = np.random.normal(1, 0.1)
self.b = np.random.normal(1, 0.1)
def cal_day(self, release_date, now_date):
# 計算天數
start_time = time.mktime(time.strptime(release_date.split(' ')[0], '%Y-%m-%d'))
end_time = time.mktime(time.strptime(now_date.split(' ')[0], '%Y-%m-%d'))
return int((end_time - start_time)/(24*60*60))
def load_data(self, url):
with open(url, 'r', encoding='utf-8') as f:
data_dect = json.load(f)
# print(data_dect)
# 視訊播放數量以及釋出距離現在的天數
watched_number_list = []
time_list = []
dm_number_list = []
liked_list = []
collected_list = []
for sample in data_dect:
# 去掉壞點
if sample['watched'] != '':
watched_number_list.append([float(sample['watched'])]) #觀看數量
liked_list.append([float(sample['liked'])]) #點贊數
collected_list.append([float(sample['collected'])]) #收藏數
dm_number_list.append([float(sample['bullet_comments'])]) #彈幕數
time_list.append([float(self.cal_day(sample['date'], sample['now_date']))]) #視訊釋出距離現在時間
return np.array(time_list), np.array(watched_number_list), np.array(liked_list), np.array(collected_list), np.array(dm_number_list)
def train_set_normalize(self, train_set):
data_range = np.max(train_set) - np.min(train_set)
return (train_set - np.min(train_set)) / data_range
def cal_gradient(self, x, y):
# 計算梯度
# print(x, y)
dw = np.mean((x * self.w + self.b - y) * x)
db = np.mean(self.b + x * self.w - y)
return dw, db
def train(self, x, y):
# 訓練模型,使用梯度下降
train_w = []
train_b = []
for i in range(self.max_iterator):
print(self.w, self.b)
train_w.append(self.w)
train_b.append(self.b)
i += 1
# 計算梯度值,向着梯度下降的方向
dw, db = self.cal_gradient(x, y)
self.w -= self.learn_rate*dw
self.b -= self.learn_rate*db
return train_w, train_b
def predict(self, x):
# 預測
return x * self.w + self.b
def myplot(self, x, y, train_w, train_b):
plt.pause(2)
plt.ion()
# 動态繪圖
for i in range(0, self.max_iterator, 30):
plt.clf()
# 原始散點圖
plt.scatter(x, y, marker = 'o',color = 'yellow', s = 40)
plt.xlabel('liked')
plt.ylabel('collected')
plt.plot(x, train_w[i] * x + train_b[i], c='red')
plt.title('step: %d learning-rate: %.2f function: y=%.2f * x + %.2f' %(i, self.learn_rate, train_w[i], train_b[i]))
plt.pause(0.5)
plt.show()
plt.ioff()
plt.pause(200)
lr = LR()
time_list, watched_number_list, liked_list, collected_list, dm_number_list = lr.load_data(r'2020\Crawl\Bilibili\Item1\data\video_detial.json')
# 需要對資料進行歸一化處理
tw, tb = lr.train(lr.train_set_normalize(liked_list), lr.train_set_normalize(collected_list))
lr.myplot(lr.train_set_normalize(liked_list), lr.train_set_normalize(collected_list), tw, tb)
參考文獻
- https://www.cnblogs.com/geo-will/p/10468253.html