統計學習：正則化與交叉驗證

1. 正則化

      模型選擇的經典方法是正則化（regularization）。正規化是結構風險最小化政策的實作，是在經驗風險上加一個正則化項（regularizer）或罰項（penalty term）。正則化一般是模型複雜度的單調遞增函數，模型越複雜，正則化值就越大。比如，正則化項可以是模型參數向量的範數。 正則化一般具有如下形式 

minfϵΓ1N∑i=1NL(yi,f(xi))+ΛJ(f)

      其中，第一項是經驗風險，第二項是正則化項，Λ≥0為調整兩者之間關系的系數。正則化項可以取不同的形式。例如。回歸問題中，損失函數是平方損失，正則化項可以是參數向量的L2範數：

L(w)=1N∑i=1N(f(xi,w)−y)2+Λ2∥w∥2

這裡，∥w∥表示參數向量w的L2範數。 

正則化項也可以是參數向量的L1範數： 

L(w)=1N∑i=1N(f(xi,w)−y)2+Λ2∥w∥1

這裡，∥w∥1表示參數向量w的L1範數。 

      第一項的經驗風險較小的模型可能較複雜（有多個非零參數），這時第二項的模型複雜度會較大。正則化的作用是選擇經驗風險與模型複雜度同時較小的模型。

     在所有可能選擇的模型中，能夠很好地解釋已知資料并且十分簡單才是最好的模型，也就是應該選擇的模型。從貝葉斯估計的角度來看，正則化項對應于模型的先驗機率。可以假設複雜的模型有較小的先驗機率，簡單的模型有較大的先驗機率。

　正則化項符合奧卡姆剃刀原理。奧卡姆剃刀原理應用于模型選擇時變為一下想法：在所有可能選擇的模型中，能夠很好地解釋已知資料并且十分簡單才是好模型。從貝葉斯估計的角度來看，正則化項對應于模型的先驗機率，可以假設複雜的模型有較小的先驗機率，簡單的模型有較大的先驗機率。正則化的本質就是，給優化參數一定限制。

　可能還是對為什麼正則化搞不清楚？舉個不是很恰當的例子：商家制作雨傘，我喜歡的是雨傘上有斑點狗團，材料要絲綢的，帶蕾絲邊的，還希望雨傘上能播放點小電影。。。。但是！！！我這個需求太特殊化了，除非我有錢請一個私人廠家為我量身定制。因為如果廠家把這樣的雨傘制作出來，别人估計不會買（對測試集未知資料沒有很好地誤差），這就叫過拟合。并且我的這些個性需求越多，那麼雨傘造價就越高。廠家要制作的是滿足大衆需求的，具有普遍共性的雨傘。這就是奧卡姆剃刀原理，保證了大衆需求的同時他又很簡單。正則化就是就好比加入了成本控制項目，它是個性需求複雜度的函數。

L0,L1,L2正則化（重點）

　　L0範數：向量中非0元素的個數。如果用L0範數來規則化一個參數矩陣W的話，那麼我們希望W的元素大部分都是0。讓參數是稀疏的。L0範數的最小化問題在實際應用中是NP難問題,是以在實際中不會應用。

　　L1範數是向量中各個元素絕對值之和，有個美稱“稀疏規則算子”，為什麼L1會使權值稀疏？L1範數是L0範數的最優凸近似。既然L0可以實作稀疏，為什麼不用L0，而要用L1呢？個人了解一是因為L0範數很難優化求解（NP難問題），二是L1範數是L0範數的最優凸近似，而且它比L0範數要容易優化求解。是以大家才把目光和萬千寵愛轉于L1範數。L1範數和L0範數可以實作稀疏，L1因具有比L0更好的優化求解特性而被廣泛應用。

　  參數稀疏的好處是什麼？

對稀疏趨之若鹜的一個關鍵原因就是它能實作特征的自動選擇。一般來說，樣本X的大部分内容（大部分特征）都是和最終的輸出y無關的或者不提供任何資訊。在經驗風險最小化的時候，考慮這些特征，雖然可以提高訓練誤差，但是在預測新的樣本時，這些沒用的資訊反而會被考慮，進而幹擾了正确的預測。稀疏規則算子就是為了完場特征自動選擇的光榮使命。它會将沒用的特征去掉，将這些特征對應的權重設定為0.

模型可解釋性強。

　　L2範數是指向量各元素的平方和然後求平方根。在回歸裡面，把有L2 範數的回歸稱為嶺回歸，有人也稱它為權值衰減。我們讓L2範數的規則項最小，可以使得W的每個元素都很小，都接近于0，但與L1範數不同，它不會讓它等于0，而是接近于0，這裡是有很大的差別的。而越小的參數說明模型越簡單，越簡單的模型則越不容易産生過拟合現象。實際上L2範數就是限制了權重參數的增長。

在經驗風險最小化的基礎上，加入了正則化項，相當于是加了限制條件，變成了有限制條件的最優化問題。

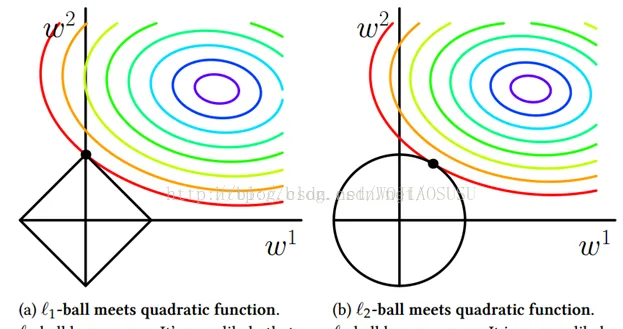
上面這幅圖很好的解釋了L1範數與L2範數

         L1範數：。L1的輸出圖像如上左圖所示，發現L1圖像在和每個坐标軸相交的地方都有角出現，而目标函數的等值線除非擺的非常好，否則大部分的時候都會在有角的地方相交。而在有角的地方相交會産生稀疏性。

         相比之下，L2沒有L1範數這樣的性質，因為沒有角，是以第一次相交的地方出現在具有稀疏性的地方可能性比較小。

即采用L1範數正則化項等值線與經驗風險等值線的交點常常出現自坐标軸上，即W1或者W2等于0，這樣就相當于減少了參數的數量。采用L2範數的時候，交點一般出現在某個象限内，即W1，W2均不為0,。換言之L1範數更易于得到稀疏解。

         W取得稀疏解意味着初始的d歌特征中僅僅對應的權重w不為0的特征才會出現在最終模型中，于是求解L1範數正則化的結果是得到了僅采用一部分初始特征的模型。L1範數的求解可以采用近端梯度下降PGD。

2. 交叉驗證

另一種常用的模型選擇方法是交叉驗證（cross validation） 

      如果給定的樣本資料充足，進行模型選擇的一種簡單方法是随機的降資料集分成：訓練集（training set）、驗證集（validation set）、測試集(test set)。訓練集用來訓練模型，驗證集用來選擇模型，測試集用于最終對學習方法的評估。在學習到的不同複雜度的模型中，選擇對驗證集有最小預測誤差的模型。由于驗證集有足夠多的資料，用它對模型進行選擇也是有效的。

     但是在實際應用中資料時不充足的。為了選擇好的模型，可以采用交叉驗證方法。交叉驗證的基本思想：重複的使用資料；把給定的資料進行切分，将切分的資料集組合為訓練集與測試集，在此基礎上反複的進行訓練、測試及模型選擇。

1. 簡單交叉驗證

   方法：首先随機的将已給資料分為兩部分，一部分作為訓練集，另一部分作為測試集（例如70%作為訓練，30%作為測試），然後用訓練集在各種條件下（不同的參數個數）訓練模型，進而得到不同的模型；在訓練集上評價各個模型的測試誤差，選出測試誤差最小的模型。

2. S折交叉驗證（ 應用最多）

   方法：首先随機的将已給資料切分為S個互不相交的大小相同的自己；然後利用S-1個自己的資料訓練模型，利用餘下的子集測試模型；将這一過程對可能的S種選擇重複進行；最後選出S次評測中平均測試誤差最小的模型。

3. 留一交叉驗證

   S折交叉驗證的特殊情形是S=N，稱為留一交叉驗證（leave-one-out cross validation），往往在資料缺乏的情況下使用。這裡，N是給定資料集的容量。