在上一期内容中,我們介紹了當考察一個疾病預測模型好壞的時候,常常會關注到2個次元,一個是預測模型的區分度(Discrimination),它反映了該模型是否能夠将患者和非患者區分開來的能力;另一個次元是預測模型的校準度(Calibration),它反映了該模型預測結果與實際情況的符合程度。 (點選檢視: 你的預測模型靠譜嗎?詳解區分度和校準度的SPSS操作! ) 那麼對于兩個疾病風險預測模型,應該選用哪一個模型更靠譜呢,應該 如何比較兩個疾病模型的預測能力呢? 本期内容小咖就來向大家介紹一個老朋友 AUC 和一個新朋友 NRI 。
ROC曲線及其AUC
首先我們來複習一下ROC曲線,在診斷試驗中,通常根據檢驗名額的判斷結果和金标準診斷結果,整理成一個2×2的表格,如下表所示,并以此來計算診斷試驗中兩個比較重要的名額,即靈敏度和特異度。(戳連結:評價診斷試驗的兩大名額,你都搞清楚了嗎?)
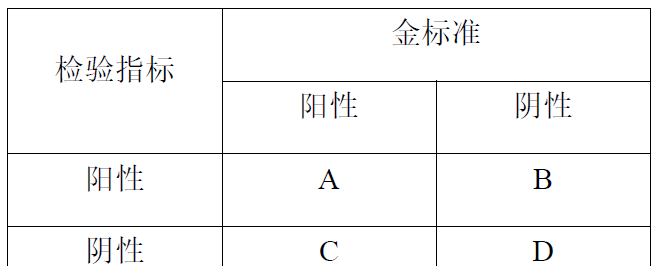
靈敏度=A/(A+C),即真陽性率,反映了将實際有病的人正确地判定為陽性的比例。
特異度=D/(B+D),即真陰性率,反映了将實際無病的人正确地判定為陰性的比例。
如果檢驗名額為連續性變量,我們可以将該檢驗名額劃分為不同的切點,切點以上判斷為陽性,切點以下判斷為陰性,每個切點下都對應一個靈敏度和特異度,然後以靈敏度為縱坐标,1-特異度為橫坐标繪制圖形,即可得到我們熟悉的受試者工作特征曲線(Receiver Operating Characteristic curve,ROC曲線)。
從ROC曲線可以看出,随着靈敏度的上升,1-特異度增加,即特異度下降,反之亦然,當滿足靈敏度和特異度相對最優時,可以把位于ROC曲線左上角的切點,作為适宜的診斷界值,即下圖中的y點。同時,為了評價該檢驗名額的診斷能力,可以進一步計算曲線下面積(Area Under the Curve,AUC),AUC越大,提示名額的診斷能力越好。
除了應用在經典的診斷試驗中,通常在建構好一個疾病預測模型後,ROC曲線及其AUC也可以延伸到用來對疾病預測模型的預測能力進行評估和判斷。
當兩個不同預測模型之間進行比較時,AUC越大,則提示模型對疾病發生機率的預測能力越好(戳連結:咋評價疾病預測模型?又見到熟悉的ROC曲線)。兩個模型之間的AUC比較采用Z檢驗,統計量Z近似服從正态分布,計算公式如下:
其中SE1和SE2分别為AUC1和AUC2的标準誤。
雖然ROC曲線及其對應的AUC已經在疾病預測模型的評價中得到了廣泛的應用,但是由于計算AUC時綜合了ROC曲線上所有點作為界值時的情況,而在實際的臨床應用中,我們通常隻會選取一個适宜的診斷切點,關心在這個切點下的診斷能力,而非所有點組成的曲線下面積。
同時,當我們在比較兩個模型的預測能力時,特别是想要比較在模型中引入新的名額後,模型的預測能力是否有所提高,此時新加入的名額有時很難顯著改善AUC,AUC的增量并不明顯,其意義也不容易了解。在這種情況下,我們就需要用到另一個比較兩個模型預測能力的名額——淨重新分類指數(Net Reclassification Index,NRI)。
淨重新分類指數NRI
相對于ROC曲線及其AUC,NRI更關注在某個設定的切點處,兩個模型把研究對象進行正确分類的數量上的變化,常用來比較兩個模型預測能力的準确性。
簡單的說,首先舊模型會把研究對象分類為患者和非患者,然後在舊模型的基礎上引入新的名額構成新模型,新模型會把研究對象再重新分類成患者和非患者。
此時比較新、舊模型對于研究人群的分類變化,就會發現有一部分研究對象,原本在舊模型中被錯分,但在新模型中得到了糾正,分入了正确的分組,同樣也有一部分研究對象,原本在舊模型中分類正确,但在新模型中卻被錯分,是以研究對象的分類在新、舊模型中會發生一定的變化,我們利用這種重新分類的現象,來計算淨重新分類指數NRI。
那麼如何計算NRI值呢,方法其實也很簡單。首先我們将研究對象按照真實的患病情況分為兩組,即患者組和非患者組,然後分别在這兩個分組下,根據新、舊模型的預測分類結果,整理成兩個2×2的表格,如下表所示。
我們主要關注被重新分類的研究對象,從表中可以看出,在患者組(總數為N1),新模型分類正确而舊模型分類錯誤的有B1個人,新模型分類錯誤而舊模型分類正确的有C1個人,那麼新模型相對于舊模型來說,正确分類提高的比例為(B1-C1) / N1,即對角線以上的比例-對角線以下的比例。
同理,在非患者組(總數為N2),新模型分類正确而舊模型分類錯誤的有C2個人,新模型分類錯誤而舊模型分類正确的有B2個人,那麼新模型相對于舊模型正确分類提高的比例為(C2-B2) / N2,即對角線以下的比例-對角線以上的比例。
最後,綜合患者組和非患者組的結果,新模型與舊模型相比,淨重新分類指數NRI= (B1-C1) / N1+(C2-B2) / N2
若NRI>0,則為正改善,說明新模型比舊模型的預測能力有所改善;若NRI<0,則為負改善,新模型預測能力下降;若NRI=0,則認為新模型沒有改善。我們可以通過計算Z統計量,來判斷NRI與0相比是否具有統計學顯著性,統計量Z近似服從正态分布,公式如下:
進一步将NRI的公式推導可以得出:
NRI =(靈敏度new - 靈敏度old)+(特異度new - 特異度old)=(靈敏度new + 特異度new)-(靈敏度old + 特異度old)
問題就轉化為我們熟悉的靈敏度和特異度這兩個名額了。我們在前期推送的文章中《如何比較兩種方法的靈敏度和特異度?來看執行個體教程!》,讨論過這種複雜的情況:
如果靈敏度new >靈敏度old,特異度new >特異度old,此時可認為新模型優于舊模型,相當于這裡的NRI >0;
如果靈敏度new < 靈敏度old,特異度new < 特異度old,此時可認為新模型劣于舊模型,相當于這裡的NRI <0;
如果新模型和舊模型的靈敏度和特異度具有差異,但方向不一緻時,就需要用到約登指數(靈敏度+特異度-1)來進行判斷,而此時NRI就相當于新模型和舊模型的約登指數的內插補點,是以NRI在比較兩個模型預測能力時更具有綜合性。
研究執行個體1
如果還是不明覺厲,沒關系,我們通過模拟一個研究執行個體,來向大家介紹如何在實際的研究中計算NRI。假設某研究納入的樣本中有患者180例,非患者415例,研究者拟評價,在舊模型的基礎上加入新的生物标志物後,新模型預測能力的改善情況。
在本研究180例患者組中,舊模型預測陽性148人中有8人被新模型錯分到陰性,舊模型預測陰性32人中有30人被新模型重新正确分到陽性組。而在415例非患者中,舊模型預測陰性360人中有15人被新模型錯分到陽性,舊模型預測陽性55人中有32人被新模型重新正确分到陰性組,資料整理為如下表格。
根據上述NRI公式計算如下:
NRI= (B1-C1) / N1+(C2-B2) / N2=(30-8)/180+(32-15)/415=16.3%
Z=4.292,P<0.001,具有統計學顯著性,提示在加入了新的生物标志物後,新模型的預測能力有所改善,正确分類的比例提高了16.3%。
研究執行個體2
在第一個例子中,我們設定的結局變量為是否患病的二分類變量,但在有些情況下,直接根據預測模型判斷是否患病顯得過于絕對,預測模型給出的是未來患病的機率值,研究人員可能更關注的是患病風險的大小,例如将研究對象根據預測的風險機率劃分為高、中、低三組,由此可以采取不同的幹預措施。
針對此時結局變量是3分類或者更多分類時,ROC曲線呈現出一個球面的形狀,繪制起來比較困難,更無法直覺的去比較兩個預測模型的AUC了,而NRI卻可以很好的解決這個問題,這也是我們在實際分析中最常用到NRI的地方。
我們結合一篇2008年發表在Stat Med雜志上的文章為例,《Evaluating the added predictive ability of a new marker: from area under the ROC curve to reclassification and beyond》,研究者以著名的Framingham Heart Study為基礎,比較了在經典的模型中加入HDL-C名額後,新模型對于研究對象未來10年冠心病發病風險預測能力的改善情況。
研究人員首先比較了新、舊模型的ROC曲線,結果顯示新、舊模型AUC分别為0.774和0.762,加入HDL-C後新預測模型AUC增加了0.012,差異無統計學顯著性(P=0.092),提示新模型并無顯著改善。
随後,研究人員又進一步将研究對象未來10年發生冠心病事件的風險機率,按照<6%,6-20%,>20%分為低、中、高三組,并計算了NRI,資料格式如下:
根據上述NRI公式,我們可以計算出:
NRI=[(15+0+14)-(4+0+3)]/183+[(148+1+25)-(142+0+31)]/3081=12.1%
Z=3.616,P<0.001,具有統計學顯著性,提示在加入了新的生物标志物後,新模型的預測能力有所改善,正确分類的比例提高了12.1%。
由此可以看出,當兩個模型的AUC差異比較無統計學顯著性時,提示模型的區分能力(Discrimination)相近,但是進一步計算NRI後就會發現,新模型正确再分的能力(Reclassification)有顯著提高,是以需要我們将AUC和NRI綜合起來進行判斷。
參考文獻:
[1] Stat Med. 2008 Jan 30;27(2):157-72.
醫咖會專欄課程《缺失值的處理和常見研究類型的統計分析》!
講解缺失資料的核心處理方法及SPSS操作,以及病例對照研究和RCT的統計分析思路。
使用電腦,打開醫咖會,觀看專欄視訊:
https://www.mediecogroup.com/zhuanlan/courses/7
關注醫咖會,及時擷取最新統計教程
點選左下角“”,檢視全部免費統計教程。或者使用電腦打開網址:http://www.mediecogroup.com/,分類檢視全部統計教程。
快加小咖個人微信(xys2019ykh),拉你進統計讨論群和衆多熱愛研究的小夥伴們一起交流學習。