前言
最近因為要做一個預測性的工程進而學到了邏輯回歸(Logistic Regression),看了很多的資料以及一些論壇上的博文,發現了很多不錯的資料,也發現了一些不足甚至是錯誤的地方。是以,在這裡我重新從自己的視角以及了解寫一下我對邏輯回歸的認識,糾正一些科普資料中的錯誤,再加上自己的學習過程。
如果有錯誤或者不足的地方歡迎看到的人批評指正,互相交流。
原理及用途
回歸從表現出形式上講就是給定一些點集,找出一條曲線去拟合。從數學公式的角度講,就是在已經大概知道函數形式的時候,用給出的訓練樣本确定函數中未知的參數。是以在進行回歸時,根據已有經驗找到一個合适形式的預測函數非常重要。假如說預測函數的分布是非線性的,而我們選擇了一個線性函數來預測,就會造成較大的偏差。其實邏輯回歸就是線上性回歸的基礎上加了一個邏輯函數,但是這個邏輯函數非常重要,造就了邏輯回歸在分類問題中的重要地位。
邏輯回歸經常應用于分類問題,特别是“二分類”。就是預測結果隻有兩種“0”或者“1”。具體的用途有:
- 分析行為:根據某人的行為習慣分析使用者某個行為會不會發生。
- 判斷預測:根據建立的模型,分析在某些自變量集合下,是否會發生某種疾病。
實作步驟
- 首先是找到一個合适形式的預測函數,稱為 hθ 函數,即hypothesis。
- 構造損失函數,主要分為(1)0-1損失函數,稱為Cost函數,(2)平方損失函數,稱為 j(θ) 。
- j(θ) 函數的值越小表示預測的函數越準确,是以用logistic regression的方法求出 j(θ) 取最小值時函數的參數 θ 。
具體實作
構造預測函數
由于是“二分類”問題,是以這裡要用到Logistic函數,也叫做Sigmoid函數,函數的形式為
g(z)=11+e−z
Sigmoid函數的推導過程是:令 y=logp1−p
y=log(p/(1−p))⇔ey=p/(1−p)⇔ey=p+eyp⇔p=ey1+ey⇔p=11+e−y
該函數對應的圖像是:
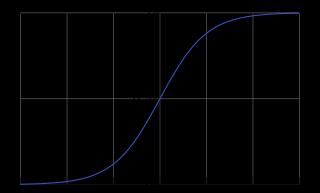
從圖像可以看出p在[0,1]之間,在解決二分類問題的時候可以設定一個門檻值,當p>門檻值的時候分為類别A,當P<門檻值的時候分為類别B。
推理過程
下面分析一下可能會遇到的問題,然後分析預測函數h的形式:
線性邊界:
首先以線性邊界的情況來讨論,線性邊界的邊界形式為:
θ0+θ1x1+⋯+θnxn=∑i=0nθixi=θTx
構造預測函數 hθ :
hθ=g(θTx)=11+e−θTx
hθ 表示預測結果取1的機率,那麼預測結果取0的機率可以表示為 1−hθ :
P(y=1|x;θ)=hθ(x)P(y=0|x;θ)=1−hθ(x)
該式還可以寫成 P(y|x;θ)=(hθ(x))y(1−hθ(x))1−y 。
使用最大似然估計:
L(θ)=∏i=1m(hθ(x(i)))y(i)(1−hθ(x(i)))1−y(i)
兩邊同時取對數:
l(θ)=logL(θ)=∑i=1m(y(i)hθ(x(i))+(1−y(i))(1−hθ(x(i))))
當 l(θ) 取得最大值時的 θ 就是最佳的 θ 的取值。
根據上式構造0-1損失函數和平方損失函數:
Cost(hθ(x),y)={−loghθ(x)−log(1−hθ(x))y=1y=0
J(θ)=1m∑i=1m(Cost(hθ(x(i))),y(i))=−1m∑i=1m(y(i)loghθ(x(i))+(1−y(i))(1−log(1−hθ(x(i))))
J(θ)=−1ml(θ) ,是以求 l(θ) 的最大值就是求 J(θ) 的最小值。
在這裡使用梯度下降的方法求 J(θ) 的最小值,關于梯度下降的介紹見,梯度下降是一個不斷地疊代求最小值的方法。簡單的形容就是:
WantminθJ(θ)Repeat{θj:=θj−α∂∂θjj(θ)}
其中 θj:=θj−α∂∂θjJ(θ) 就是梯度下降法的公式, θj: 是 θj 經過疊代後的下一次狀态。整個疊代過程終止的條件是 ∂∂θjJ(θ) 的結果趨近于0。
化簡 ∂∂θjJ(θ) :
∂∂θjJ(θ)=−1m∑i=1m[y(i)1hθ(x(i))∂∂θjhθ(x(i))−(1−y(i))11−hθ(x(i))∂∂θjhθ(x(i))]=−1m∑i=1m(y(i)1g(θTx(i))−(1−y(i))11−g(θTx(i)))∂∂θjg(θTx(i))=−1m∑i=1m(y(i)1g(θTx(i))−(1−y(i))11−g(θTx(i)))g(θTx(i))(1−g(θTx(i)))∂∂θj(θTx(i))=−1m∑i=1my(i)(1−g(θTx(i)))−(1−y(i))g(θTx(i))g(θTx(i))(1−g(θTx(i)))g(θTx(i))(1−g(θTx(i)))∂∂θjθTx(i)(j)=−1m∑i=1m(y(i)−g(θTx(i)))x(i)(j)=1m∑i=1m(hθ(x(i))−y(i))x(i)(j)
上述過程都屬于微積分中求偏導的過程,不熟悉的可以再看下微積分的知識。
求偏導過程中要用到的知識:
h(x)∂∂xh(x)=11+eg(x)=1(1+eg(x))2eg(x)∂∂xg(x)=h(x)(1−h(x))∂∂xg(x)
因為 α 是一個常數,是以 α1m 仍然是一個常數,是以式中的 1m 可以省略。是以 θj:=θj−α∂∂θjJ(θ) 可以化簡為:
θj:=θj−α∑i=1m(hθ(x(i))−y(i))x(i)(j);(j=0,1,…,n)
上式就是梯度下降法求解的最終公式:
WantminθJ(θ)Repeat{θj:=θj−α∑i=1m(hθ(x(i))−y(i))x(i)(j))}
對于訓練樣本:
X=⎡⎣⎢⎢⎢⎢⎢⎢x(1)0x(2)0⋮x(m)0x(1)1x(2)1⋮x(m)1……⋮…x(1)nx(2)n⋮x(m)n⎤⎦⎥⎥⎥⎥⎥⎥,Y=⎡⎣⎢⎢⎢⎢⎢y(1)y(2)⋮y(m)⎤⎦⎥⎥⎥⎥⎥
可以求出 θ 的值:
⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪θ0=θ0−α∑mi=1(hθ(x(i))−y(i))x(i)(0))θ1=θ1−α∑mi=1(hθ(x(i))−y(i))x(i)(1))……………………θm=θm−α∑mi=1(hθ(x(i))−y(i))x(i)(m))
至此邏輯回歸過程結束。
對于具體的訓練樣本資料,邏輯回歸所起到的作用如表所示:
| 資料 | 分類 | 預測結果1 | 分類結果1 | 預測結果2 | 分類結果2 |
|---|---|---|---|---|---|
| 10 | 1 | 1 | 1 | 0.1 | |
| 9 | 1 | 0.9 | 1 | 0.9 | 1 |
| 8 | 1 | 0.8 | 1 | 0.8 | 1 |
| 7 | 1 | 0.7 | 1 | 0.7 | 1 |
| 6 | 1 | 0.5 | 0.6 | 1 | |
| 5 | 0.6 | 1 | 0.5 | ||
| 4 | 0.4 | 0.4 | |||
| 3 | 0.3 | 0.3 | |||
| 2 | 0.2 | 0.2 | |||
| 1 | 0.1 | 1 | 1 |
并且可以看出訓練結果1的效果要好于訓練結果2。
代碼實作
import matplotlib.pyplot as plt
from numpy import *
def loadDataSet():
dataMat = []; labelMat = []
fr = open(r'C:\Users\crystal\Desktop\testSet-LR.txt')
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([, float(lineArr[]), float(lineArr[])])
labelMat.append(int(lineArr[]))
return dataMat,labelMat
def sigmoid(inX):
return /(+exp(-inX))
def gradAscent(dataMatIn, classLabels):
dataMatrix = mat(dataMatIn) #convert to NumPy matrix
labelMat = mat(classLabels).transpose() #convert to NumPy matrix
m,n = shape(dataMatrix)
alpha =
maxCycles =
weights = ones((n,))
for k in range(maxCycles): #heavy on matrix operations
h = sigmoid(dataMatrix*weights) #matrix mult
error = (labelMat - h) #vector subtraction
weights = weights + alpha * dataMatrix.transpose()* error #matrix mult
return weights
def GetResult():
dataMat,labelMat=loadDataSet()
weights=gradAscent(dataMat,labelMat)
print (weights)
plotBestFit(weights)
def plotBestFit(weights):
dataMat,labelMat=loadDataSet()
dataArr = array(dataMat)
n = shape(dataArr)[]
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
for i in range(n):
if int(labelMat[i])== :
xcord1.append(dataArr[i,]); ycord1.append(dataArr[i,])
else:
xcord2.append(dataArr[i,]); ycord2.append(dataArr[i,])
fig = plt.figure()
ax = fig.add_subplot()
ax.scatter(xcord1, ycord1, s=, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=, c='green')
x = arange(-, , )
y=(*x+)/()
# y = (-weights[0]-weights[1]*x)/weights[2]
ax.plot(x,y)
plt.xlabel('X1'); plt.ylabel('X2');
plt.show()
if __name__=='__main__':
GetResult()
訓練結果
參考資料:
1.http://www.360doc.com/content/14/0912/08/14875906_408823529.shtml
2.http://blog.csdn.net/pakko/article/details/37878837
3.http://blog.csdn.net/dongtingzhizi/article/details/15962797
4.http://blog.csdn.net/abcjennifer/article/details/7716281
5.http://blog.csdn.net/woxincd/article/details/7040944