資料降維的方法:
Manifold Learning(流行學習)
1、什麼是流形
流形學習的觀點:認為我們所能觀察到的資料實際上是由一個低維流行映射到高維空間的。由于資料内部特征的限制,一些高維中的資料會産生次元上的備援,實際上這些資料隻要比較低的次元就能唯一的表示。是以直覺上來講,一個流形好比是一個d維的空間,在一個m維的空間中(m>d)被扭曲之後的結果。需要注意的是流形并不是一個形狀,而是一個空間。舉個例子來說,比如說一塊布,可以把它看成一個二維的平面,這是一個二維的空間,現在我們把它扭一扭(三維空間),它就變成了一個流形,當然不扭的時候,它也是一個流形,歐式空間是流形的一種特殊情況。如下圖所示
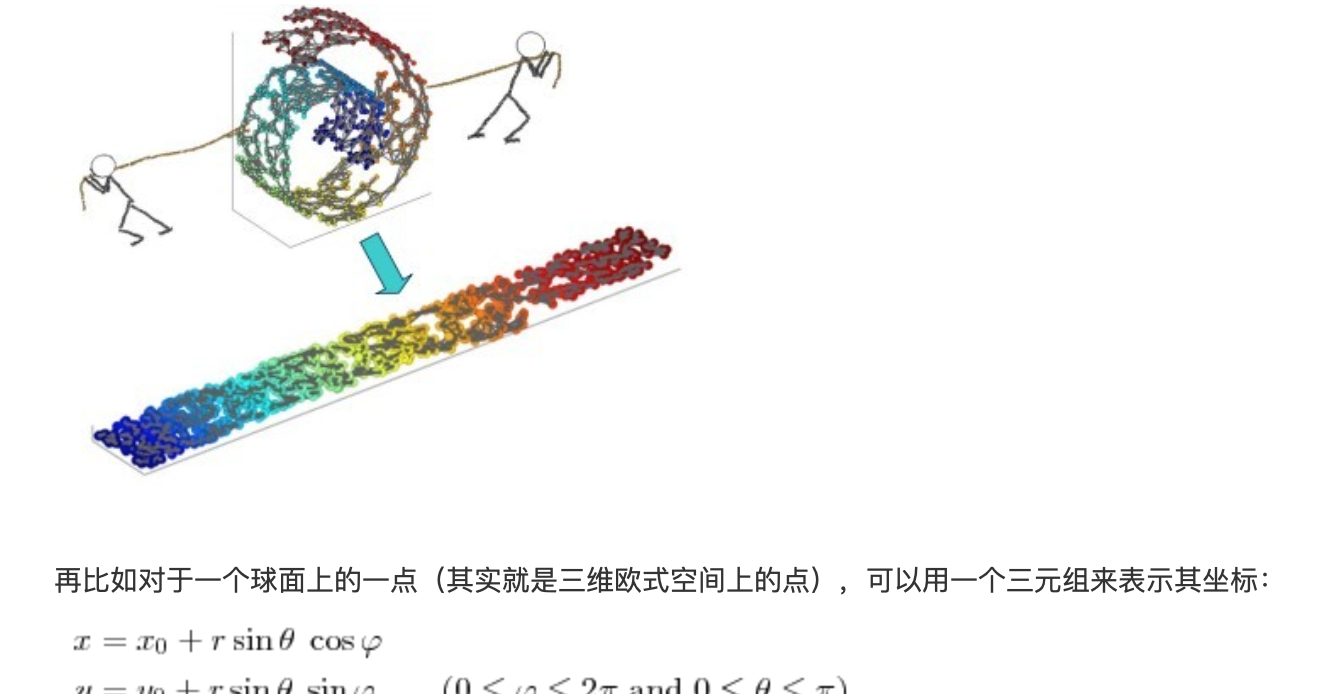
流形具有在局部與歐式空間同胚的空間,也就是它在局部具有歐式空間的性質,能用歐式距離來進行距離計算。這就給降維帶來了很大的啟發,若低維流形嵌入到了高維空間,此時樣本在高維空間的分布雖然複雜,但在局部上仍具有歐式空間的性質,是以可以在局部建立降維映射關系,然後再設法将局部映射關系推廣到全局。而且當資料被降維到二維和三維時,就可以進行可視化,是以流形學習也可以被用于可視化。
[1]Locally Linear Embedding(LLE)局部線性嵌入
局部線性嵌入的思想:隻是試圖去保持領域内樣本之間的關系。具體如下圖所示,樣本從高維空間映射到低維空間後,各個領域内的樣本之間的線性關系不變。
1)求最小值的Wij,固定住Wij,第一步根據鄰域關系計算出所有的樣本的領域重構系數w,也就是找出每一個樣本和其領域内的樣本之間的線性關系
2)在另外一個空間找到同樣Wij關系的兩個Zi,Zj,第二步就是根據領域重構系數不變,去求每個樣本在低維空間的坐标
2)zai
[2]Laplacian Eigenmaps
1)找一個graph,去降低次元的方法
問題:
高維的點做成低維的點,完成低維的可視化
降維前做相似度分析P
降維後做相似度分析Q
KL計算兩個分布的相近程度
計算機率的方法:兩個評估的方式:SNE tSNE tSNE更好的可視化,放大gap
LLE算法總結:
主要優點:
1)可以學習任意維的局部線性的低維流形。
2)算法歸結為稀疏矩陣特征分解,計算複雜度相對較小,實作容易。
3)可以處理非線性的資料,能進行非線性降維。
主要缺點:
1)算法所學習的流形隻能是不閉合的,且樣本集是稠密的。
2)算法對最近鄰樣本數的選擇敏感,不同的最近鄰數對最後的降維結果有很大影響。