svd是現在比較常見的算法之一,也是資料挖掘工程師、算法工程師必備的技能之一,這邊就來看一下svd的思想,svd的重寫,svd的應用。
這邊着重的看一下推薦算法中的使用,其實在圖檔壓縮,特征壓縮的工程中,svd也有着非常不凡的作用。
svd的思想
1.矩陣因子模型(潛在因子模型)
假設,我們現在有一個使用者u對商品i的程度矩陣,浏覽是1,搜尋是2,加車是3,下單是4,付款是5:
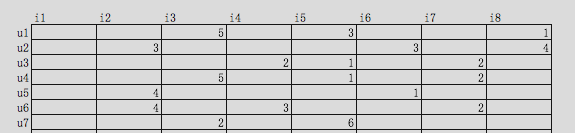
使用者商品矩陣
實際情況下,使用者不可能什麼商品都買,是以,該矩陣必然是一個稀疏矩陣,任意一個矩陣必然可以被分解成2個矩陣的乘積:
k就是潛在因子的個數,舉個例子,你去買衣服,你可能買了裙子,露背裝,我去買衣服,我買了牛仔褲,潮牌T恤,影響我們購買商品的差異的原因可能有很多點,但是必然有些原因占比重要些,比如性别,收入,有一些可能不那麼重要比如天氣,心情。而拆分成的Pu矩陣表示了這些潛在因子對我或者你的影響程度,Qi矩陣表示了各種商品對這些潛在因子的影響程度。
當我們盡可能的通過拆分矩陣的形式,目标使得拆分後的兩個矩陣的乘積最比對最上方的使用者商品矩陣的已知的資料值,進而可以通過這兩個矩陣的乘積填補掉空缺的值。
2.Baseline Predictors
這個是08年的,Koren在NetFlix大賽的一個思路,後續也延伸了svd多種變種,比如Asvd,有偏的Rsvd,對偶算法下的Svd++,這些算法的核心在于解決了Svd上面我們提到的那個矩陣龐大稀疏的問題,後續我們再看。
Baseline Predictors使用向量bi表示電影i的評分相對于平均評分的偏差,向量bu表示使用者u做出的評分相對于平均評分的偏差,将平均評分記做μ。
新的得分計算方式如下:Rui=μ+bi+bu
準備引入了商品及使用者的實際分布的情況,有效的降低在測試資料上面的效果。
3.svd數學原理
首先,線代或者高等代數裡面告訴我們:一個向量可以通過左乘一個矩陣的方式來進行拉伸,旋轉,或者同時拉伸旋轉。
是以,無論什麼矩陣M,我們都可以找到一組正交基v1、v2,使得Mv1、Mv2也是正交的,不妨記其方向為為μ1、μ2。
Mv1=δ1u1;
Mv2=δ2u2;
存在向量x,在v1、v2空間裡的表示為:x=(x·v1)v1+(x·v2)v2,
是以有,Mx有:
Mx=(x·v1)Mv1+(x·v2)Mv2
Mx=(x·v1)δ1u1+(x·v2)δ2u2
Mx=δ1u1(v1.T)x+δ2u2(v2.T)x
M=δ1u1(v1.T)+δ2u2(v2.T)
是以就有了那個非常有名的公式:
M=UΣV.T
U是有一組正交基構成的,V也是有一組正交基構成的,Σ是由δ1、δ2構成的,幾何意義上來說,M的作用就是把一個向量由V的正交空間變換到U的正交空間上,而通過Σ的大小來控制縮放的力度。
我們還需要知道一些簡單的推論,
- 通過MM.T,我們知道,δ的平方是MM.T的特征值
- 奇異值δ的數量決定了M=UΣV.T的複雜度,而奇異值的大小變化差異程度很大,通常前幾個奇異值的平方就能占到全部奇異值的平方的90%,是以,我們可以通過控制奇異值的數量來優化原始矩陣乘積,去除掉一下噪聲資料
svd重寫
基礎的svd
首先,我們在剛開始就知道,評分矩陣R可以用兩個矩陣P和Q的乘積來表示:
其中,U表示使用者數,I表示商品數,K=就是潛在因子個數。
首先通過那些已知的資料比如下方紅色區域内的資料去訓練這兩個乘積矩陣:
那麼未知的評分也就可以用P的某一行乘上Q的某一列得到了:
這是預測使用者u對商品i的評分,它等于P矩陣的第u行乘上Q矩陣的第i列。這個是最基本的SVD算法,下面我們們來看如何确定Pu、Qi:
假設已知的評分為:rui則真實值與預測值的誤差為:
繼而可以計算出總的誤差平方和:
隻要通過訓練把SSE降到最小那麼P、Q就能最好地拟合R了。正常的來講,梯度下降是非常好的求解方式,常見的包括随機梯度下降,批量梯度下降。
随機梯度下降一定程度會避免局部最小但是計算量大,批量梯度計算量小但是會存在鞍點計算誤區的問題。
先求得SSE在Puk變量(也就是P矩陣的第u行第k列的值)處的梯度:
現在得到了目标函數在Puk處的梯度了,那麼按照梯度下降法,将Puk往負梯度方向變化。令更新的步長(也就是學習速率)為
則Puk的更新式為
同樣的方式可得到Qik的更新式為
Rsvd
很明顯,上述這樣去求的矩陣QP必然會存在過度拟合的問題,導緻對實際資料預測的時候,效果遠差于訓練資料,仿造elastic net的思維:
對所有的變量就加入正則懲罰項,重新計算上面的梯度如下:
這就是正則svd,也叫做Rsvd,也是我們用的比較多的svd的方法。
偏移Rsvd
在最開始講了,Koren在NetFlix大賽裡面除了考慮了對原始資料的拟合情況,也考慮了使用者的評分、商品的平均得分相對于整體資料的偏移情況,有了新的得分公式:Rui=μ+bi+bu,影響的隻有eui,後面的Pu、qi的正則不受影響,但是新增了bi、bu的正則項,重新計算每一項的偏導數:
bu、bi的更新式子:
其餘的都不發生改變,這就叫做有偏移下的Rsvd
無論是Rsvd還是有偏移的Rsvd,當原始的使用者對商品的評分矩陣過大,比如有3億使用者,3億商品,形成9億商品集合的時候,這就是一個比較不可能完成的存儲任務,而且裡面絕大多數都是0的稀疏矩陣。
Asvd及Svd++
這邊,我們引入兩個集合:R(u)表示使用者u評過分的商品集合,N(u)表示使用者u浏覽過但沒有評過分的商品集合,Xj和Yj是商品的屬性。
Asvd的rui的評分方式:
Svd++的rui的評分方式:
無論是Asvd還是Svd++,都幹掉了原來龐大的P矩陣,取而代之的是兩個使用者浏覽評分矩陣大大縮小了存儲的空間,但是随着而來的是一大把更多的未知參數及疊代的複雜程度,所有在訓練時間上而言,會大大的增加。
我這邊隻重寫了一下Rsvd的python版本,網上挺多版本的疊代條件有一定問題,稍作處理了一下,并寫成了函數,大家可以參考一下:
def svd(mat, feature, steps=2000, gama=0.02, lamda=0.3):
#feature是潛在因子的數量,mat為評分矩陣
slowRate = 0.99
preRmse = 0.0000000000001
nowRmse = 0.0
user_feature = matrix(numpy.random.rand(mat.shape[0], feature))
item_feature = matrix(numpy.random.rand(mat.shape[1], feature))
for step in range(steps):
rmse = 0.0
n = 0
for u in range(mat.shape[0]):
for i in range(mat.shape[1]):
if not numpy.isnan(mat[u,i]):
#這邊是判斷是否為空,也可以改為是否為0:if mat[u,i]>0:
pui = float(numpy.dot(user_feature[u,:], item_feature[i,:].T))
eui = mat[u,i] - pui
rmse += pow(eui, 2)
n += 1
for k in range(feature):
#Rsvd的更新疊代公式
user_feature[u,k] += gama*(eui*item_feature[i,k] - lamda*user_feature[u,k])
item_feature[i,k] += gama*(eui*user_feature[u,k] - lamda*item_feature[i,k])
#n次疊代平均誤差程度
nowRmse = sqrt(rmse * 1.0 / n)
print 'step: %d Rmse: %s' % ((step+1), nowRmse)
if (nowRmse > preRmse):
pass
else:
break
#降低疊代的步長
gama *= slowRate
step += 1
return user_feature, item_feature 複制
直接調用的結果如下:
step: 1956 Rmse: 0.782449675844
step: 1957 Rmse: 0.782449675843
step: 1958 Rmse: 0.782449675843
step: 1959 Rmse: 0.782449675843
step: 1960 Rmse: 0.782449675842
step: 1961 Rmse: 0.782449675842
step: 1962 Rmse: 0.782449675842
step: 1963 Rmse: 0.782449675841
step: 1964 Rmse: 0.782449675841
step: 1965 Rmse: 0.78244967584
step: 1966 Rmse: 0.78244967584
step: 1967 Rmse: 0.78244967584
step: 1968 Rmse: 0.782449675839
step: 1969 Rmse: 0.782449675839
step: 1970 Rmse: 0.782449675839
step: 1971 Rmse: 0.782449675838
step: 1972 Rmse: 0.782449675838
step: 1973 Rmse: 0.782449675838
step: 1974 Rmse: 0.782449675837
step: 1975 Rmse: 0.782449675837
step: 1976 Rmse: 0.782449675837
step: 1977 Rmse: 0.782449675836
step: 1978 Rmse: 0.782449675836
step: 1979 Rmse: 0.782449675836
step: 1980 Rmse: 0.782449675835
step: 1981 Rmse: 0.782449675835
step: 1982 Rmse: 0.782449675835
step: 1983 Rmse: 0.782449675835
step: 1984 Rmse: 0.782449675834
step: 1985 Rmse: 0.782449675834
step: 1986 Rmse: 0.782449675834
step: 1987 Rmse: 0.782449675833
step: 1988 Rmse: 0.782449675833
step: 1989 Rmse: 0.782449675833
step: 1990 Rmse: 0.782449675833
step: 1991 Rmse: 0.782449675832
step: 1992 Rmse: 0.782449675832
step: 1993 Rmse: 0.782449675832
step: 1994 Rmse: 0.782449675831
step: 1995 Rmse: 0.782449675831
step: 1996 Rmse: 0.782449675831
step: 1997 Rmse: 0.782449675831
step: 1998 Rmse: 0.78244967583
step: 1999 Rmse: 0.78244967583
step: 2000 Rmse: 0.78244967583
Out[15]:
(matrix([[-0.72426432, 0.40007415, 1.16887518],
[-0.73130968, 0.40240702, 1.14708432],
[ 0.34759923, 1.35065656, -0.29573789],
[ 1.17462156, -0.04964694, 0.73881335],
[ 2.04035441, -0.06798676, 1.28078727],
[ 0.30446306, 1.71648612, -0.4109819 ],
[ 1.71963828, -0.00833196, 1.25983483],
[-0.86341514, 0.47750529, 1.36135332],
[-0.48881234, 0.57942923, 0.77110915],
[ 0.29282908, 1.5164249 , -0.39811768],
[ 0.35369432, -0.00964055, 0.22328158]]),
matrix([[ 1.3381854 , -0.05425608, 0.87036818],
[ 1.07547853, -0.04515239, 0.69607952],
[ 1.39038494, -0.05799558, 0.90186332],
[-0.60218508, 0.36233309, 0.92136536],
[ 0.39117217, 1.9272062 , -0.50710187],
[-0.93202395, 0.52982297, 1.43309143],
[-0.19393338, 0.40429152, 0.29994372],
[ 1.40108031, 0.06915628, 0.87647945],
[ 1.39446638, -0.05197355, 0.920216 ],
[ 0.31981929, 1.84114505, -0.40108819],
[-0.82317832, 0.52798144, 1.51619052]])) 複制
svd在推薦算法中的使用
資料集中行代表使用者user,列代表物品item,其中的值代表使用者對物品的打分。
基于SVD的優勢在于:使用者的評分資料是稀疏矩陣,可以用SVD将原始資料映射到低維空間中,然後計算物品item之間的相似度,更加高效快速。
整體思路:
使用者未知得分的商品評分計算方式:
1.使用者的評分矩陣==》使用者已經評分過得商品的得分
2.商品的使用者評分==》使用者已經評分過得商品和其他每個商品的相關性
3.“使用者已經評分過得商品的得分”*“使用者已經評分過得商品和某個未知評分商品的相關系數”=某個未知商品該使用者的評分
計算上面三個步驟,我們需要:
1.考慮采取上面相關性的計算方式
2.考慮潛在因子的個數
依舊python代碼,我會在代碼中注釋講解:
1.首先相關性
# 歐拉距離相似度,評分可用,程度不建議
def oulasim(A, B):
distince = la.norm(A - B) # 第二範式:平方的和後求根号
similarity = 1 / (1 + distince)
return similarity
# 餘弦相似度,評分、1/0、程度都可以用
def cossim(A, B):
ABDOT = float(dot(A, B))
ABlen = la.norm(A) * la.norm(B)
if ABlen == 0:
similarity = '異常'
else:
similarity = ABDOT / float(ABlen)
return similarity
# 皮爾遜相關系數
def pearsonsim(A, B):
A = A - mean(A)
B = B - mean(B)
ABDOT = float(dot(A, B))
ABlen = la.norm(A) * la.norm(B)
if ABlen == 0:
similarity = '異常'
else:
similarity = ABDOT / float(ABlen)
return similarity 複制
2.指定使用者及對應商品的相似度
# svd
def recommender(datamat,user,index,function):
n = shape(datamat)[1] # 商品數目
U, sigma, VT = la.svd(datamat)
# 規約最小維數
sigma2 = sigma ** 2
k = len(sigma2)
n_sum2 = sum(sigma2)
nsum = 0
max_sigma_index = 0
#奇異值的平方占比總數的90%,确定潛在因子數
for i in sigma:
nsum = nsum + i ** 2
max_sigma_index = max_sigma_index + 1
if nsum >= n_sum2 * 0.9:
break
# item new matrix
item = datamat.T * U[:, 0:max_sigma_index] * matrix(diag(sigma[0:max_sigma_index])).I
key=item[index,:]
total_similarity=0
rank_similarity=0
for i in range(k):
#如果使用者沒有評分或者與使用者選擇想知道的商品一緻則跳過,不跳過計算出來前者是得分0,後者直接是使用者已評分的結果,沒有意義
if datamat[user,i]==0 or i==index:continue
similarity=function(key,item[i,:].T)
total_similarity=total_similarity+similarity
#使用者的評分*相關系數
rank_similarity=rank_similarity+similarity*datamat[user,i]*similarity
score = rank_similarity/total_similarity
return score 複制
比如:使用者1在商品1的得分為3.99分
In [18]: recommender(data,1,1,cossim)
Out[18]: 3.98921610058786 複制
3.指定商品,與所有其它商品的相似度
def recommender(datamat, item_set, method):
col = shape(datamat)[1] # 物品數量
item = datamat[:, item_set]
similarity_matrix = zeros([col, 1])
for i in range(col):
index = nonzero(logical_and(item > 0, datamat[:, i] > 0))[0]
if sum(index) > 0:
similarity = method(datamat[index, item_set].T, datamat[index, i])
else:
similarity = '-1'
similarity_matrix[i] = similarity
return similarity_matrix 複制
比如:商品0,對其它所有商品的相似度:
In [24]: recommender(data,0,cossim)
Out[24]:
array([[ 1. ],
[ 0.99439606],
[ 0.99278096],
[-1. ],
[-1. ],
[-1. ],
[-1. ],
[ 0.98183139],
[ 0.97448865],
[-1. ],
[ 1. ]]) 複制
4.直接算出所有商品間的相似度:
def similarity(datamat, method):
item_sum = shape(datamat)[1]
similarity = pd.DataFrame([])
for i in range(item_sum):
res = recommender(datamat, i, method)
similarity = pd.concat([similarity, pd.DataFrame(res)], axis=1)
return similarity 複制
比如商品的相似矩陣:
In [25]: similarity(data,cossim)
Out[25]:
0 0 0 0 0 0 0 \
0 1.000000 0.994396 0.992781 -1.000000 -1.000000 -1.000000 -1.000000
1 0.994396 1.000000 0.999484 -1.000000 -1.000000 -1.000000 -1.000000
2 0.992781 0.999484 1.000000 -1.000000 -1.000000 -1.000000 -1.000000
3 -1.000000 -1.000000 -1.000000 1.000000 -1.000000 0.990375 1.000000
4 -1.000000 -1.000000 -1.000000 -1.000000 1.000000 -1.000000 1.000000
5 -1.000000 -1.000000 -1.000000 0.990375 -1.000000 1.000000 1.000000
6 -1.000000 -1.000000 -1.000000 1.000000 1.000000 1.000000 1.000000
7 0.981831 0.956858 0.955304 -1.000000 1.000000 -1.000000 -1.000000
8 0.974489 0.956858 0.955304 -1.000000 -1.000000 -1.000000 -1.000000
9 -1.000000 -1.000000 -1.000000 1.000000 0.994536 1.000000 0.384615
10 1.000000 1.000000 1.000000 1.000000 -1.000000 0.981307 1.000000
0 0 0 0
0 0.981831 0.974489 -1.000000 1.000000
1 0.956858 0.956858 -1.000000 1.000000
2 0.955304 0.955304 -1.000000 1.000000
3 -1.000000 -1.000000 1.000000 1.000000
4 1.000000 -1.000000 0.994536 -1.000000
5 -1.000000 -1.000000 1.000000 0.981307
6 -1.000000 -1.000000 0.384615 1.000000
7 1.000000 0.991500 1.000000 1.000000
8 0.991500 1.000000 -1.000000 1.000000
9 1.000000 -1.000000 1.000000 1.000000
10 1.000000 1.000000 1.000000 1.000000 複制
5.指定使用者下的top5商品推薦
def fianl_recommender(datamat,user,function):
unratedItems=nonzero(datamat[user,:].A==0)[1]
if len(unratedItems)==0: print 'ok'
score=[]
for i in unratedItems:
i_score=recommender(datamat,user,i,function)
score.append((i,i_score))
score=sorted(score,key=lambda x:x[1],reverse=True)
return score[:5] 複制
比如指定使用者1,最适合推薦的商品如下:
In [31]: fianl_recommender(data,1,pearsonsim)
Out[31]:
[(7, 3.3356853252871588),
(8, 3.3349455396520296),
(0, 3.33492840157654),
(2, 3.334920725716121),
(1, 3.334919898261294)] 複制
最後,謝謝大家閱讀。