WGS84GPS坐标與大地坐标系互相轉化

大地坐标表示順序為：緯度B、經度L、海拔H

空間直角坐标表示方法：X、Y、Z

進行地圖投影等價于将BLH轉換為XYZ，涉及到兩個橢球體以及坐标系之間的轉換，本文主要讨論WGS84坐标系下BLH與XYZ互相轉換的辦法。

WGS84坐标系的參數：

已知長半軸a=6378137 ，

WGS84橢球扁率：f=1/298.257223563

橢球扁率f=（a-b）/a ,可求出b，

橢球第一偏心率：ee=（aa-bb）/aa，帶入可求得e

W為第一輔助系數：W=√(1-e²sin²B) B為緯度

N為橢圓曲率半徑：N=a/W

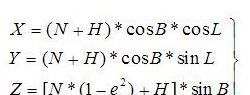
用python代碼寫出：

import math
def get_coordinate(latitude,longitude,altitude):
	B=math.radians(latitude);
	L=math.radians(longitude);
	H=altitude;
	f=1/298.257223563;
	r=6378137;
	b=r*(1-f);
	e=math.sqrt(2*f-f*f);
	N=r/math.sqrt(1-e*e*math.sin(B)*math.sin(B));
	data =[(N+H)*math.cos(B)*math.cos(L),(N+H)*math.cos(B)*math.sin(L),(N*(1-e*e)+H)*math.sin(B)];
	return data;
           

java語言寫成了一個方法：

public static double[] get_coordinate(double latitude,double longitude,double altitude){
		double B=Math.toRadians(latitude) ,L=Math.toRadians(longitude) ,H=altitude,x,y,z;
		double f=1/298.257223563,r=6378137;
		double b=r*(1-f),e=Math.sqrt(2*f-f*f);
		double N=r/Math.sqrt(1-e*e*Math.sin(B)*Math.sin(B));
		x=(N+H)*Math.cos(B)*Math.cos(L);
		y=(N+H)*Math.cos(B)*Math.sin(L);
		z=(N*(1-e*e)+H)*Math.sin(B);
		double[] data ={x,y,z};
		return data;
	}
           

這裡完成了WGS84坐标系轉大地坐标系，但是大地坐标系反解WGS84坐标系較為複雜

我們可以直接通過XY求出L經度，但是對于緯度和海拔求解較為複雜。

這裡我們可以通過一種簡單的方法将計算最簡化。我們将N視為不變，來計算前後GPS坐标。程式如下：

python:

def return_gps(m,n,q):
	f=1/298.257223563;a=6378137;
	b=a*(1-f);e=math.sqrt(2*f-f*f);
	L=math.atan(n/m)+math.pi;
	B=math.atan(math.cos(L)*q/m/(1-N*e*e/(N+40.0038)));
	H=(m/math.cos(L)/math.cos(B)-N+n/math.sin(L)/math.cos(B)-N)/2;
	L1=L/math.pi*180;B1=B/math.pi*180;
	data = [B1,L1,H];
	return data;
           

Java：

public static double[] returnlocation(double m,double n,double q){
		double f=1/298.257223563,a=6378137;
		double b=a*(1-f),e=Math.sqrt(2*f-f*f);
		double L=Math.atan(n/m)+Math.PI;
		double B=Math.atan(Math.cos(L)*q/m/(1-N*e*e/(N+40.0038)));
		double H=(m/Math.cos(L)/Math.cos(B)-N+n/Math.sin(L)/Math.cos(B)N)/2;
		double L1=L/Math.PI*180,B1=B/Math.PI*180;
		double[] data = {B1,L1,H};
		return data;
	}
           

能極大的簡化計算。