Dijkstra（迪傑斯特拉）算法的 java 實作

迪傑斯特拉算法解決的問題是：

在一個有向圖中，求圖中一個節點到其他所有節點的最短距離

算法思路：

每次選取一個離出發點最近且未标記的節點，調整出發點到以這個節點為中心的周邊節點的最短距離。這個過程持續 n - 1 次，直到所有節點都周遊完畢。

假設有一個這樣的圖（圖檔出處：Dijkstra算法Java實作）：

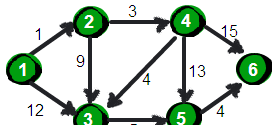
求節點 1 到其他節點的最短距離，代碼實作如下：

public class Test {
    public static void main(String[] args) {
        int MAX = Integer.MAX_VALUE;    // 無法到達時距離設為 Integer.MAX_VALUE
        int[][] weight={
                {0,1,12,MAX,MAX,MAX},
                {MAX,0,9,3,MAX,MAX},
                {MAX,MAX,0,MAX,5,MAX},
                {MAX,MAX,4,0,13,15},
                {MAX,MAX,MAX,MAX,0,4},
                {MAX,MAX,MAX,MAX,MAX,0}
        };
        int start = 0;  // 選擇出發點
        System.out.println(Arrays.toString(solution(weight,start)));
    }

    private static int[] solution(int[][] weight, int start) {
        boolean[] visit = new boolean[weight.length]; // 标記某節點是否被通路過
        int[] res = new int[weight.length];     // 記錄 start 點到各點的最短路徑長度
        for (int i = 0; i < res.length; i++) {
            res[i] = weight[start][i];
        }

        // 查找 n - 1 次（n 為節點個數），每次确定一個節點
        for(int i = 1; i < weight.length; i++) {
            int min = Integer.MAX_VALUE;
            int p = 0;
            // 找出一個未标記的離出發點最近的節點
            for(int j = 0; j < weight.length; j++){
                if(j != start && !visit[j] && res[j] < min){
                    min = res[j];
                    p = j;
                }
            }
            // 标記該節點為已經通路過
            visit[p] = true;

            for (int j = 0; j < weight.length; j++){
                if (j == p || weight[p][j] == Integer.MAX_VALUE) {  // p 點不能到達 j
                    continue;
                }
                if (res[p] + weight[p][j] < res[j]){
                    res[j] = res[p] + weight[p][j];  //更新最短路徑
                }
            }
        }

        return res;
    }
}
           

參考

• Dijkstra算法Java實作