機器學習方法之範數規則
範數規則 實則就是将模型的一些先驗知識融入到模型的學習中,強行地讓學習到的模型具有某些特征,如低秩、稀疏等等,是以可用于防止過拟合現象的出現。
從貝葉斯的角度來看,範數規則項實則對應模型的先驗機率;另外,也可看成是結構風險最小化政策的實作,即在經驗風險上加一個正則化項或者是懲罰項。
一般來說,監督學習即是最小化下面的目标函數:
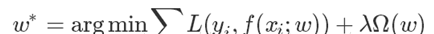
其中,第一項衡量模型(分類/回歸)對第i個樣本的預測值 f ( x i ; ω ) f(x_i;\omega) f(xi;ω) 和真實的值 y i y_i yi 之間的誤差,最小化誤差(第一項)進而保證我們的模型是在拟合訓練樣本;第二項則是對參數 ω \omega ω 的限制,防止過拟合。
L0範數和L1範數
L0範數是指向量中非0元素的個數,将L0範數作為正則項實則是希望向量中的非0元素個數減少,即變得更為稀疏。但是,L0範數由于在0處不可微,難以優化求解(NP-Hard問題),是以常被L1範數代替。
L1範數是指向量中各個元素的絕對值之和,是L0範數的最優凸近似,更容易優化求解,如下圖所示:
L2範數
L2範數是取向量元素的平方和後再開方,也稱"weight decay",可以起到預防過拟合的作用(權值衰減,網絡更簡單)。此外,也有助于處理 condition number 較大情況下的矩陣求逆問題。
(這裡對于第二點好處就不展開論述了,詳見機器學習中的範數規則化之(一)L0、L1與L2範數),但是作為總結簡單說下。首先凸優化中主要有兩大較為棘手問題——局部最小值和 ill-condition 病态問題。ill-condition對應的是well-condition。那他們分别代表什麼?假設我們有個方程組AX=b,我們需要求解X。如果A或者b稍微的改變,會使得X的解發生很大的改變,那麼這個方程組系統就是ill-condition的,對系統輸入的微小變化也很敏感,反之就是well-condition的。condition number衡量的是輸入發生微小變化的時候,輸出會發生多大的變化。也就是系統對微小變化的敏感度。condition number值小的就是well-conditioned的,大的就是ill-conditioned的。)
下面說下L1和L2的差别,為什麼一個讓絕對值最小,一個讓平方最小,會有那麼大的差别呢?
下降規則
L1就是按絕對值函數的“坡”下降的,而L2是按二次函數的“坡”下降。是以實際上在0附近,L1的下降速度比L2的下降速度要快。是以會非常快得降到0。
模型空間的限制
可以看到,L1和每個坐标軸相交的地方都有“角”出現,除了角之外很多邊的輪廓也是有很大的機率成為第一次相交的地方,這都會産生稀疏性。而對于L2-ball,第一次相交的地方出現在具有稀疏性的位置的機率就非常小了,是以不能産生稀疏性。
L1會趨于産生少量的特征,而其他特征都是0,但是L2會選擇更多特征,這些特征都會接近0。
核範數
在介紹核範數之前首先說下矩陣的秩,其實體意義主要是用于衡量矩陣行列之間的相關性。如果矩陣的各行或各列都是線性無關的,則矩陣式滿秩的;如果矩陣各行之間的相關性很強,那麼該矩陣實則可以投影到更低維的線性子空間中,表示成一個低秩的矩陣。
然而,對矩陣求秩rank()是非凸的,難以優化求解,是以就需要尋求它的凸近似,即為核範數 ∣ ∣ ω ∣ ∣ ∗ ||\omega||_* ∣∣ω∣∣∗。
首先給出數學公式,摘自淺說範數規範化(二)—— 核範數:
可以看出核範數實則表示奇異值/特征值的和,rank()表示的是非零奇異值的個數,是以可以了解為L1與L0範數之間的關系。
核範數的應用之一:魯棒PCA(RPCA)
RPCA的基本思想是将原矩陣分解為兩個矩陣相加,一個是低秩矩陣(原矩陣含有一定的結構資訊,是以各行/各列是線性相關的),另一個是稀疏的(原矩陣中含有噪聲,噪聲是稀疏的),是以目标函數可以寫成:
與經典PCA相同的是,RPCA本質上也是尋找資料在低維空間上的最佳投影問題。對于低秩資料觀測矩陣X,假如X受到随機(稀疏)噪聲的影響,則X的低秩性就會破壞,使X變成滿秩的。是以我們就需要将X分解成包含其真實結構的低秩矩陣和稀疏噪聲矩陣之和。找到了低秩矩陣,實際上就找到了資料的本質低維空間。
與經典PCA問題不同的是,因為PCA假設我們的資料的噪聲是高斯的,對于大的噪聲或者嚴重的離群點,PCA會被它影響,導緻無法正常工作。而RPCA則不存在這個假設。它隻是假設它的噪聲是稀疏的,而不管噪聲的強弱如何。
為便于優化求解,通常将原問題松弛到凸優化問題:
語音方面應用
有一類語音增強方法是基于RPCA模型的語音增強方法,認為帶噪語音信号可以分解為低秩的噪聲和稀疏的語音信号(語音信号往往隻在若幹個頻點表現活躍),但是實驗結果表明獲得的系數矩陣中殘留較多的噪聲,低秩矩陣中也含有較多的語音資訊,并不能實作很好的分離效果。因為語音時頻譜矩陣除了具有稀疏性以外,也具有一定的低秩特性。
此外,在參考文獻[3]中作者是将帶噪語音分為低秩 L,稀疏 S和噪聲 N三部分,其中低秩部分代表結構化噪聲(結構化噪聲部分通常具有比語音信号更加明顯的重複和備援結構),稀疏部分代表語音,而噪聲則代表是非結構化噪聲,這部分的分解運算可由GoDec算法實作。然而,由于單純的稀疏低秩分解得到的低秩部分更關注信号在時頻域的重複性而不側重于研究這些重複信号所具有的具體特征,為此文獻[3]提出對L用非負矩陣分解以學習到結構化噪聲字典,具體如下:
其他改進算法我也沒有多看,便不多說了。
參考博文:
原文1:https://blog.csdn.net/zouxy09/article/details/24972869
原文2:http://sakigami-yang.me/2017/09/09/norm-regularization-02/
[3] : 稀疏低秩模型下的單通道自學習語音增強算法