新的一周又開始了,作為引子的review,還是有點長的,大家可以耐心的讀讀,絕對會讓你有種豁然開朗的感覺。下周的重點是統計語言模型,别想的那麼複雜,實際上就是貝葉斯機率和線性代數。竊以為,所謂以代碼來講解算法的,就是在教育訓練碼農,而不是一名合格的程式員。雖然,作為應用的學科,證明并不是那麼像純數學那樣重要,但總歸還是得明白原理吧。
ps1:新一季的《黑鏡》還是那麼的讓人看完後,流下陣陣冷汗。
ps2:下周要好好弄下排版了,這兩天晚上都是玩遊戲去了,懶。
5.多面性的過拟合
如果我們所擁有的知識和資料不足以完全确定正确的分類器,怎麼辦?那我們運作的隻是幻覺的一個分類器(或其中的一部分)的風險,卻不是基于現實的基礎,并且隻是在資料中奇怪的編碼随機。這個問題被稱為過拟合,是機器學習的bug。當你的學習者輸出一個對訓練資料100%準确的分類器,但是對測試資料隻有50%的精确度時,事實上它可以輸出一個對兩者都75%精确的分類器,就已經過拟合了。
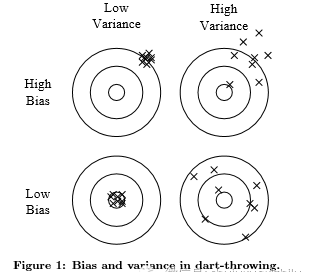
機器學習領域的每個人都知道過拟合,但它有許多形式,并不那麼顯而易見。了解過拟合的一種方法是将廣義誤差分解為偏差和方差。偏差是學習者總是具有學習同樣錯誤的東西的傾向。方差是學習随機事物的趨勢,而不考慮真實信号。圖1通過在闆上投擲飛镖的類比來說明這一點。線性學習者具有高偏差,因為當兩個類之間的邊界不是超平面時,學習者不能歸納它。決策樹沒有這個問題,因為他們可以表示任何布爾函數,但另一方面,他們可以從高方差:在不同訓練集中的相同現象學習再泛化的決策樹通常是不同的,事實上,他們應該是相同的。類似的推理适用于優化方法的選擇上:束搜尋具有比貪婪搜尋更低的偏差,但更高的方差,因為它嘗試更多的假設。是以,與直覺相反,更強大的學習者不一定比不那麼強大的學習者更好。
圖2說明了這一點。即使真正的分類器是一組規則,最多1000個例子樸素貝葉斯比規則學習者更準确。這依然發生了,盡管樸素貝葉斯的假設前沿是線性的!這樣的情況在機器學習中是常見的:強假假設可能優于弱假假設,因為學習者需要更多的資料來避免過拟合。
交叉驗證可以幫助對抗過拟合,例如通過使用它來選擇最佳尺寸的決策樹來學習。但它不是靈丹妙藥,因為如果我們使用它做出太多的參數選擇,它本身可以開始過拟合了。
除了交叉驗證,還有許多方法來對抗過度。最流行的一種是向評估函數添加正則化項。例如,這可以懲罰有着更複雜結構的分類器,進而是的較小的分類器隻有較少的空間去過拟合。另一個選擇是在添加新結構之前執行像卡方檢驗那樣的統計學意義檢驗,以确定類的分布是否是不同的并且具有/不具有這種結構。當資料非常稀缺時,這些技術特别有用。然而,你應該懷疑有一種特定技術可“解決”過拟合的說。避免了過拟合(方差),卻很容易落入了相反的誤差,欠拟合(偏差)。同時避免兩者都需要學習一個完美的分類器,在缺乏知識的情況下,沒有唯一的技術可以永遠做的最好(沒有免費的午餐)。
關于過拟合的一個常見誤解是,它是由噪聲引起的,例如标記有錯誤類的訓練樣本。這确實可以加深過拟合,通過使學習者畫一個反複無常的邊界,以保持這些它自認為是正确的樣本。但是即使在沒有噪聲的情況下也可能發生嚴重的過拟合。例如,假設我們學習一個布爾分類器,它隻是訓練集中标記為“真”的示例的分離。(換句話說,分類器是一個析取範式的布爾公式,其中每個項是一個特定訓練樣本的特征值的連接配接)。這個分類器得到所有的正确的訓練樣本和所有錯誤的積極的測試樣本,而不考慮訓練資料是否有噪聲。
多重測試的問題與過拟合密切相關。标準統計檢驗假設隻有一個假設正在測試,但現代學習者可以在他們完成之前輕松測試數百萬資料。是以,看起來有意義的實際上可能沒有意義。例如,一個連續十年打破市場的共同基金看起來非常令人印象深刻,直到你意識到,如果有1000個基金,每個基金在任何一年有50%的機會擊敗市場,很可能有一個将成功十次,這隻是運氣而已。這個問題可以通過糾正顯著性檢驗來去考慮相當數量的假設來解決,但這可能導緻欠拟合。更好的方法是控制錯誤接受的非零假設的分數,這稱之為假發現率。
6.高次元下的直覺喪失
過拟合之後,機器學習中最大的問題是次元的詛咒。這個表達是由貝爾曼在1961年提出的,指的是當輸入是高維時,許多在低維中工作的算法會變得棘手。但在機器學習中它指的是更多。 由于固定大小的訓練集會導緻輸入空間逐漸減少覆寫,是以随着樣本次元(特征數目)的增加,正确地泛化成指數地的難度增加。即使中等的次元為100的訓練集和巨大的具有一萬億個樣本的訓練集,後者僅覆寫輸入空間的大約10-18的部分。這就是為什麼會使得機器學習既必要又困難。
更嚴重的是,機器學習算法共性的毛病是依賴(基于顯式或隐式)在高次元上的分解。考慮hamming距離的k近鄰分類器作為相似性度量,并假設該類隻是x1∧x2。 如果沒有其他特征,這是一個簡單的問題。但是如果存在98個不相關的特征x3,...,x100,則來自它們的噪聲完全可以在x1和x2中的信号進行求和,并且距離最近的樣本可以有效地進行随機預測。
更令人不安的是,即使所有100個特征都相關,距離最近的樣本仍然有問題!這是因為在高次元中,所有樣本都相似。 例如,假設樣本布局在規則網格上,并考慮測試樣本xt。如果網格是d維的,xt的2D最近的樣本都離它具有相同的距離。是以,随着維數的增加,越來越多的樣本成為xt的最近鄰,直到最近鄰(以及類的)的選擇是有效随機。
這隻是高次元下一個更一般問題的一個執行個體:我們來自三維世界的直覺,通常不适用于高次元。在高次元中,多元高斯分布的大部分權重不是接近平均值,而是在它周圍越來越遠的“殼”; 并且大部分的高次元的橙色是在皮膚,而不是紙漿。如果恒定數量的樣本均勻分布在高維超立方體中,再比他高一些的次元裡大多數樣本比它們最近鄰更靠近超立方體的面。如果我們通過在超立方體中寫入超球面來近似超球面,在高次元中,超立方體的幾乎所有體積都在超球面之外。這是機器學習的壞消息,其中一種類型的形狀通常由另一種的形狀近似。
在二維或三維上建構分類器很容易; 我們可以通過可視化發現在不同類别的樣本之間找到合理的邊界。(甚至有人說,如果人們可以看到高次元,機器學習是沒有必要的。)但在高次元很難了解發生了什麼。這反過來使得設計一個好的分類器變得困難。原來,人們可能認為收集更多的特征從來就不會有事,因為在最壞的情況下,他們也不提供關于類的新資訊。但事實上,他們的優點可能超過次元的詛咒。
幸運的是,有一個效應部分地抵消掉了詛咒,這可以被稱為“非均勻性的祝福”。在大多數應用中,樣本不是均勻地遍布整個執行個體空間,而是集中在較低次元的多面體上或其附近。例如,即使數字的圖像每個像素具有一個次元,k-最近鄰也能很好地用于手寫數字識别,因為數字圖像的空間比所有可能的圖像的空間小得多。學習者可以隐含地利用這個較低的效率次元,或者可以使用用于顯式地減少次元的算法
7.并非想像中的次元
機器學習論文充滿了理論保證。最常見的類型是確定良好泛化所需的樣本數量的界限。 你應該怎麼做這些保證?首先,它是令人驚訝的,甚至他們存在可能。歸納在傳統上與推理形成對照:在推理過程中,您可以保證結論是正确的; 在歸納中,所有賭注是關閉的。或許是幾個世紀的傳統智慧。 近幾十年的主要發展之一是認識到,事實上,我們可以對歸納的結果有保證,特别是如果我們能夠解決機率保證。
基本的論點非常簡單。假設如果分類器的真實錯誤率大于ǫ,則它是壞的。然後,壞的分類器與n個随機,獨立訓練樣本一緻的機率小于(1-ǫ)n。令b是學習者假設空間H中的壞分類器的數量。通過聯合界知至少其中一個一緻機率小于b(1-ǫ)n。假設學習者總是傳回一緻的分類器,則該分類器是壞的機率小于|H|(1-ǫ)n,其中我們使用b|H|的事實。 是以,如果我們希望這個機率小于δ,它使得n> ln()/ ln(1-ǫ)(ln|H|+ln)。
不幸的是,這種類型的保證必須有保留的。這是因為以這種方式獲得的邊界通常非常寬松。上述限制精彩的特征是所需數量的樣本僅與|H|對數增長和1 /δ。不幸的是,最有趣的假設空間是特征數量d階的雙指數函數,這仍然使我們需要相當樣本數量的d階指數。例如,考慮d個布爾變量的布爾函數的空間。如果擁有e個可能不同的樣本,就會有2e個可能不同的函數,是以有2d可能函數,總函數數為。即使對于“隻是”指數的假設空間,界限仍然非常松散,因為聯合界是非常悲觀的。例如,如果有100個布爾特征,并且假設空間是具有多達10個水準的決策樹,我們需要50萬個樣本去保證在上述限制中δ= ǫ = 1%。但在實踐中,隻有其中的小部分用于精确學習。
此外,我們必須小心思考邊界是什麼意思。 例如,并不是說,如果你的學習者傳回一個符合特定訓練集的假設,那麼這個假設可能泛化得很好。準确而言是給定一個足夠大的訓練集,很可能你的學習者将傳回一個泛化的很好或不能找到一個一緻的假設的假設。邊界也沒有提供如何選擇一個好的假設空間。它隻告訴我們,如果假設空間包含真正的分類器,那麼學習者輸出不好的分類器的機率随訓練集大小而減小。如果我們減少假設空間,改善邊界,那麼它包含真正的分類器的機會也縮小。(對于真實分類器的邊界存在不在假設空間的情況,但是類似的考慮同樣适用于它們。)
另一種常見類型的理論保證是漸近:在有限資料集中,學習者保證輸出正确的分類器。 這是令人放心的,但由于其漸近的保證,選擇一個學習者而不是另一個學習者會是輕率的選擇。在實踐中,我們很少使用漸近機制(也稱為“漸近”)。并且,由于我們上面讨論的偏差 - 方差平衡,如果在給定的有限資料集中學習者A比給出的學習者B更好,B通常比A在給定的無限資料集中更好。
理論保證在機器學習中的主要作用不是作為實際決策的标準,而是作為算法設計的了解來源和驅動力。在這方面,他們是非常有用的; 确實,理論與實踐的密切互相作用是機器學習多年來取得如此巨大進步的主要原因之一。 但是需要注意的是:學習是一個複雜的現象,僅僅因為學習者同時擁有理論上的支撐和實踐中的可運作,而不是意味着前者是後者的原因。
8.關鍵在于特征工程
在一天結束時,一些機器學習項目成功了,一些失敗了。是什麼造成了這些差異? 簡單的來講,最重要的因素是使用的特征。 如果你有許多獨立的功能,每個都與類很好地相關,學習很容易。另一方面,如果類是一個非常複雜的特征的函數,你可能無法學習它。 通常,原始資料不是以适合學習的形式,但是你可以從它構造特征。 這通常占據機器學習項目中的大部分時間,通常也是最有趣的部分之一,其中直覺,創造力和“黑色藝術”與技術stuff一樣重要。
初學者通常對機器學習項目花費在機器學習上時間之少感到驚訝。 但是,如果您考慮收集資料,整合資料,清理資料和對資料進行預處理以及在特征設計中可以進行多少試驗和錯誤,這是很有意義的。此外,機器學習不是建構資料集和運作學習者的一次性過程,而是運作學習者,分析結果,修改資料和/或學習者并重複的疊代過程。學習通常是這方面最快的部分,但這是因為我們已經掌握的很好了! 特征工程更加困難,因為它是特定領域,而學習者可以在很大程度上是通用的。 然而,兩者之間沒有分明的邊界,這是最有用的學習者是能輕易結合知識的另一個原因。
當然,機器學習的一個聖杯是自動化越來越多的特征工程的處理過程。 這種方法今天經常進行的一種方式是自動生成大量的候選特征,并通過相對于類的(例如)資訊增益來選擇最佳。但請記住,在單獨空間中看起來無關的特征可能是相關的。 例如,如果類是k個輸入特征的XOR,則它們中的每一個本身不攜帶關于類的資訊。 (如果你想惹惱機器學習者,提出XOR。)另一方面,運作一個攜帶大量特征的學習者,以找出哪些是有用的組合可能太費時,或導緻過拟合。是以,沒有一種最終沒有可替代性的智能讓你節省掉特征工程。
9.更多的資料打敗了更聰明的算法
假設你已經建構了最好的特征集,但是你得到的分類器仍然不夠準确。你現在能做什麼? 有兩個主要的選擇:設計一個更好的學習算法,或收集更多的資料(更多的樣本,可能更多的原始特征,臣服于受到次元的詛咒)。機器學習研究者主要關注前者,但實際上,最快的成功之路往往是獲得更多的資料。 作為一個經驗法則,具有大量的啞算法和大量資料可以擊敗一個更聰明的算法。(畢竟,機器學習是關于讓資料做主要工作的。)
但是這又帶來了另一個問題:可擴充性。在大多數計算機科學中,兩個主要的有限資源是時間和空間。 在機器學習中,有第三個:訓練資料。無論哪一個瓶頸的改變都需要數十年的時間。在20世紀80年代,它往往是資料。今天經常是時間。有大量的資料可用,但沒有足夠的時間來處理它,是以它沒有使用。這也導緻了沖突:即使原則上更多的資料意味着可以學習更複雜的分類器,在實踐中更簡單的分類器被使用,因為複雜的分類器花費太長時間來學習。 答案的一部分是提出快速的方法來學習複雜的分類器,并且在這個方向上已經取得了顯着的進步。
使用更聰明的算法的部分原因可以比你預期的具有更小的回報,對于第一次近似而言,他們做的都一樣的。 這是令人驚訝的,例如當你考慮将表示視為不同的規則集合和神經網絡。但實際上命題規則容易編碼為神經網絡,并且其他表示之間存在類似的關系。 所有學習者基本上通過将附近的樣本分組到同一類中來工作;關鍵差異在于“附近”的含義上。由于非均勻分布的資料,學習者可以産生廣泛而不同的邊界,同時仍然在重要的地區(那些具有大量的訓練樣本,是以也是大多數測試樣本很可能出現的地方)。這也有助于解釋為什麼強大的學習者可能不穩定,但仍然準确。圖3在2-D中展示出了這一點;該效應在高次元上更強。
作為一個規則,首先應該嘗試最簡單的學習者(例如,樸素貝葉斯之前的logistic回歸,k近鄰算法之前的支援向量機)。 更複雜的學習者是誘人的,但他們通常更難使用,因為他們有更多的參數,你需要調整來得到好的結果,并且因為他們的内部更不透明。
學習者可以分為兩種主要類型:表示具有固定大小的那些,如線性分類器,以及其表示可以随資料一起增長的那些,例如決策樹。 (後者有時被稱為非參數學習者,但這是有點不幸,因為他們通常學習的參數比參數的更多)。固定大小的學習者隻能利用這麼多的資料。(注意圖2中樸素貝葉斯漸近的精确度在70%左右。)大小可變的學習者原則上可以學習給定足夠資料的任何函數,但在實踐中他們可能不會,因為算法的限制(例如,貪婪搜尋落入局部最優)或計算成本。此外,由于次元的詛咒,沒有現有的資料量可能是足夠的。因為這些原因,聰明的算法 - 那些能夠充分利用資料和計算資源的算法 - 如果您願意投入足夠多的努力,通常最終會給予你回報。在設計學習者和學習分類器之間沒有尖銳的邊界;相反,任何給定的知識都可以在學習者中編碼或從資料學習。是以,機器學習項目經常在結束時有一個學習者設計的重要組成部分,并且參與者需要有一些專業知識。
最後,最大的瓶頸不是資料或CPU周期,而是人類周期。在研究論文中,學習者通常在準确度和計算成本的度量上進行比較。人類的節省的精力和獲得的洞察,雖然更難以衡量,但往往更重要。這有利于産生人類可了解輸出的學習者(例如規則集)。充分利用機器學習的組織是那些具有基礎設施的組織,這些組織使得許多不同的學習者,資料源和學習問題的實驗變得容易和有效,以及機器學習專家和應用領域之間聯系更加緊密。
10.學習許多模型,而不是一個
在機器學習的早期,每個人都有他們最喜歡的學習者,再摻雜上一些先驗的理由進而相信它的優越性。大多數人都試圖嘗試許多版本,并選擇最好的一個。然後系統的經驗比較表明,最好的學習者随着應用實踐的變化而變化,包含許多不同的學習者的系統開始出現。努力的重心現在是嘗試衆多學習者的許多版本,并仍然選擇最好的一個。但是後來研究人員注意到,如果不是選擇發現的最佳版本,而是我們結合了許多版本,結果更好 - 通常更好 - 并且對使用者隻需要一點額外的努力。
建立這樣的模型集是現在的标準。在最簡單的技術,稱為裝袋(bagging),我們簡單地通過重采樣生成訓練集的随機變化,學習每個分類器,并通過投票(voting)結合結果。 這是因為它大大減少方差,而隻是稍微增加偏差。 在boosting中,訓練樣本具有權重,并且這些權重是不同的,是以每個新的分類器都關注之前的樣本。在stacking中,單個分類器的輸出成為“更進階”學習者的輸入,以确定如何最好地組合它們。
存在許多其他技術,并且趨勢是朝向更大的集合。 在Netflix獎中,來自世界各地的團隊競相制作最好的視訊推薦系統(http:// net fl ixprize.com)。 随着比賽的進行,團隊發現他們通過将學習者與其他團隊結合在一起,獲得了最好的結果,并被合并成了更大的團隊。獲勝者和亞軍都是超過100名學生的堆疊的團隊,并結合兩個團隊進一步改善了結果。 毫無疑問,我們将來會看到更大的。
模型集合不應與貝葉斯模型平均(BMA)混淆。BMA是理論上學習的優化方法。在BMA中,通過對假設空間中所有分類器的個體預測進行平均來對新樣本進行預測,通過分類器解釋訓練資料的程度以及我們相信它們的先驗程度進行權重權重。盡管他們的超級相似,集合和BMA是非常不同的。集合改變假設空間(例如,從單個決策樹到它們的線性組合),并且可以采取各種各樣的形式。 BMA根據固定的公式對原始空間中的假設配置設定權重。 BMA權重與(例如)裝袋(bagging)或增強(boosting)産生的BMA權重非常不同:後者是相當均勻的,而前者是非常不均的,直到單個最高權重分類器經常占據主導地位,使BMA有效等同的選擇它。這樣做的一個實際結果是,盡管模型集合是機器學習工具包的關鍵部分,BMA是很少有有價值的麻煩。
11.簡單而不是精确的
有名的奧卡姆剃刀論述到實體不應該超越必要性。 在機器學習中,這往往意味着,給定兩個具有相同訓練誤差的分類器,兩者中較簡單的可能具有最低的測試誤差。這種說法的證據經常出現在文獻中,但實際上有許多反例,“天下沒有免費午餐”定理意味着它不是真的。
我們在上一節中看到了一個反例:模型集合。 即使在訓練誤差已經達到零之後,通過添加分類器,增強集合的泛化誤差仍然得到了改善。 另一個反例是支援向量機,它可以有效地擁有無限數量的參數,而沒有過拟合。相反,sign(sin(ax))可以區分x軸上任意大的任意标記的點集合,即使它隻有一個參數。 是以,與直覺相反,模型的參數數量及其過拟合傾向之間沒有必要的聯系。
更複雜的視圖代之以與假設空間的相同大小的複雜度,因為較小的空間允許假設由較短的代碼表示。類似上述理論保證部分中的邊界可能被視圖化暗示着較短的假設泛化的更好。這可以通過為我們有一些先驗偏好的空間中的假設配置設定更短的代碼來進一步定義。 但是這可以視為是準确性和簡單性之間的“證明”是循環推理:我們做出了假設,我們更喜歡簡單的設計,如果他們是準确的,這是因為我們的偏好是準确的,而不是因為在我們選擇的表示種假設是“簡單的”。
進一步的複雜性産生于以下事實:少數學習者窮盡地搜尋其假設空間。 具有更大假設空間的學習者嘗試更少的假設,比從更小的空間嘗試更多假設的學習者具有更少的過拟合。正如Pearl指出的,假設空間的大小隻是粗略的指導對于相關的訓練和測試誤差真正重要的是:選擇哪一個假設的步驟。
Domingos調查了關于機器學習中奧卡姆剃刀問題的主要論點和證據。結論是,更簡單的假設應該是優選的,因為簡單性本身就是一種美德,而不是因為與假設連接配接的精确性。這可能是Occam在第一個地方的意思。
13.表示不明确
基本上,可變大國小習器中使用的所有表示都具有“每個函數可以被表示或使用該表示來任意接近近似”形式的相關定理。由此表示的支援的粉絲經常進行忽略所有其他。然而,隻是因為一個函數可以表示并不意味着它可以學習。例如,标準決策樹學習者不能學習具有比訓練樣本更多的樹的枝葉。在連續空間中,表示甚至是使用固定的一組基元的簡單函數通常都需要無限數量的成分。此外,如果假設空間具有評估函數的許多局部最優值,通常情況下,學習者可能不能找到真實函數,即使它是可表示的。給定有限資料,時間和空間,标準學習者隻能學習所有可能函數的一小部分,這些子集對于具有不同表示的學習者是不同的。是以,關鍵問題不是“它能代表嗎?”,這個的答案往往是不值得關心的,但是“可以學習嗎?”它值得不同的學習者去嘗試(可能結合它們)。
對于某些函數,某些表示比其他表示在指數上更緊湊。是以,他們也可能需要呈指數減少的資料來學習這些函數。 許多學習者通過形成簡單基函數的線性組合來工作。例如,支援向量機形成以一些訓練樣本(支援向量)為中心的核心的組合。 以這種方式表示n位的奇偶性需要2n個基函數。 但是使用具有更多層的表示(即在輸入和輸出之間更多的步長),可以線上性大小的分類器中對奇偶性進行編碼。尋找方法來學習這些更深刻的表示是機器學習的主要研究前沿之一。
14.相關性不意味着因果性
相關性并不意味着因果關系的這一點經常發生,以至于它可能不值得一章。 但是,即使我們一直在讨論的那種學習者隻能學習相關性,他們的結果通常被視為代表因果關系。這是不是錯了? 如果是這樣,那麼為什麼人們做呢?
通常,學習預測模型的目的是使用它們作為行動指南。 如果我們發現啤酒和尿布經常在超市一起買,那麼或許把啤酒放在尿布部分旁邊會增加銷售。(這是資料挖掘世界中一個着名的例子。)但是實際上能否做到這個實驗的效果是很難分辨的。機器學習通常應用于觀察資料,其中預測變量不在學習者的控制之下,也不是在實驗資料的地方。一些學習算法可能從觀測資料中提取因果資訊,但它們的适用性相當有限。另一方面,相關性是潛在的因果關系的标志,我們可以使用它作為進一步調查的指南(例如,試圖了解因果鍊可能是什麼)。
許多研究人員認為因果關系隻是一個友善的選擇。 例如,實體法則中沒有因果關系的概念。 是否存在因果關系是一個深刻的哲學問題,沒有明确的答案,但機器學習者的實用點是兩個。首先,無論我們稱之為“因果”,我們都希望預測我們行動的影響,而不僅僅是可觀察變量之間的相關性。 第二,如果你可以獲得實驗資料(例如通過随機配置設定通路者到一個網站的不同版本),那就盡管這樣做。
14.結論
像任何學科一樣,機器學習有很多很難實作的“民間智慧”,但是對成功至關重要。 本文總結了一些最突出的項目。 一個學習好地方是我的書“The Master Algorithm”,一個非技術的機器學習介紹。 有關完整的線上機器學習課程,請通路http://www.cs.washington.edu/homes/pedrod/class。 還有一個機器學習講座的寶庫在http://www.videolectures.net。廣泛使用的開源機器學習工具包是Weka。快樂學習!