一.字首表達式
(一)介紹
字首表達式又稱波蘭式,字首表達式的運算符位于操作數之前。
運算規則:
•對字首表達式進行從右至左依次掃描•當遇到數字時,将數字壓入堆棧,遇到運算符時,彈出棧頂的兩個數,用運算符對它們做相應的計算(棧頂元素 op 次頂元素),并将結果入棧
•重複上述過程直到表達式最左端,最後運算得出的值即為表達式的結果
(二)運算分析
例如:中綴表達式 ( 2 + 3 ) × 4 - 5,采用字首表達式為:- × + 2 3 4 5
思路分析:
•從右至左掃描,将5、4、3、2壓入堆棧•遇到 + 運算符,是以彈出 2 和 3( 2 為棧頂元素,3 為次頂元素,注意與字尾表達式做比較),計算出 2 + 3 的值,得 5,再将 5 入棧;•接下來是 × 運算符,是以彈出 5 和 4 ,計算出 5 × 4 = 20,将 20 入棧•最後是 - 運算符,計算出 20 - 5 的值,即 15,由此得出最終計算結果
中綴表達式轉為字首表達式:
轉換步驟如下:
•(1)初始化兩個棧:運算符棧 s1,儲存中間結果的棧 s2
•(2)從右至左掃描中綴表達式
•(3)遇到操作數時,将其壓入 s2
•(4)遇到運算符時,比較其與 s1 棧頂運算符的優先級
•①:如果 s1 為空,或棧頂運算符為右括号 “ ) ”,則直接将此運算符入棧
•②:否則,若優先級比棧頂運算符的較高或相等,也将運算符壓入 s1
•③:否則,将 s1 棧頂的運算符彈出并壓入到 s2 中,再次轉到 ( 4 - 1 ) 與 s1 中新的棧頂運算符相比
•(5)遇到括号時
•①:如果是右括号“)”,則直接壓入 s1
•②:如果是左括号“(”,則依次彈出 s1 棧頂的運算符,并壓入 s2 ,直到遇到 右括号為止,此時将這一對括号丢棄
(6)重複步驟(2)至(5),直到表達式的最左邊••
(7)将 s1 中剩餘的運算符依次彈出并壓入 s2••
(8)依次彈出 s2 中的元素并輸出,結果即為中綴表達式對應的字首表達式。
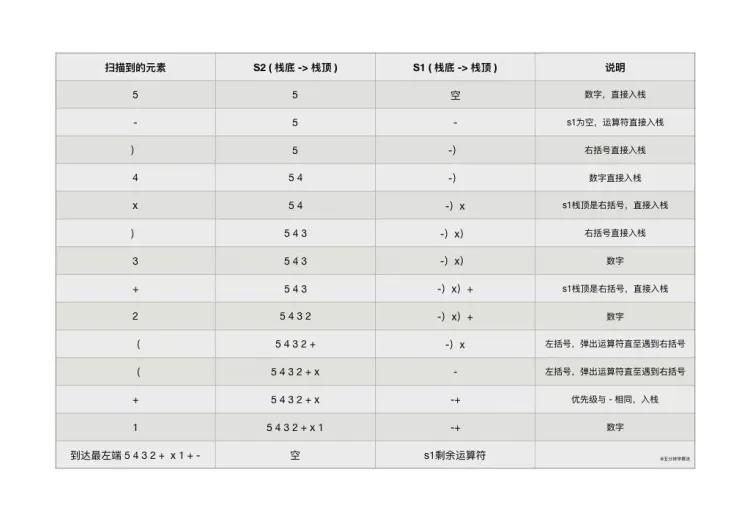
例如:中綴表達式 1 + (( 2 + 3 ) × 4) - 5 轉為字首表達式具體過程,如下圖
(三)具體代碼
package stack;
import javax.xml.transform.stream.StreamSource;
/**
* @author Jin
* @ Date 2022年07月2022/7/1日0:59
* 字首表達式
* 通過棧來實作簡單的運算器(可以進行加減乘除等基本運算)
*/
public class CalculatorStack {
public static void main(String[] args) {
String expression ="3+4*8-20";
ArrayStack2 numStack=new ArrayStack2(10);
//數棧,用來存儲運算數
ArrayStack2 operStack=new ArrayStack2(10);
//符棧,用來存儲運算符
int index=0;
int num1=0;
int num2=0;
int oper=0;
int res=0;
char ch=' ';
String KeepNum="";
//将每次掃描得到的字元儲存到ch
//開始while循環的掃描expression
while(true){
//依次得到expression的每一個字元
ch=expression.substring(index,index+1).charAt(0);
//判斷ch是什麼,然後再進行相應操作
if(operStack.isOper(ch)){
//ch是運算符,判斷目前棧是否為空
if(operStack.isEmpty()){
operStack.push(ch);
}else{
//符号棧不為空
/*比較待插入棧中運算符的優先級<①>和符棧頂的運算符之間的優先級關系<②>
* (1)如果①的優先級小于等于②
* 從數棧中彈出兩個運算數,從符号棧中彈出棧頂運算符②,然後進行運算
* 将運算結果壓入數棧,将符号①壓入符棧
* (2)如果①的優先級大于②
* 将符号①壓入符号棧
* */
if(operStack.priority(ch)<= operStack.priority(operStack.getHead())){
num1=numStack.pop();
num2=numStack.pop();
oper=operStack.pop();
res=operStack.cal(num1,num2,oper);
numStack.push(res);
operStack.push(ch);
//将計算結果和符号分别壓入數棧和符号棧
}else{
operStack.push(ch);
}
}
}else{
/* numStack.push(ch-48); ----> 沒有考慮到多位數 */
/**
* 多位數分析思路:
* (1)當處理多位數時,不能發現是一位數字就入棧
* (2)如果掃描的第一位是數字,再向後掃描一位,若是符号,掃描的第一位就入數字棧
* (3)如果第二位也是數字,使用變量字元串進行拼接,依次如此
* */
//處理多位數
KeepNum += ch;
/*判斷ch是不是最後一個字元*/
if(index==expression.length()-1){
numStack.push(Integer.parseInt(KeepNum));
}else{
//判斷下一個字元是不是數字
if(operStack.isOper(expression.substring(index+1,index+2).charAt(0))){
numStack.push(Integer.parseInt(KeepNum));
KeepNum="";
//注意:一定要将KeepNum置空,否則會出現字元串越界問題
}
}
}
//讓 index+1,然後判斷是否掃描到expression最後
index++;
if(index>=expression.length()){
break;
}
}
//表達式掃描完畢,開始從兩個棧中開始取符号和數字進行運算
while(true){
//符号棧為空,則計算到最後的結果,數棧中隻有一個數字【結果】
if(operStack.isEmpty()){
break;
}else{
num1=numStack.pop();
num2=numStack.pop();
oper=operStack.pop();
res=operStack.cal(num1,num2,oper);
numStack.push(res);
}
}
int last=numStack.pop();
System.out.printf("表達式%s =%d",expression,last);
}
}
/**建立一個棧*/
class ArrayStack2{
private int maxSize;
private int[]stack;
private int top=-1;
/**構造器*/
public ArrayStack2(int maxSize){
this.maxSize=maxSize;
stack=new int[maxSize];
}
/**(1)判斷棧是否滿*/
public boolean isFull(){
return top==maxSize-1;
}
/**(2)判斷棧空*/
public boolean isEmpty(){
return top==-1;
}
/**(3)入棧(将資料壓入棧頂)*/
public void push(int value){
if(isFull()){
System.out.println("棧已經滿,無法進行添加新元素!!");
}else{
top++;
stack[top]=value;
}
}
/**(4)出棧(将棧頂的元素取出)*/
public int pop(){
if(isEmpty()){
throw new RuntimeException("棧空,沒有資料!");
}else{
int middle =stack[top];
top--;
return middle;
}
}
/**(5)周遊棧中元素(從棧頂到棧底開始周遊)*/
public void showStack(){
if(isEmpty()){
System.out.println("棧空,沒有資料~~");
return;
}
for (int i = top; i >=0 ; i--) {
System.out.printf("stack[%d]=%d\n",i,stack[i]);
}
}
/**(6)檢視棧頂元素*/
public int getHead(){
return stack[top];
}
/**傳回運算符的優先級,優先級使用數字表示,數字越大,其優先級就越高*/
public int priority(int oper){
if(oper=='*'||oper=='/'){
return 1;
}else if(oper=='+'||oper=='-'){
return 0;
}else{
return -1;
}
}
/**判斷是不是運算符*/
public boolean isOper(char val){
return val=='*'||val=='/'||val=='+'||val=='-';
}
/**計算方法*/
public int cal(int num1,int nums2,int oper){
int res=0;
//res用于存儲計算的結果
switch(oper){
case'+': res=num1+nums2 ;break;
case'-': res=nums2-num1 ;break;
case'*':res=num1*nums2;break;
case'/':res=nums2/num1;break;
default:break;
}
return res;
}
} 二.字尾表達式
(一)介紹
字尾表達式又稱逆波蘭式,字尾表達式的運算符位于操作數之後。
規則:
從左到右周遊表達式的每個數字和符号,遇到是數字就進棧,遇到是符号,就将處于棧頂兩個數字出棧,進行運算,運算結果進棧,一直到最終獲得結果。
(二)運算分析
(三)具體代碼
package stack;
import java.util.*;
import java.util.Stack;
/**
* @author Jin
* @ Date 2022年07月2022/7/1日13:26
* 功能:
* (1)将中綴表達式轉化為字尾表達式
* (2)求解字尾表達式
*/
public class PolandNotation {
public static void main(String[] args) {
/*完成一個将中綴表達式轉化為字尾表達式的功能
* 具體實作步驟如下:
* (1) 1+((2+3)*4)-5 -> 1 2 3 + 4 * + 5 -
* (2) 為了便于操作,将中綴表達式字元串存儲在對應的list中(通過toInfixExpression()方法)
* 即[1,+,(,(,2,+,3,),*,4,),-,5]
* (3) 将中綴表達式對應的list =>字尾表達式
* (4) 通過字尾表達式來進行運算出結果
* */
//①中綴表達式
String expression ="1+((2+3)*4)-5";
//②将中綴表達式轉化為清單
List<String> infixExpressionList=toInfixExpression(expression);
System.out.print("中綴表達式為:");
System.out.println(infixExpressionList);
//③将中綴表達式轉化為字尾表達式
List<String> suffxiExpression=parsesuffiExpresionList(infixExpressionList);
System.out.println("字尾表達式為:"+suffxiExpression);
//④求解字尾表達式
int rbs=calculate(suffxiExpression);
//⑤輸出結果
System.out.println("計算的結果是= "+rbs);
}
/**方法:将中綴表達式轉化為對應的list*/
public static List<String> toInfixExpression(String s){
//①定義一個List,存放中綴表達式對應的内容
List<String> ls=new ArrayList<String>();
int i=0;
//指針,用來周遊中綴字元串中的字元
String str;
//完成對多位數的拼接
char c;
//将周遊到的每個字元放到 c 中
do{
//② c是一個字元,需要加入ls
if((c=s.charAt(i))<48||(c=s.charAt(i))>57){
ls.add(""+c);
i++;
}else{
/*③ 如果是一個數,還要考慮多位數*/
str="";
while(i<s.length()&&(c=s.charAt(i))>=48&&(c=s.charAt(i))<=57){
str+=c;
//拼接
i++;
}
ls.add(str);
}
}while(i<s.length());
return ls;
}
/** 方法:将中綴表達式得到的list轉化為 字尾表達式對應的List */
public static List<String> parsesuffiExpresionList(List<String> ls){
/*①定義棧
* Stack<String> s2=new Stack<String>();
* 說明:s2在裝轉化的過程中沒有pop()操作,而且到最後還要逆序輸出
* 改進:可以使用清單來代替 棧 s2
* */
Stack<String> s1=new Stack<String>();
List<String> s2=new ArrayList<String>() ;
//周遊ls
for(String item:ls){
if(item.matches("\\d+")){
s2.add(item);
}else if(item.equals("(")){
s1.push(item);
}else if(item.equals(")")){
/*處理辦法:依次彈出棧s1中的元素,并壓入s2中,直到遇到左括号為止*/
while(!(s1.peek().equals("("))){
s2.add(s1.pop());
//s1中彈出并壓入棧s2
}
s1.pop();
//将“( ”彈出
}else{
/*
*符号優先級的比較:
* 規則如下:當item的優先級小于棧s1棧頂運算符的優先級時,将s1中的棧頂運算符彈出加入到s2
* */
while(s1.size()!=0 && Operation.getValue(s1.peek()) >= Operation.getValue(item)){
s2.add(s1.pop());
}
//将item壓入棧中
s1.push(item);
}
}
//将s1中剩餘内容依次加入到s2中
while(s1.size()!=0){
s2.add(s1.pop());
}
return s2;
}
/** 方法一:将一個逆波蘭表達式依次将資料和運算符放入到ArrayList中 */
public static List<String> getListString(String suffixException) {
//将 suffixException 分割(依據“ ”)
String[] split=suffixException.split(" ");
List<String>list=new ArrayList<String>();
for(String ele:split){
list.add(ele);
}
return list;
}
/** 方法二:完成對逆波蘭表達式的運算
* 步驟如下:
* ①從左至右掃描,将3 和 4 壓入堆棧
* ②遇到 + 運算符,彈出 4 和 3 ,計算 3+4,結果為 7 存入棧中
* ③将5入棧
* ④下一個是 * 運算符,彈出 5 和 7,計算 5*7,将結果 35 存入棧中
* ⑤将6入棧
* ⑥最後一個是 - 運算符,彈出 6 和 35 ,計算 35-6,将結果29 存入棧中
* */
public static int calculate(List<String> ls) {
//(1)建立一個棧
Stack<String> stack = new Stack<String>();
//(2)周遊 ls
for (String item : ls) {
//(3)使用正規表達式來取出多位
if (item.matches("\\d+")) {
stack.push(item);
} else {
//(4)為運算符,pop出兩個數,并進行運算,然後壓入棧
int num2 = Integer.parseInt(stack.pop());
int num1 = Integer.parseInt(stack.pop());
int res = 0;
if (item.equals("+")) {
res = num1 + num2;
} else if (item.equals("-")) {
res = num1 - num2;
} else if (item.equals("*")) {
res = num1 * num2;
} else if (item.equals("/")) {
res = num1 / num2;
} else {
throw new RuntimeException("運算符有誤");
}
//将最終的運算結果壓入棧中,然後将棧頂元素彈出并轉化整型
stack.push("" + res);
}
}
return Integer.parseInt(stack.pop());
}
}
/**編寫一個類Operation 可以傳回一個運算符對應的優先級*/
class Operation{
private static int ADD=1;
private static int SUB=1;
private static int MUL=2;
private static int DIV=2;
/**寫一個方法,傳回對應的優先級數字*/
public static int getValue(String operation){
int result=0;
switch(operation){
case"+":
result=ADD;
break;
case"-":
result=SUB;
break;
case"*":
result=MUL;
break;
case"/":
result=DIV;
break;
default:
result=0;
break;
}
return result;
}
}