從01背包問題了解動态規劃---初體驗

　　01背包問題具體例子：假設現有容量10kg的背包，另外有3個物品，分别為a1，a2，a3。物品a1重量為3kg，價值為4；物品a2重量為4kg，價值為5；物品a3重量為5kg，價值為6。将哪些物品放入背包可使得背包中的總價值最大？

　　這個問題有兩種解法，動态規劃和貪婪算法。本文僅涉及動态規劃。

　　先不套用動态規劃的具體定義，試着想，碰見這種題目，怎麼解決?

　　首先想到的，一般是窮舉法，一個一個地試，對于數目小的例子适用，如果容量增大，物品增多，這種方法就無用武之地了。

　　其次，可以先把價值最大的物體放入，這已經是貪婪算法的雛形了。如果不添加某些特定條件，結果未必可行。

　　最後，就是動态規劃的思路了。先将原始問題一般化，欲求背包能夠獲得的總價值，即欲求前i個物體放入容量為m（kg）背包的最大價值c[i][m]——使用一個數組來存儲最大價值，當m取10，i取3時，即原始問題了。而前i個物體放入容量為m（kg）的背包，又可以轉化成前(i-1)個物體放入背包的問題。下面使用數學表達式描述它們兩者之間的具體關系。

　　表達式中各個符号的具體含義。

　　w[i] : 第i個物體的重量；

　　p[i] : 第i個物體的價值；

　　c[i][m] ：前i個物體放入容量為m的背包的最大價值；

　　c[i-1][m] ：前i-1個物體放入容量為m的背包的最大價值；

　　c[i-1][m-w[i]] ：前i-1個物體放入容量為m-w[i]的背包的最大價值；

　　由此可得：

　　　　　　c[i][m]=max{c[i-1][m-w[i]]+pi , c[i-1][m]}（下圖将給出更具體的解釋）

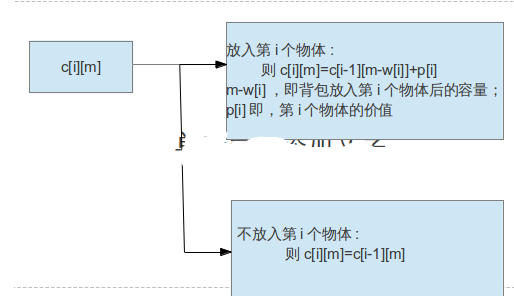
　　　　根據上式，對物體個數及背包重量進行遞推，列出一個表格（見下表），表格來自（javascript:void(0)），當逐漸推出表中每個值的大小，那個最大價值就求出來了。推導過程中，注意一點，最好逐行而非逐列開始推導，先從編号為1的那一行，推出所有c[1][m]的值，再推編号為2的那行c[2][m]的大小。這樣便于了解。

　　　　思路厘清後，開始程式設計式，C語言代碼如下所示。

#include <stdio.h>
int c[10][100]={0};

void knap(int m,int n){

    int i,j,w[10],p[10];
    for(i=1;i<n+1;i++)
        scanf("%d,%d",&w[i],&p[i]);
    for(j=0;j<m+1;j++)
        for(i=0;i<n+1;i++)
    {
        if(j<w[i])
        {
            c[i][j]=c[i-1][j];
            continue;
        }else if(c[i-1][j-w[i]]+p[i]>c[i-1][j])
            c[i][j]=c[i-1][j-w[i]]+p[i];
        else
            c[i][j]=c[i-1][j];
    }
    
}            


int main(){
    int m,n;int i,j;
    printf("input the max capacity and the number of the goods:\n");
    scanf("%d,%d",&m,&n);
    printf("Input each one(weight and value):\n");
    knap(m,n);
    printf("\n");
   for(i=0;i<=n;i++)
        for(j=0;j<=m;j++)
       {
     printf("%4d",c[i][j]);
    if(m==j) printf("\n");
    }
}

代碼中，紅色字型部分是自己寫的，其餘的參照了這篇部落格http://blog.sina.com.cn/s/blog_6dcd26b301013810.html

　　如果你很輕松地就突破了01背包，甚至很輕松地就了解了動态規劃，那麼繼續前進，做一下這道題目(http://acm.uestc.edu.cn/problem.php?pid=1012)。很好玩的。

//輸入描述:
//輸入的第 1 行，為兩個正整數，用一個空格隔開：N m
//（其中 N （ <32000 ）表示總錢數， m （ <60 ）為希望購買物品的個數。）
//
//從第 2 行到第 m + 1 行，第 j 行給出了編号為 j - 1 的物品的基本資料，每行有 3 個非負整數 v p q
//
//（其中 v 表示該物品的價格（ v<10000 ）， p 表示該物品的重要度（ 1 ~5 ）， q 表示該物品是主件還是附件。如果 q = 0 ，
//                表示該物品為主件，如果 q>0 ，表示該物品為附件， q 是所屬主件的編号）
//
//輸出描述 :
//輸出檔案隻有一個正整數，為不超過總錢數的物品的價格與重要度乘積的總和的最大值（ <200000 ）。


//動态規劃，(0,1)背包問題
#include<iostream>
using namespace std;

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

struct InputBuf
{
    int price;
    int weight;
    int type;
};

struct InputBuf inputBuf[60];
int sum_money = 0;
int sum_num = 0;

int countMaxvalue(int index, int money, int f)
{
    int a = 0, b = 0;
    if (index >= sum_num) return 0;
    if (inputBuf[index].type == 0)  //主件
    {
        if (money >= inputBuf[index].price)
        {
            a = countMaxvalue(index + 1, money - inputBuf[index].price, 1) + inputBuf[index].price * inputBuf[index].weight;  //買第index件物品的附件
            b = countMaxvalue(index + 1, money, 0);    //買主件
            return a > b ? a : b;
        }
        else
            return countMaxvalue(index + 1, money, 0);
    }
    else if ((inputBuf[index].type != 0) && (f == 1))  //附件，且主件必須買
    {
        if (money >= inputBuf[index].price)
        {
            a = countMaxvalue(index + 1, money - inputBuf[index].price, f) + inputBuf[index].price * inputBuf[index].weight;
            b = countMaxvalue(index + 1, money, f);
            return a > b ? a : b;
        }
    }
    else
    {
        return countMaxvalue(index + 1, money, f);
    }
    return 0;
}



int main(void)
{
    int i = 0;
    scanf("%d %d", &sum_money, &sum_num);
    for (i = 0; i < sum_num; i++)
    {
        scanf("%d %d %d", &inputBuf[i].price, &inputBuf[i].weight, &inputBuf[i].type);
    }
    printf("%d", countMaxvalue(0, sum_money, 1));
    return 0;
}

C/C++基本文法學習

STL

C++ primer

#include <stdio.h>
int c[10][100]={0};

void knap(int m,int n){

    int i,j,w[10],p[10];
    for(i=1;i<n+1;i++)
        scanf("%d,%d",&w[i],&p[i]);
    for(j=0;j<m+1;j++)
        for(i=0;i<n+1;i++)
    {
        if(j<w[i])
        {
            c[i][j]=c[i-1][j];
            continue;
        }else if(c[i-1][j-w[i]]+p[i]>c[i-1][j])
            c[i][j]=c[i-1][j-w[i]]+p[i];
        else
            c[i][j]=c[i-1][j];
    }
    
}            


int main(){
    int m,n;int i,j;
    printf("input the max capacity and the number of the goods:\n");
    scanf("%d,%d",&m,&n);
    printf("Input each one(weight and value):\n");
    knap(m,n);
    printf("\n");
   for(i=0;i<=n;i++)
        for(j=0;j<=m;j++)
       {
     printf("%4d",c[i][j]);
    if(m==j) printf("\n");
    }
}

代碼中，紅色字型部分是自己寫的，其餘的參照了這篇部落格http://blog.sina.com.cn/s/blog_6dcd26b301013810.html

//輸入描述:
//輸入的第 1 行，為兩個正整數，用一個空格隔開：N m
//（其中 N （ <32000 ）表示總錢數， m （ <60 ）為希望購買物品的個數。）
//
//從第 2 行到第 m + 1 行，第 j 行給出了編号為 j - 1 的物品的基本資料，每行有 3 個非負整數 v p q
//
//（其中 v 表示該物品的價格（ v<10000 ）， p 表示該物品的重要度（ 1 ~5 ）， q 表示該物品是主件還是附件。如果 q = 0 ，
//                表示該物品為主件，如果 q>0 ，表示該物品為附件， q 是所屬主件的編号）
//
//輸出描述 :
//輸出檔案隻有一個正整數，為不超過總錢數的物品的價格與重要度乘積的總和的最大值（ <200000 ）。


//動态規劃，(0,1)背包問題
#include<iostream>
using namespace std;

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

struct InputBuf
{
    int price;
    int weight;
    int type;
};

struct InputBuf inputBuf[60];
int sum_money = 0;
int sum_num = 0;

int countMaxvalue(int index, int money, int f)
{
    int a = 0, b = 0;
    if (index >= sum_num) return 0;
    if (inputBuf[index].type == 0)  //主件
    {
        if (money >= inputBuf[index].price)
        {
            a = countMaxvalue(index + 1, money - inputBuf[index].price, 1) + inputBuf[index].price * inputBuf[index].weight;  //買第index件物品的附件
            b = countMaxvalue(index + 1, money, 0);    //買主件
            return a > b ? a : b;
        }
        else
            return countMaxvalue(index + 1, money, 0);
    }
    else if ((inputBuf[index].type != 0) && (f == 1))  //附件，且主件必須買
    {
        if (money >= inputBuf[index].price)
        {
            a = countMaxvalue(index + 1, money - inputBuf[index].price, f) + inputBuf[index].price * inputBuf[index].weight;
            b = countMaxvalue(index + 1, money, f);
            return a > b ? a : b;
        }
    }
    else
    {
        return countMaxvalue(index + 1, money, f);
    }
    return 0;
}



int main(void)
{
    int i = 0;
    scanf("%d %d", &sum_money, &sum_num);
    for (i = 0; i < sum_num; i++)
    {
        scanf("%d %d %d", &inputBuf[i].price, &inputBuf[i].weight, &inputBuf[i].type);
    }
    printf("%d", countMaxvalue(0, sum_money, 1));
    return 0;
}

從01背包問題了解動态規劃---初體驗

繼續閱讀

UVA 590 Always on the run

FZU 1978 Repair the brackets

UVA 10344- 23 out of 5

ZOJ 3935 2016

POJ 2115 C Looooops

HDU 5381 The sum of gcd

ZOJ 1104 Leaps Tall Buildings

ZOJ 3700 Ever Dream

HDU 2821 Pusher

ZOJ 1199 Point of Intersection

UVA 1401 Remember the Word

UVA 620 Cellular Structure

ZOJ 2748 Free Kick

CSU 1567 Reverse Rot

UVA 519 Puzzle (II)

HDU 1160 FatMouse's Speed （記錄路徑的最長上升子序列）