在《機器學習---文本特征提取之詞袋模型(Machine Learning Text Feature Extraction Bag of Words)》一文中,我們通過計算文本特征向量之間的歐氏距離,了解到各個文本之間的相似程度。當然,還有其他很多相似度度量方式,比如說餘弦相似度。
在《皮爾遜相關系數與餘弦相似度(Pearson Correlation Coefficient & Cosine Similarity)》一文中簡要地介紹了餘弦相似度。是以這裡,我們比較一下歐氏距離和餘弦相似度之間的差別。
首先來說一下歐氏距離(Euclidean Distance):
n維空間裡兩個向量X(x1,x2,…,xn)與Y(y1,y2,…,yn)之間的歐氏距離計算公式是:
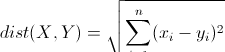
用矩陣表示法表示為:
再來說一下餘弦相似度(Cosine Similarity):
n維空間裡兩個向量x(x1,x2,…,xn)與y(y1,y2,…,yn)之間的餘弦相似度計算公式是:
用向量形式表示為:
相同之處:
在機器學習中都可以用來計算相似程度。歐氏距離是最常見的距離度量,而餘弦相似度則是最常見的相似度度量。很多其他的距離度量和相似度度量都是基于這兩者的變形和衍生。
差別:
借助三維坐标系來看下歐氏距離和餘弦相似度的差別。(下圖摘自:https://blog.csdn.net/lin00jian/article/details/51209715)
從圖上可以看出歐式距離衡量的是空間中各點之間的絕對距離,和點所在的位置坐标(即個體各次元的特征數值)直接相關,距離越小,兩向量之間越相似;而餘弦相似度衡量的是空間中兩向量之間的夾角,展現的是方向上的差異,夾角越小(餘弦相似度越大),兩向量之間越相似。如果保持A點的位置不變,B點朝原方向延伸,那麼這個時候餘弦相似度cosθ是保持不變的,因為夾角不變,而A、B兩點間的距離顯然在發生改變,這就是歐氏距離和餘弦相似度的不同之處。
适用場景:
歐氏距離能夠展現個體數值特征的絕對差異,是以更多的用于需要從次元的數值大小中展現差異的分析,比如使用使用者行為作為名額分析使用者價值的相似情況(比較不同使用者的消費能力),這屬于價值度量;而餘弦相似度對絕對數值不敏感,更多的用于使用使用者對内容的評分來分析使用者興趣的相似程度(使用者是否喜歡某商品),這屬于定性度量。
需要注意的是,歐氏距離和餘弦相似度都需要保證各次元處于相同的刻度級别(量綱),是以一般需要對資料先進行标準化處理,否則很可能會引起偏差。比如使用者對内容評分,假設為5分制,對使用者甲來說評分3分以上就是自己喜歡的,而對于使用者乙,評分4分以上才是自己喜歡的,這樣就無法很好地衡量兩個使用者評分之間的相似程度。如果将評分數值減去平均值,那麼就可以很好地解決問題。此時,就相當于用皮爾遜相關系數來度量相似程度。