一.簡介:
平衡二叉樹(Self-Balcncing Binary Search Tree 或 Height-Balanced Binary Search Tree)是一種特殊的二叉排序樹,其中每一個結點的左子樹和右子樹的高度差至多等于1.
二叉樹适用于在存儲時需要保持有序的結構.平衡二叉樹是一種優化的二叉樹,平衡的作用是降低樹的深度,這樣能有效降低查找時的次數.
在二叉樹中,可以将結點左子樹深度和右子樹深度的內插補點成為平衡因子(Balance Factor),二叉樹所有結點的平衡因子隻能是0或±1.
二.平衡二叉樹的實作原理:
1.左旋和右旋操作
二叉樹要想實作平衡,在每一次插入結點或移除結點時都需要判斷這一操作是否導緻了二叉樹不平衡,如果不平衡需要移動結點的位置重新平衡二叉樹.具體來說,我們通過計算結點的平衡因子來确定是否需要進行平衡,平衡的過程有兩種,一種是當平衡因子大于1時需要左旋轉,一種是平衡因子小于-1時需要進行右旋轉.我們以下圖的樹為例:
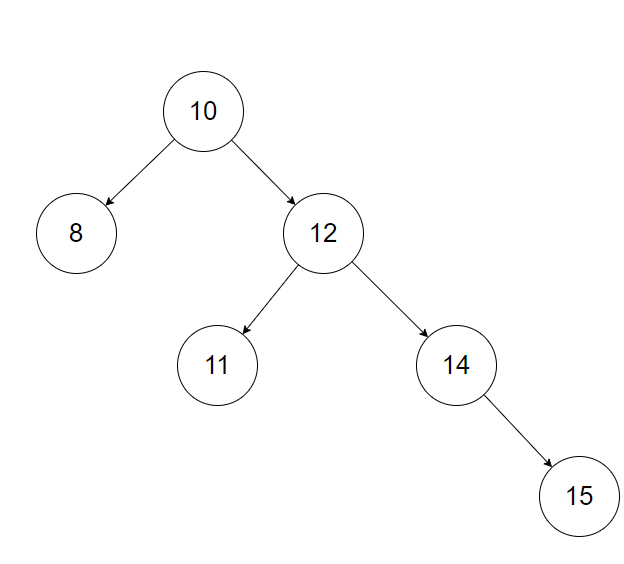
總結一下:左旋操作包括以下幾步:1)使目前結點的右子結點的左子結點指向目前結點(将右子結點12上拉,目前結點10下壓);2)讓目前結點的右子結點指向上一步操作前目前結點右子結點的左子結點(将結點11重新挂回二叉排序樹);3)如果進行左旋的這部分結點有父節點,還需要更改父節點的指向.
結點的右旋操作就不再重複說明,和左旋操作完全相反.
2.左旋和右旋的時機
上面左旋和右旋的過程中已經有說明,當某個結點的平衡因子的絕對值大于1時需要在這個結點上進行左旋或右旋,根據平衡因子的定義,當平衡因子大于1時說明左子樹深度大于右子樹深度(左重右輕),需要進行右旋,當平衡因子小于-1時說明右子樹深度大于左子樹深度(左輕右重),需要進行左旋.但是下面一種情況卻需要特别指出,如下圖所示:
我們重新計算平衡因子會發現16結點的平衡因子又變成了2,仍然沒有解決問題.那這是怎麼一回事呢?
對比兩次旋轉前的平衡因子的值我們發現,第一次旋轉10結點和12結點的平衡因子都為負數,代表它們都是左輕右重的,而第二次旋轉時12結點和16結點的平衡因子一正一負,代表它們一個左輕右重一個左重右輕.我們細細品味一下左旋的過程,會發現在左旋的過程中進行左旋的兩個結點的平衡因子都會變大,以第一次旋轉為例,10結點的左子樹雖然沒有變化,但是右子樹從12變為了11,顯然旋轉前10結點的右子樹深度值至少是11結點深度值加1,旋轉後10結點右子樹深度值就是11結點深度值,是以右子樹深度值一定變小;12結點的左子樹原來是11結點,旋轉後11結點是10結點的右子樹,由于旋轉後10結點的深度值至少是11結點深度值加1,是以12結點的左子樹的深度值一定變大,是以綜合來看10結點和12結點的平衡因子都應該變大了.是以也就不難解釋為什麼這次的左旋沒有讓樹重新平衡了,因為這次左旋前作左旋操作的12結點和16結點的平衡因子一正一負,是以當左旋後它們的平衡因子都變大後,原來平衡因子為正的16結點的平衡因子就會大于1.是以我們在進行左旋前一定要保證進行左旋的兩個結點的平衡因子都不為正.那麼對于第二種情況我們應該怎麼辦呢?很簡單,我們先對平衡因子為正的16結點和13結點一起進行一次右旋操作讓13結點變成12結點的右子結點,13結點的平衡因子減小了一定不為正,這時就可以把12結點和13結點一起進行左旋操作了,最終的結果如下圖所示:
/************************************
* 建立人:movin
* 建立時間:2021/7/26 21:06:11
* 版權所有:個人
***********************************/
using System;
using System.Collections.Generic;
using System.Text;
namespace SearchCore
{
/// <summary>
/// AVL樹結點
/// </summary>
public class AVLNode
{
/// <summary>
/// 結點中存儲的資料,資料可根據需要修改
/// </summary>
public int Content { get; set; }
/// <summary>
/// 平衡因子
/// </summary>
public int BalanceFactor { get; private set; }
/// <summary>
/// 左子樹深度值
/// </summary>
public int LeftChildDegree { get; private set; }
/// <summary>
/// 右子樹深度值
/// </summary>
public int RightChildDegree { get; private set; }
/// <summary>
/// 左子樹根結點
/// </summary>
public AVLNode LeftChild { get; set; }
/// <summary>
/// 右子樹根結點
/// </summary>
public AVLNode RightChild { get; set; }
public AVLNode(int content)
{
Content = content;
}
/// <summary>
/// 右旋方法
/// </summary>
private void RightRotate(AVLNode parent,ref AVLNode root)
{
//将左子樹暫存起來,不用校驗左子樹是否為空,因為觸發右旋時平衡因子一定大于0,左子樹不可能為空
var temp = LeftChild;
//将目前結點的左子樹的右子樹置為目前結點的左子樹
LeftChild = temp.RightChild;
//目前結點變為目前結點原左子樹的右子樹
temp.RightChild = this;
//改變父節點的指針指向
if(parent != null)
{
if(parent.LeftChild == this)
{
parent.LeftChild = temp;
}
else if(parent.RightChild == this)
{
parent.RightChild = temp;
}
}
else
{
root = temp;
}
}
/// <summary>
/// 左旋方法
/// </summary>
/// <param name="parent"></param>
private void LeftRotate(AVLNode parent,ref AVLNode root)
{
//将右子結點暫存起來
var temp = RightChild;
//将目前結點的右子樹的左子樹置為目前結點的右子樹
RightChild = temp.LeftChild;
//目前結點置為目前結點原右子樹的左子樹
temp.LeftChild = this;
//改變父節點的指針指向
if (parent != null)
{
if (parent.LeftChild == this)
{
parent.LeftChild = temp;
}
else if (parent.RightChild == this)
{
parent.RightChild = temp;
}
}
else
{
root = temp;
}
}
/// <summary>
/// 添加子結點
/// </summary>
/// <param name="content"></param>
public AVLNode AddChildNode(int content,AVLNode parent,ref AVLNode root)
{
AVLNode result = null;
if (content < Content)
{
if (LeftChild == null)
{
LeftChild = new AVLNode(content);
result = LeftChild;
}
else
{
result = LeftChild.AddChildNode(content,this,ref root);
}
}
else if (content > Content)
{
if (RightChild == null)
{
RightChild = new AVLNode(content);
result = RightChild;
}
else
{
result = RightChild.AddChildNode(content,this,ref root);
}
}
//如果添加到了目前對象的子對象中,則需要重置左右子樹的深度值并計算檢驗平衡因子絕對值是否大于1
if (result != null)
{
CalcAndCheckBalanceFactor(parent,ref root);
}
return result;
}
/// <summary>
/// 計算并檢驗平衡因子
/// </summary>
public void CalcAndCheckBalanceFactor(AVLNode parent,ref AVLNode root)
{
//左子樹深度值取左子樹的左右子樹深度值中的最大值加一
LeftChildDegree = LeftChild == null ? 0 : (Math.Max(LeftChild.LeftChildDegree, LeftChild.RightChildDegree) + 1);
RightChildDegree = RightChild == null ? 0 : (Math.Max(RightChild.LeftChildDegree, RightChild.RightChildDegree) + 1);
//計算平衡因子
BalanceFactor = LeftChildDegree - RightChildDegree;
//計算完平衡因子後馬上檢驗平衡因子的絕對值
if (BalanceFactor > 1)
{
if (LeftChild.BalanceFactor < 0)
{
LeftChild.ReLeftBalance(this,ref root);
}
ReRightBalance(parent,ref root);
}
else if (BalanceFactor < -1)
{
if (RightChild.BalanceFactor > 0)
{
RightChild.ReRightBalance(this,ref root);
}
ReLeftBalance(parent,ref root);
}
}
/// <summary>
/// 重新左平衡(作左旋)
/// </summary>
public void ReLeftBalance(AVLNode parent,ref AVLNode root)
{
//臨時記錄目前結點的左子結點
var temp = LeftChild;
LeftRotate(parent,ref root);
//左旋會引起旋轉前目前結點和目前結點的左子結點的平衡因子變化,需要重新計算平衡因子
//注意計算順序
CalcAndCheckBalanceFactor(temp,ref root);
if(temp != null)
{
temp.CalcAndCheckBalanceFactor(parent,ref root);
}
}
/// <summary>
/// 重新右平衡(作右旋)
/// </summary>
public void ReRightBalance(AVLNode parent,ref AVLNode root)
{
//臨時記錄目前結點的右子結點
var temp = RightChild;
RightRotate(parent,ref root);
//左旋會引起旋轉前目前結點和目前結點的左子結點的平衡因子變化,需要重新計算平衡因子
//注意計算順序
CalcAndCheckBalanceFactor(temp,ref root);
if(temp != null)
{
temp.CalcAndCheckBalanceFactor(parent,ref root);
}
}
}
} /************************************
* 建立人:movin
* 建立時間:2021/7/26 21:11:28
* 版權所有:個人
***********************************/
using System;
using System.Collections.Generic;
using System.Text;
namespace SearchCore
{
/// <summary>
/// AVL樹結構
/// </summary>
public class AVLTree
{
private AVLNode root;
/// <summary>
/// 根結點
/// </summary>
public AVLNode Root
{
get
{
return root;
}
}
/// <summary>
/// 插入新的結點
/// </summary>
/// <param name="content"></param>
public AVLNode InsertAVLNode(int content)
{
if(root == null)
{
root = new AVLNode(content);
return root;
}
return Root.AddChildNode(content,null,ref root);
}
}
}