大家好!
動态規劃題目是總結的比較完整了。下面是自從和大家刷開題總結的動态規劃解題方法。
今年全國夏天雨是真的多,突然想到今年北京的夏天也不像往年那麼熱。不知不覺就穩穩地度過了夏天來到秋天。
恰巧前幾天有一個粉絲問到了我,網上接雨水的解決總是感覺有點混亂,能不能用動态規劃解決。
今早北京大雨,借用大雨的感受,想了想接雨水問題,依然用長圖一步一步說明!
背景
先來看看題目,這個題目應該是很多人都已經遇到過了,因為它的題号是42,屬于一個比較非常靠前的題目。
同時也屬于一個非常經典的算法問題。
咱們今天的題目解決不做暴力法、也不做雙指針,就用動态規劃很清晰的進行說明。
看下圖,12根柱子的圍欄,接了6個機關的雨水。
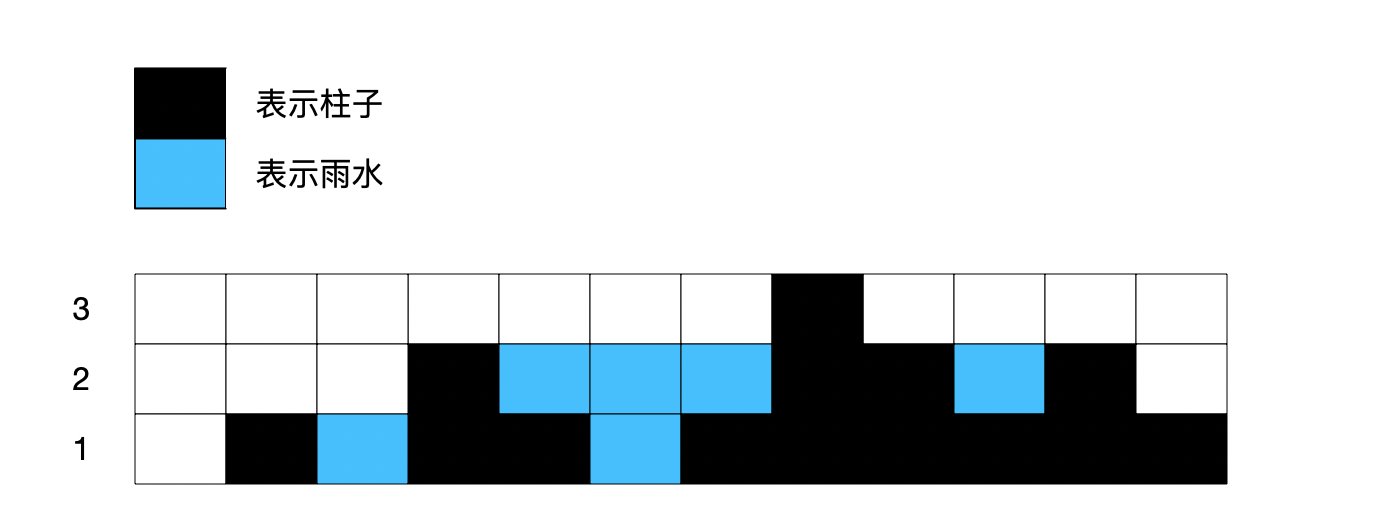
從上圖很顯然能看到一點:
如果想要接住雨水。那麼,決定雨量的多少在于「左邊的柱子高度」、「右邊的柱子高度」以及「自身柱子的高度」。
比如說,中間第 5 格雨水量為2,就是決定于左右側柱子的較小值-本身柱子高度(0)而得到的。
注意:左右側的高度,指的是能圍住雨水的柱子,而不是緊挨着的左右側的柱子。
左側最高柱子:2
右側最高柱子:3
自身柱子高度:0
雨水量 = min(左側最高柱子, 右側最高柱子) - 自身柱子高度 = 2
是以,需要定義兩個數組,分别來存放相對于目前位置左側和右側柱子的最大高度。
最後,取左右側柱子最小值-自身柱子高度=雨水量。
思路
就用leetcode官方給的案例來進行一步一步解決。
柱子高度為:height = [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1],再把圖拿過來!
現在,定義兩個數組,分别命名為
left_max_height
和
right_max_height
,存放相對于目前位置左側和右側柱子的最大高度。
先來定義第一個數組
left_max_height
,存放左側最高柱子高度:
初始化:(因為左側沒有柱子,是以位置 0 左側最大高度為 0)
left_max_height[0] = 0 動态方程:
left_max_height[i]=max(height[i-1], left_max_height[i-1]) 下面還是用長圖一步一步來進行說明:【點選高清顯示】
下面開始定義第二個數組,存放右側最高柱子高度。右側最高度從最右側開始進行計算。
初始化:(因為最後一個位置由側沒有柱子,是以位置 11 右側最大高度為 0)
right_max_height[11] = 0 right_max_height[j]=max(height[j+1], right_max_height[j+1]) 還是用長圖一步一步來進行說明:【點選高清顯示】
現在,目前位置的左側和右側柱子的最大高度數組計算完成後,下面就計算接水量。
準備好三個數組:
上圖中,height = [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1],為了看起來清晰,可以參考最開始圖示。
最大機關水量=左右取最小值-本身的高度
計算方式:
water=min(left_max_height[i], right_max_height[i])-height[i])
max_water=water>=0?water:0 上述需要注意一點,如果
左右取最小值-本身的高度<0
,說明目前本身柱子是凸出來左右側最高值的,比如說位置 1:
是以說,位置 1 的計算結果為負數,需要強制轉為 0。
##代碼
class Solution(object):
def trap(self, height):
size = len(height)
# 小于等于 2 的時候,是接不住雨水的
if size <= 2:
return 0
# 左邊相對于目前位置的最大高度
left_max_height = [0 for _ in range(size)]
# 右邊相對于目前位置的最大高度
right_max_height = [0 for _ in range(size)]
# 目前位置接雨水最大高度
max_water = [0 for _ in range(size)]
# 初始化 left_max_height, 第 0 個位置初始化為 0
for i in range(1, size):
left_max_height[i] = max(height[i-1], left_max_height[i-1])
# 初始化 right_max_height, 第 size-1 個位置初始化為 0
for j in range(1, size):
right_max_height[size-j-1] = max(height[size-j], right_max_height[size-j])
# 最大水量
for k in range(1, size):
max_water[k] = (min(left_max_height[k], right_max_height[k])-height[k] if min(left_max_height[k], right_max_height[k])-height[k]>=0 else 0)
# 累計求機關水量
waters = 0
for z in range(1, size):
waters += max_water[z]
return waters
if __name__ == '__main__':
s = Solution()
print(s.trap([0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1])) 這個題目總體來說,使用動态規劃還是不容易想到的。尤其是上面兩個數組使用了兩次動态規劃的過程。
接雨水問題還可以使用暴力解法和雙指針解決,雙指針可以試試,至于暴力。。心裡有就好了哈哈。。
多餘的一句
邊工作邊帶大家刷題确實是有點慢了,很抱歉!