先回顧之前的三篇文章
“算法實踐——數獨的基本解法”,介紹求解數獨的基本的暴力搜尋法
“跳躍的舞者,舞蹈鍊(Dancing Links)算法——求解精确覆寫問題”,網友huangfeidian介紹的求解數獨的舞蹈鍊(Dancing Links)算法,這篇文章是介紹舞蹈鍊(Dancing Links)算法的。
“算法實踐——舞蹈鍊(Dancing Links)算法求解數獨”,該文介紹了用舞蹈鍊(Dancing Links)算法求解數獨,并給出了暴力破解法和舞蹈鍊(Dancing Links)算法之間的時間和空間占用效率的對比。
撇開空間占用的效率不談,在前文中有下面的時間效率的資料對比
暴力破解法的效率
數獨一:0.114毫秒
數獨二:0.238毫秒
數獨三:15.706毫秒
數獨的舞蹈鍊(Sudoku Dancing Links)算法的效率
數獨一:1.31毫秒
數獨二:2.81毫秒
數獨三:5.56毫秒
數獨的舞蹈鍊(Sudoku Dancing Links)算法在數獨一和數獨二上不占優勢,但是在數獨三上的時間效率領先不止一點點
那是為何呢?通過分析三個數獨可知,在暴力破解法中,數獨一沒有緩存資料,一路唯一數單元格到底;數獨二緩存了12步資料;數獨三緩存了21步資料;
于是做了推測,數獨的舞蹈鍊(Sudoku Dancing Links)算法在緩存上優勢,但是在構造數獨矩陣的時候耗費了大量的時間。數獨的緩存越多,該算法就越有優勢,直到時間效率完全超越暴力破解法
在前文中也提到,數獨的舞蹈鍊(Sudoku Dancing Links)算法本質上也是暴力破解法,隻是采用了獨特的資料結構,使得效率提升。于是針對數獨三,把暴力破解法和數獨的舞蹈鍊(Sudoku Dancing Links)算法的求解的前十步貼出來比較一下
先把數獨三貼出來
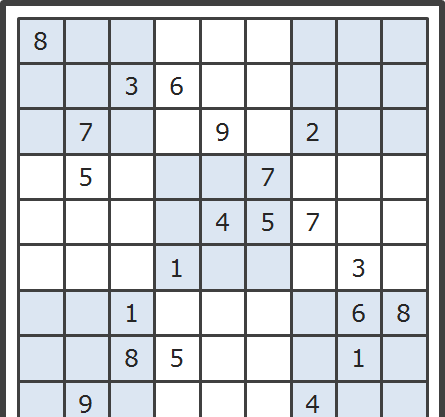
暴力破解法的前十步
1、緩存1,在(8,7)填數,2種可能(3或9)。先填3
2、緩存2,在(7,7)填數,2種可能(5或9)。先填5
3、緩存3,在(9,8)填數,2種可能(2或7)。先填2
4、在(9,9)填數,1種可能。填7
5、在(8,9)填數,1種可能。填9
6、緩存4,在(9,3)填數,2種可能(5或6)。先填6
7、緩存5,在(3,3)填數,2種可能(4或6)。先填6
8、緩存6,在(2,2)填數,2種可能(1或2)。先填1
9、緩存7,在(1,2)填數,2種可能(2或6)。先填2
10、緩存8,在(1,3)填數,2種可能(6或9)。先填6
可以看出暴力破解法的前十步中,有八步是緩存資料(每一步都有2種可能)。
數獨的舞蹈鍊(Sudoku Dancing Links)算法的前十步
3、第6行填5,1種可能(在第9列),在(6,9)填5
4、第9宮填9,1種可能(在第8行、第9列),在(8,9)填9
5、緩存3,在(9,8)填數,2種可能(2或7)。先填2
6、在(9,9)填數,1種可能。填7
7、第3列填7,1種可能(在第6行),在(6,3)填7
8、緩存4,在(2,9)填數,2種可能(1或4)。先填1
9、第7列填1,1種可能(在第4行),在(4,7)填1
10、緩存5,在(1,7)填數,2種可能(6或9)。先填6
和暴力破解法的前十步相比,緩存資料的步數減少(有五步),增加了對行、列、宮填數的唯一性的判斷。
例如:第3步中,當時第6行中能填5的格子,隻有(6,9),雖然(6,9)中能填的數是2、4、5、6、9這5個數。那麼隻能在(6,9)中填5。減少了後續的計算可能。同理,第4步、第7步、第9步也是同樣的道理
從這點看,由于數獨的舞蹈鍊(Sudoku Dancing Links)算法增加了對行、列、宮填數的唯一性的判斷,使得總步數大大減少,進而提高了時間效率。
那為何數獨一和數獨二不占時間優勢呢?數獨一一路唯一數單元格到底,不需要對行、列、宮填數的唯一性的判斷。數獨二,緩存的步數比較少,對行、列、宮填數的唯一性的判斷雖然能減少步數,但可能不明顯,加上其在構造數獨矩陣上耗費了時間,是以總的時間損耗比較大,也就不占優勢了。
那如果在暴力破解法中,增加對行、列、宮填數的唯一性的判斷。是不是能提高求解的效率呢?
先增加下面的一個函數,對行、列、宮填數的唯一性的判斷,如果有滿足條件的唯一數,則傳回坐标和數(組合,坐标*10+數),否則傳回-1,其中P(K) = IIf(P(K) = -1, I * 9 + J, -2)是個條件判斷,當P(K)=-1時,說明之前沒有滿足的條件,把P(K)設定成坐标值;當P(K)=-1時,說明之前有滿足的條件,把P(K)設定成-2。然後一個循環判斷P(K)值有沒有大于-1(大于等于0)的,有說明有唯一數,傳回坐标和數
Private Function GetOnly() As Integer
Dim I As Integer, J As Integer, K As Integer
Dim P(8) As Integer
'row
For I = 0 To 8
For K = 0 To 8
P(K) = -1
Next
For J = 0 To 8
If _Num(I * 9 + J) > 0 Then
For K = 0 To 8
If (_Num(I * 9 + J) And _V(K)) = _V(K) Then
P(K) = IIf(P(K) = -1, I * 9 + J, -2)
End If
Next
End If
If P(K) >= 0 Then Return P(K) * 10 + K
Next
'col
If _Num(J * 9 + I) > 0 Then
If (_Num(J * 9 + I) And _V(K)) = _V(K) Then
P(K) = IIf(P(K) = -1, J * 9 + I, -2)
'mat
Dim S As Integer
S = (Int(I / 3) * 3 + Int(J / 3)) * 9 + (I Mod 3) * 3 + (J Mod 3)
If _Num(S) > 0 Then
If (_Num(S) And _V(K)) = _V(K) Then
P(K) = IIf(P(K) = -1, S, -2)
If P(K) >= 0 Then Return P(K) * 10 + K
Return -1
End Function
然後在FindMinCell函數中增加對行、列、宮填數的唯一性的判斷,下面代碼中紅色的部分。但tP不等于-1時,說明此時沒有唯一數單元格,那麼判斷有沒有行、列、宮的唯一數。若有,則填數,并繼續找尋唯一數單元格等;若沒有,傳回可選數最少的單元格
Private Function FindMinCell() As Integer
Dim I As Integer, C As Integer
Dim tP As Integer = -1, tMin As Integer = 20
I = 0
Do
Do
If _Num(I) > 0 Then
C = Get1Count(_Num(I))
If C = 1 Then
If SetNumPri(I, _Num(I)) = False Then Return -2
If I = tP Then
tP = -1
tMin = 20
I = -1
Else
If C < tMin Then
tP = I
tMin = C
End If
I += 1
Loop Until I > 80
If tP = -1 Then Return -1
S = GetOnly()
If S > 0 Then
Dim S2 As Integer = Int(S / 10)
Dim S3 As Integer = S Mod 10
If SetNumPri(S2, _V(S3)) = False Then Return -2
I = 0
tP = -1
tMin = 20
End If
Loop Until I > 80
Return tP
我把它稱之為改良的暴力破解法,下面看看三個算法對求解數獨的時間效率的對比(從新測定,資料和之前的有偏差,和電腦運作時狀态有關)
暴力破解法
數獨一:0.113毫秒
數獨二:0.240毫秒
數獨三:15.555毫秒
數獨的舞蹈鍊(Sudoku Dancing Links)算法
數獨一:6.323毫秒
數獨二:8.484毫秒
數獨三:11.239毫秒
改良的暴力破解法
數獨二:0.837毫秒
數獨三:11.324毫秒
從上面的資料可以看出,改良的暴力破解法在數獨一和數獨三上基本上都到了三者最優的狀态。在數獨二上沒有展現優勢,推測問題出在數獨二上行、列、宮的唯一數可能性比較少,但為此耗費了不少的計算時間。
把改良的暴力破解法和暴力破解法的求解數獨三過程儲存到檔案分析了一下,改良的暴力破解法的檔案的大小是暴力破解法的20%左右,說明改良的暴力破解法大大縮小了求解的步數,也就是提高了求解的時間效率。
還能不能改良?在本文中,在沒有唯一數單元格時,再求解行、列、宮的唯一數的過程,那麼這裡面有很多的重複計算。能不能在每次填數的時候,都把行、列、宮的可填性更新,這樣在求解行、列、宮的唯一數的過程中就不需要重新計算了。我試了一下,一是空間占用成本高,需要額外的243位元組存儲行、列、宮的可填性,每次緩存的時候,這243位元組也要緩存,增加緩存的負擔。二是每次填數的時候,更新行、列、宮的可填性的計算比較複雜,需要耗費比較多的計算時間。三是在數獨一和數獨二的情況下,對行、列、宮的可填性依賴不大,更新行、列、宮的可填性的計算反而是做了很多的無用功(尤其是數獨一,根本不需要對行、列、宮的可填性的判斷),耗費計算時間,降低時間效率。
如果網友中還有什麼其他比較好的數獨的求解方法,望不吝賜教,大家互相交流,共同提高。
作者:萬倉一黍
出處:http://grenet.cnblogs.com/
本文版權歸作者和部落格園共有,歡迎轉載,但未經作者同意必須保留此段聲明,且在文章頁面明顯位置給出原文連接配接,否則保留追究法律責任的權利。